
- •1 Вопрос
- •3. Механический смысл производной. Мгновенная скорость. Ускорение
- •1. Достаточное условие возрастания и убывания функции.
- •10. Понятие дифференциала
- •1 2. Вогнутость, выпуклость, точки перегиба
- •14. Асимптоты кривых. Правило нахождение асимптот
- •16 Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке
- •17. Первообразная и неопределённый интеграл.
- •18 Таблица интегралов.
- •19.Свойства неопределенного интеграла.
- •21) Метод замены переменной для неопределенного интеграла.
- •25.Определенный интеграл
- •27. Свойства определенного интеграла
- •28. Формула Ньютона- Лейбница.
- •29)Замена переменной и формула интегрирования по частям для определенного интеграла.
- •30 Вычисление площадей плоских фигур
- •32.Теория вероятности. Случайные события.
- •34.Теория сложения и умножения вероятностей.
- •36. Закон распределение дискретной случайной велечины.
- •37. Математическое ожидание дискретной случайной величины и его свойства.
- •39. Непрерывные случайные величины. Функция распределения. Плотность вероятности.
- •40. Равномерное распределение
- •41. Показательное распределение
- •Вопрос 43.
- •44. Статистическое распределение выборки. Полигон и гистограмма
- •46. Определение интервальной оценки
- •48. Проверка гипотезы о нормальном распределении.
21) Метод замены переменной для неопределенного интеграла.
Рассмотрим неопределенный интеграл F(x) некоторой функции f(x). Для упрощения вычисления интеграла часто удобно выполнить замену переменной. Переход от x к новой переменной u описывается выражением
![]()
где x = g (u) - подстановка. Соответственно, обратная функция u = g −1(x) описывает зависимость новой переменной от старой.
Пример 1.
Вычислить:
![]()
Решение.
Сделаем
замену .
![]() Тогда .
Тогда .
![]() Следовательно, интеграл принимает вид
:
Следовательно, интеграл принимает вид
:

25.Определенный интеграл
Понятие определенного интеграла
y=f(x) [a;b]
«Кси» (ξ) — буква греческого алфавита.
Ξ ξ:€
[ x i-1
; x i
]
, где
i=1,2…n
ξ:€
[ x i-1
; x i
]
, где
i=1,2…n
Y
F(ξ3)
F(ξ2)
F(ξ1)

X0 X1 X2 Xn X
ξ1 ξ 2 ξ3
Сумма вида
n |
∑ i=1 |
f(ξk) · Δxk , - интегральная сумма y=f(x) на отрезке [a;b]
к аждое
слагаемое в интегральной сумме
аждое
слагаемое в интегральной сумме
f(ξk) · Δxk равно площади в прямоугольного со сторонами f(ξk) и Δxk наибольший из отрезков [ x i-x ; xi ]
о бозначим
max
x
вся интегральная сумма будет равна
бозначим
max
x
вся интегральная сумма будет равна
n
S= ∑ Si
i=1
Если существует конечный предел интегральной суммы при мах х à 0,
не зависящий от способа разбиения отрезка [a;b] и выбора точек ξi, то этот предел называется определенным интегралом от функции y=f(x) на отрезке [a;b]

n |
∑ i=1 |
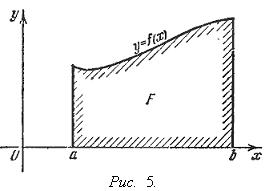
26 Геометрический смысл определенного интеграла. Если f(x) непрерывна и положительна на [a, b], то интеграл
![]()
![]()
представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f(x) (см. рис. 5.).
Не следует думать, что условие непрерывности функции необходимо для того, чтобы у нее существовал определенный интеграл. Интеграл может существовать и у разрывной функции. Пусть, например, функцияf(x), заданная на промежутке [a, b], равна нулю во всех точках этого промежутка, кроме конечного числа точек z1, z2, ..., zN. Составим для f(x) интегральную сумму σ.
Пусть из точек ξ0, ξ1, ..., ξn-1, входящих в определение σ, p точек совпадают с точками zi, а остальные отличны от них. Тогда в сумме σ будет лишь p слагаемых, отличных от нуля. Если наибольшее из чисел |f(zi) | (i = 1, 2, ..., N) есть K, то, очевидно,
| σ | ≤ Kpλ ≤ KNλ,
откуда ясно, что при λ → 0 будет и σ → 0. Таким образом, интеграл
существует и равен нулю.
Приведем теперь пример функции, не имеющей интеграла. Пусть φ(x) задана на промежутке [0, 1] так:

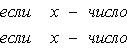

Если мы, составляя сумму σ, за точки ξk выберем числа иррациональные, то окажется σ = 0. Если же все ξkвзять рациональными, то получится σ = 1. Таким образом, за счет одного лишь уменьшения λ нельзя приблизить σ к какому-либо постоянному числу, и интеграл
![]()
![]()
не существует.
В настоящее время известны точные признаки, позволяющие судить, имеет или нет заданная функция определенный интеграл, но мы ограничимся вышеприведенной теоремой об интегрируемости непрерывных функций.
