Многочлены.

Комплексное число z₀ называется корнем многочлена P(z), если P(z₀)=0.

Теорема Безу. Число z₀ ,будет корнем многочлена P(z) степени n>=1, тогда и только тогда, когда P(z) делится на (z-z₀) без остатка.

Док-во. P(z)=H(z)(z-z₀)+R(z), где H(z) – многочлен степени (n-1), а остаток R(z) – многочлен степени 1, т.е. degR=0, т.е. R(z)=C. Итак, P(z)=(z- z₀)H(z)+C;

z= z₀, P(z₀)=0+C=C; P(z)=(z- z₀)H(z)+P(z₀)

z₀ – корень многочлена P(z₀)=(z- z₀)H(z), т.е. P(z) делится на (z- z₀) без остатка.

Следствие. Пусть z₀ – корень многочлена P(z) степени n>=1, тогда существует натуральное число l, 1<=l<=n, такое что P(z) можно записать в виде P(z)=(z- z₀)H(z), где degH=n-l, H(z₀)<>0.

Теорема (Основная теорема алгебры). Всякий многочлен P(z) степени n>=1 имеет хотя бы один корень.

Следствие основной теоремы алгебры. Всякий многочлен P(z) степени n>=1 имеет ровно n корней с учётом их кратности и для него справедливо разложение на линейные множители. P(z)=P_n(z-z₁)^m1…(z-z_s)^ms, где z₁…z_s различные корни многочлена (z_k<>z_l при k<>l), m₁,…,m_s кратности этих корней (1<=s<=n) и m₁+…+m_s=n, P_n – старший коэффициент при Zⁿ.

Разложение многочлена с вещественными коэффициентами на линейные и квадратичные множители.

Пусть P(z)=P0+P1z+…+PnZⁿ многочлен степени n>1 (т.е. Pn<>0) с вещественными коэффициентами P0, P1,…,Pn. Следовательно есть разложение на линейные множители. P(z)=P_n(z-z₁)^m1…(z-z_s)^ms, m₁+…+m_s=n, zk<>zl при k<>l. Коэффициенты вещественные, но среди корней могут быть комплексные. Отметим, что комплексные корни входят сопряжёнными парами, т.е. если z₀=+, <>0 – корень кратности l, то z₀(сопряж. число)= -i тоже корень кратности l.

Алгебра матриц.

Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаково длины (или n столбцов одинаковой длины).

Матрицы равны между собой, если равны все соответствующие элементы этих матриц.

Матрица, у которой число строк равно числу столбцов, называется квадратной.

Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.

матрица, содержащая один столбец или одну строку, называется вектором.

Матрица, полученная из данной заменой каждой её строки столбцом с тем же номером, называется матрицей транспонированной к данной.

Суммой двух матриц A и В называется матрица С такая, что cij=aij+bij.

Разностью двух матриц A и В называется матрица С такая, что cij=aij-bij.

Произведением матрицы А на число k называется матрица В такая, что bij=k*aij.

Матрица –A=(-1)*A называется противоположной матрице А.

Разность матриц можно определить как: А-В=А+(-В).

Операции сложения матриц и умножения матрицы на число обладают следующими свойствами:

• А+В=В+А;

• A+(B+C)=(A+B)+C;

• A+0=A;

• A-A=0;

• 1*A=A;

• *(A+B)=*A+*B;

• (+)*A=*A+*B

• *(A)=( )A.

Элементарные преобразования матриц:

• перестановка метами двух параллельных рядов матрицы;

• умножение всех элементов ряда матрицы на число, отличное от нуля;

• прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.

Две матрицы А и В называются эквивалентными, если одно из них получается из другой с помощью элементарных преобразований.

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

Произведением матрицы А(mn) на матрицу В(np) называется матрица C(mp) такая, что cik=ai1*b1k+ai2*b2k+…+ain*bnk, где i=1..m, k=1…p.

Матрицы А и В называются перестановочными, если АВ=ВА.

Св-ва умножения матриц:

• A(BC)=(AB)C;

• A(B+C)=AB+AC;

• (A+B)C=AC+BC;

• (AB)= (A)B.

Св-ва транспонирования:

• (A+B)^T=A ^T +B ^T;

• (AB) ^T=B ^T A ^T.

Пусть А – квадратная матрица n-го порядка.

При умножении квадратных матриц их определители перемножаются.

Квадратная матрица А называется невырожденной, если определитель не равен нулю, в противном случае матрица А называется вырожденной.

Матрицей, союзной к матрице А называется матрица

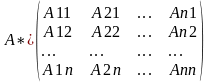, где Aij – алгебраическое дополнение элемента aij данной матрицы А.

Матрица А^-1 называется обратной матрице А, если выполняется условие А*А^-1=А^-1*А=Е.

Всякая невырожденная матрица имеет обратную.

Св-ва обратных матриц:

• если у матрицы А есть обратная, то определитель А<>0;

• если В= А^-1, то А=В^-1;

• если матрица А имеет обратную, только одну;

• если А и В имеют обратные, то произведения тоже имеют обратные матрицы, причём обратная к произведению есть произведение обратных в обратном порядке (АВ) ^–1=В^-1А^-1.

Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы.

Минор, порядок которого определяет ранг матрицы, называется базисным.

Крамер. AX+B.

Если определитель системы отличен от нуля, то система называется невырожденной.

X= А^-1B.

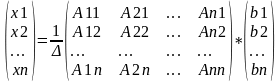
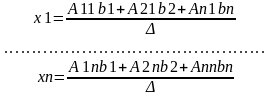
Но A11b1+A21b2+…+An1bn есть разложение определителя по элементам первого столбца.

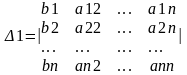
Определитель 1 получается из определителя  путём замены первого столбца коэффициентов столбцом из свободных. Итак, xi=i/ (формула Крамера).