
- •29. Экстраполяция и интерполяция динамических рядов.
- •30. Аналитические показатели рядов динамики. Методы изучения рядов динамики.
- •1. Основные понятия о рядах динамики
- •2. Виды рядов динамики
- •3. Основные показатели анализа динамических рядов
- •31. Индексный метод анализа, его значение. Виды индексов.
- •Индивидуальные индексы
- •Веса агрегатных индексов цен и физического объема продукции
- •Другие агрегатные индексы
- •32. Индексы переменного, постоянного состава, структурных сдвигов, их взаимосвязь.
- •33. Формы индексов, их взаимосвязь.
- •3. Средние индексы из индивидуальных
- •34. Виды и сущность взаимосвязей социально-экономических явлений.
- •6.1. Причинность, регрессия, корреляция
- •35. Построение уравнения парной регрессии.
- •1.2 Нормальная линейная модель парной регрессии
- •1.3 Альтернативный метод нахождения параметров уравнения парной регрессии
- •1.4 Классический метод наименьших квадратов (мнк) для модели парной регрессии
1.2 Нормальная линейная модель парной регрессии
Нормальная, или классическая, линейная модель парной регрессии (регрессии с одной переменной) строится исходя из следующих предположений:
факторный признак является неслучайной или детерминированной величиной, не зависящей от распределения случайной ошибки уравнения регрессии
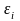 ;
;математическое ожидание случайной ошибки уравнения регрессии равно нулю во всех наблюдениях:
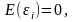 где
;
где
;
дисперсия случайной ошибки уравнения регрессии является постоянной для всех наблюдений:
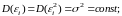
случайные ошибки уравнения регрессии не коррелированны между собой, т. е. ковариация случайных ошибок любых двух разных наблюдений равна нулю:
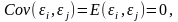 где
где
 .
.
Это предположение верно в том случае, если изучаемые данные не являются временными рядами;
основываясь на 3 и 4 предположениях, добавляется условие о том, что случайная ошибка уравнения регрессии является случайной величиной, подчиняющейся нормальному закону распределения с нулевым математическим ожиданием и дисперсией.
Исходя из указанных предпосылок, нормальную линейную модель парной регрессии можно записать в следующем виде:
 (1)
(1)
где – значения зависимой переменной ;
– значения независимой переменной;
– коэффициенты уравнения регрессии, подлежащие оценке;
- случайная ошибка уравнения регрессии.
Матричная форма нормальной линейной модели парной регрессии:
 (2)
(2)
где
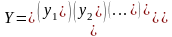 – вектор значений зависимой переменной
размерности nх1;
– вектор значений зависимой переменной
размерности nх1;
 – матрица значений независимой переменной
размерности nх2.
– матрица значений независимой переменной
размерности nх2.
Первый столбец является единичным, так как в уравнении регрессии параметр умножается на 1;
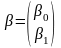 – вектор коэффициентов уравнения
регрессии размерности 2х1;
– вектор коэффициентов уравнения
регрессии размерности 2х1;
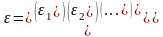 – вектор случайных ошибок уравнения
регрессии размерности nх1.
– вектор случайных ошибок уравнения
регрессии размерности nх1.
1.3 Альтернативный метод нахождения параметров уравнения парной регрессии
Традиционно параметры уравнения парной регрессии и оцениваются с помощью МНК, однако в случае парной регрессионной модели возможен и другой подход к оценке параметров регрессионной функции. Запишем уравнение парной регрессии в следующем виде:
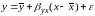 .
.
Здесь y – значение зависимой переменной;
x – значение независимой переменной;
– случайная ошибка;
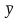 – среднее значение зависимой переменной,
вычисленное на основе выборочных данных.
Чаще всего это значение вычисляется по
формуле среднего арифметического:
– среднее значение зависимой переменной,
вычисленное на основе выборочных данных.
Чаще всего это значение вычисляется по
формуле среднего арифметического:
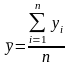 ,
,
где yi – значения зависимой переменной, ;
n – объем выборки;
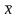 – среднее значение независимой
переменной, которое вычисляется
аналогично среднему значению зависимой
переменной;
– среднее значение независимой
переменной, которое вычисляется
аналогично среднему значению зависимой
переменной;
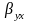 – выборочный коэффициент регрессии y
по x. Он характеризует на
сколько в среднем изменится результативный
показатель y при изменении
факторного показателя x
на единицу своего измерения.
– выборочный коэффициент регрессии y
по x. Он характеризует на
сколько в среднем изменится результативный
показатель y при изменении
факторного показателя x
на единицу своего измерения.
Оценка
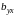 выборочного коэффициента регрессии y
по x вычисляется с помощью
следующей формулы:
выборочного коэффициента регрессии y
по x вычисляется с помощью
следующей формулы:
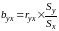 ,
,
где
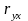 – выборочный парный коэффициент
корреляции, определяемый как
– выборочный парный коэффициент
корреляции, определяемый как
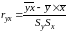 .
.
Выборочный парный коэффициент корреляции
показывает тесноту связи между изучаемыми
признаками. Он изменяется в пределах
[–1; +1]. Если
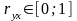 ,
то связь между признаками прямая. Если
,
то связь между признаками прямая. Если
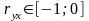 ,
то связь между признаками обратная.
Если
,
то связь между признаками обратная.
Если
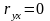 ,
то связь между признаками отсутствует.
Если
,
то связь между признаками отсутствует.
Если
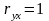 или
или
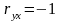 ,
то связь между изучаемыми признаками
является функциональной, т. е.
характеризуется полным соответствием
между x и y:
,
то связь между изучаемыми признаками
является функциональной, т. е.
характеризуется полным соответствием
между x и y:
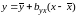 .
Примером функциональной зависимости
могут служить математические и
статистические формулы, например: S=a2.
При таком значении парного коэффициента
корреляции регрессионный анализ между
изучаемыми показателями не проводится.
Данная связь не подлежит численной
характеристике, так как на практике
массовым социально-экономическим
явлениям присущи иные виды связи (в
частности, корреляционная связь).
.
Примером функциональной зависимости
могут служить математические и
статистические формулы, например: S=a2.
При таком значении парного коэффициента
корреляции регрессионный анализ между
изучаемыми показателями не проводится.
Данная связь не подлежит численной
характеристике, так как на практике
массовым социально-экономическим
явлениям присущи иные виды связи (в
частности, корреляционная связь).
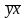 – среднее арифметическое значение
произведения результативного и факторного
признаков;
– среднее арифметическое значение
произведения результативного и факторного
признаков;
Sy – выборочное среднеквадратическое отклонение зависимой переменной y. Этот показатель вычисляется по формуле:
 ,
,
где
 – среднее значение квадратов значений
результативной переменной y:
– среднее значение квадратов значений
результативной переменной y:
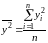 ,
,
 -
квадрат средних значений результативной
переменной y:
-
квадрат средних значений результативной
переменной y:
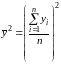 ,
,
Sx – выборочное среднеквадратическое отклонение независимой переменной x. Этот показатель вычисляется аналогично среднеквадратическому отклонению зависимого показателя y.
При
оценивании коэффициента
в модели регрессионной зависимости
результативного показателя y
от факторного показателя x
с помощью рассмотренного метода следует
помнить о том, что
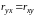 ,
но
,
но
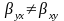 .
.
