4. Рассмотрим полученные углы.
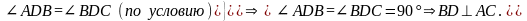
Теорема 2 (обратная). В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой его угла при вершине.
Дано: ∆АВС; АВ = ВС. BD – высота. Доказать: BD – биссектриса.
Доказательство:
Рассмотрим ABD = BCD.
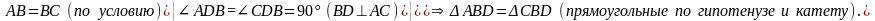
2. Из ∆ABD = ∆CBD AВD = СВD BD – биссектриса.
Теорема 3 (обратная). В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой его угла при вершине.
Дано: ∆АВС; АВ = ВС. BD – медиана. Доказать: BD – биссектриса.
Доказательство:
1. Рассмотрим ABD = BCD.
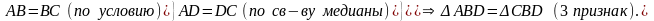
Билет 14
Классификация треугольников по величине углов:
1) Остроугольные – все углы меньше 90;
2) Прямоугольные – один угол равен 90, два других острые;
3) Тупоугольные – один угол больше 90 (тупой), два других острые.
В прямоугольном треугольнике стороны имеют свои названия. Стороны, образующие прямой угол, называются катетами, а третья сторона, лежащая против прямого угла, называется гипотенузой.
Способ доказательства от противного состоит в том, что сначала делается предположение, противоречащее тому, что утверждается в теореме. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходят к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании делается заключение, что предположение было неверным, а значит, верно утверждение теоремы.
Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство:
Допустим, что треугольники не равны тогда у них А ≠ А, В≠ В, C≠ C. Иначе они были бы равны по 1му признаку.
Пусть ∆A1B1С2 = ∆АBC, у которого вершина С2 лежит в той же полуплоск., что и в. С1.
Пусть D – середина отрезка С1 С2
∆A1С1С2 и ∆В1С1С2 – равнобедренные, с общим основанием С1С2. Поэтому их медианы A1D и B1D являются высотами. Значит прямые A1D и B1D перпендикулярны прямой С1С2.. Прямые A1D и B1D совпадают, т е точки A1, B1 , D не лежат на одной прямой. Но через точку D к прямой С1С2 можно провести только одну прямую, перпендикулярную данной.
Прямые наз-ся взаимно перпендикулярными, если при их пересечении образуются четыре прямых угла. Перпендикуляром к данной прямой наз-ся отрезок, который имеет одним из своих концов их точку пересечения. Этот конец отрезка наз-ся основанием перпендикуляра.
Билет 15
Биссектрисой треугольника называется отрезок, делящий внутренний угол треугольника пополам и проведенный из вершины до пересечения с противоположной стороной. .
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Высотой треугольника называется отрезок перпендикуляра, опущенный из вершины треугольника на противоположную сторону.
Точка пересечения биссектрис треугольника называется инцентром и является центром вписанной окружности.
Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром описанной окружности.
Точка пересечения медиан треугольника называется центром тяжести.
Точка пересечения высот треугольника называется ортоцентром треугольника. В отличие от других замечательных точек треугольника ортоцентр треугольника может находиться не только внутри треугольника, но и вне его.
2. Опр. Два угла, у которых одна сторона общая, а две другие являются дополнительными полупрямыми, называются смежными.
Теорема. Сумма смежных углов равна 180°.
Дано: АОС и ВОС – смежные.
Доказать:
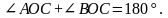
Доказательство:
1)
-
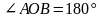развернутый.
2) Луч ОС лежит между сторонами АОВ. По аксиоме измерения углов:
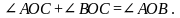
3)
Следовательно,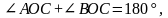
что и требовалось доказать.
Следствия:
1. Если два угла равны, то равны и смежные с ними углы.
Дано: АОС и ВОС – смежные;
PNK и KND – смежные;
АОС = PNK.
Доказать:
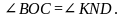
Доказательство:
1) АОС и ВОС – смежные
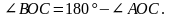
2) PNK и KND – смежные
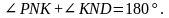
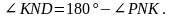
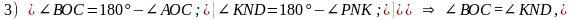
что и требовалось доказать.
2. Если угол не развернутый, то его градусная мера меньше 180°.
Дано: АОС – не развернутый.
Доказать:
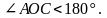
Доказательство:
1) Если АОС не развернутый, то, построив дополнительный к лучу ОА луч ОВ, получим ВОС – смежный с углом АОС.
2)
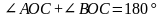(по свойству смежных углов)
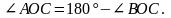
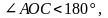что
и требовалось доказать.
Опр. Угол, равный 90°, называется прямым.
3. Угол, смежный с прямым углом, есть прямой угол.
Дано: АОС – прямой.
Доказать:
-
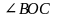прямой.
Доказательство:
1)
-
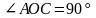по определению как прямой.
2) АОС и ВОС – смежные по свойству смежных углов.
3)
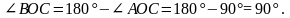
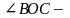прямой,
что и требовалось доказать.
Билет 16
Треугольники называются равными, если у них соответственные стороны и углы равны или можно совместить наложением.
В таком случае у них попарно равны все соответственные элементы:
АВ = А1В1; АС = А1С1; ВС = В1С1;
А = А1; В = В1; С = С1.
Обозначение равенства треугольников:
∆ АВС = ∆ А1В1С1.
Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Третий признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Дано: АВС и А1В1С1;
А = А1;
С = С1;
АС = А1С1.
Доказать:
АВС = А1В1С1.
Доказательство: