- Для двух бесконечных плоскостей.

Разность потенциалов между заряженными плоскостями определим, используя формулу (1.6):

(1.7)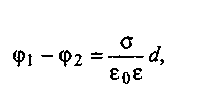

где d = x₂ – х₁ — расстояние между плоскостями обкладок.

Вопрос №4. Расчет поля равномерно заряженной сферической оболочки.

Оп­ределим напряженность и потенциал поля во внутренней и внешней областях равно­мерно заряженной сферической оболочки радиусом R. Заряд оболочки (σ - поверхностная плотность заряда).

Поле, создаваемое сферической оболочкой, является центрально-симметричным, поэтому для использования теоремы Гаусса в качестве замкнутой поверхности, сквозь которую будем находить поток смещения D, выберем сферу радиусом r (см. рис.6,а).

Рис.6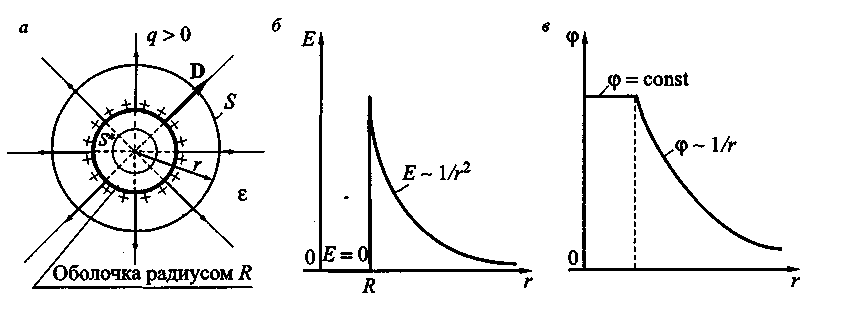

Рассмотрим поле вне оболочки, т.е. r>R. Во всех точках сферы S (рис. 6, а) смещение D одинаковое, причем вектор D направлен радиально от центра сферы при q > 0 и к центру при q < 0. Используя теорему (1.4), получаем поэтому смеще­ние D и напряженность E в этом случае рассчитывается по формулам

(1.8)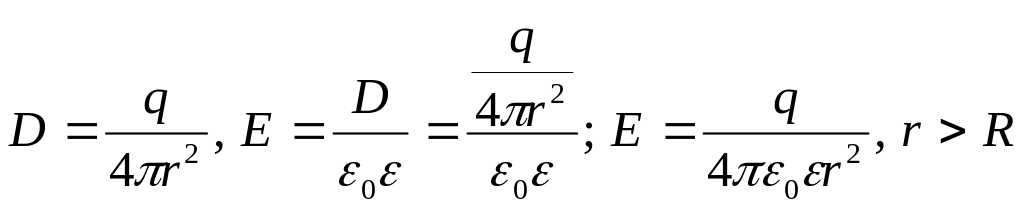

где ε — диэлектрическая проницаемость среды вне оболочки.

Поскольку для поля с центром симметрии напряженность Е = -dφ/dr, то потен­циал поля определим после разделения переменных и интегрирования в определен­ных пределах:

(1.9)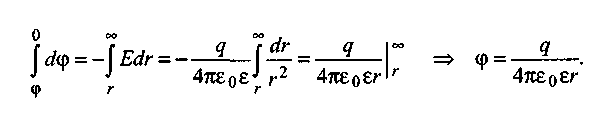

Здесь принято во внимание, что нулевой уровень для потенциала находится в беско­нечности, т.е. при r= ∞ потенциал φ = 0.

Для поля внутри оболочки (r < R) поверхность S* не охватывает заряды, поэтому D = 0, Е = 0, φ = const. Эта постоянная для потенциала φ должна быть такой, чтобы при г = R потенциал φ(r) был непрерывным.

Следовательно, постоянное значение потен­циала внутри оболочки и на самой оболочке равно . Найденные зависи­мости Е(r) и φ(r) изображены соответственно на рис. 6 (б, в).

Вопрос №5. Поле объемно заряженного шара

Пусть имеется диэлектрический шар радиусом R, заряженный с постоянной объемной плотностью .

Т.к. .

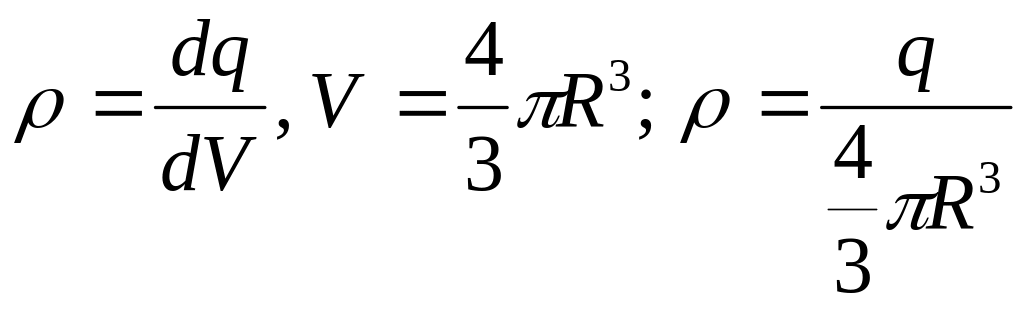В этом случае все соображения относительно симметрии поля и выбора поверх­ности для подсчета потока в теореме Гаусса будут такими же, как и для сферической оболочки. Для расчета поля внутри шара (r < R) используем поверхность S*:

(1.10)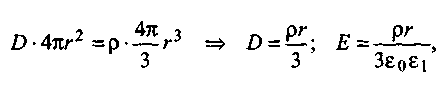

где ε₁— диэлектрическая проницаемость вещества шара.

Для расчета поля вне шара (г > R) используем поверхность S:

(1.10а )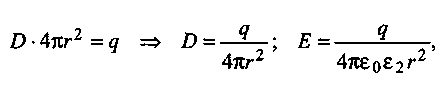

где ε₂ — диэлектрическая проницаемость среды вне шара(см рис. 7).

Рис. 7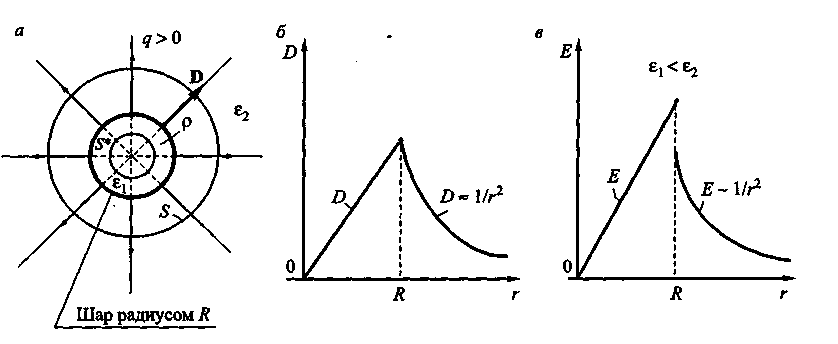

В этом случае потенциал φ также определяем интегрированием уравнения dφ =-Еdr. Графически зависимости D(r) и Е(r) изображены соответственно на рис. 7, а, б. Заметим, что на границе шара в случае, если е ε₁ ≠ ε₂, напряженность Е поля имеет раз­рыв (скачок) рис7,в , а смещение D изменяется непрерывно (рис 7,б).

Вопрос №6. Поле заряженных бесконечного цилиндра и прямой нити

Пусть поверхность бес­конечного цилиндра радиусом R заряжена с постоянной линейной плотностью λ = dq /dl = const. Электростатическое поле, создаваемое таким цилиндром, является ак­сиально-симметричным (рис. 8), т.е. имеет ось симметрии.

Рис. 8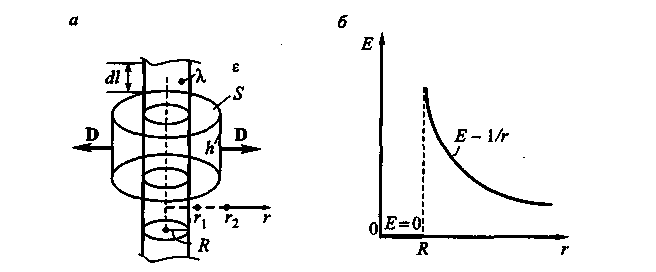

При расчете поля вне цилиндра (г > R) в качестве поверхности S, сквозь которую будем определять поток вектора D, выберем поверхность цилиндра радиусом г и вы­сотой h (рис. 8.). Из-за цилиндрической симметрии векторы D и Е поля перпенди­кулярны боковой поверхности S и численно равны между собой во всех точках этой поверхности. Поток вектора D сквозь верхнее и нижнее основания выбранного цилин­дра равен нулю, так как векторы D не пересекают эти основания (D_n = 0). Поэтому для поля вне цилиндра (г > R) по теореме Гаусса получим: - заряд, охватываемый поверхностью цилиндра радиусом г. Отсюда

(1.11)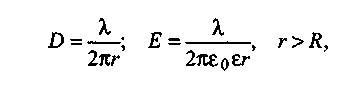

где е — диэлектрическая проницаемость среды, окружающей поверхностно заряжен­ный цилиндр радиусом R,

λ – линейная плотность.

Для поля внутри цилиндрической поверхности D = 0 и Е = 0, φ = const (заряд не охватывается поверхностью цилиндра радиусом г< R). Зависимость напряженности Е(г) изображена на рис. 8, б.

Разность потенциалов двух точек поля, находящихся от оси цилиндра на расстоя­ниях r₁и r₂, найдем, интегрируя соотношение dφ = -Еdr. Учитывая выражение (1.11) получаем

(1.11а)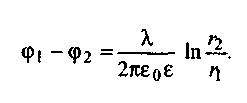

Отметим, что поле бесконечной прямой нити, заряженной с постоянной линей­ной плотностью, также рассчитывается по формулам (1.11) и (1.11а).

Литература:

1. И.И.Наркевич, З.И.Волмянский, С.И.Лобко. Физика. - Мн.:ООО «Новое знание»,2004.

2. А.Н.Вислович, Л.П.Гольман, С.И. Лобко и др. Сборник задач по физике для ВТУЗов. Часть 2, электричество и магнетизм. Мн.: издательство БГТУ,2002.

9