
- •Лекция № 4 Расчет полей заданных электрических зарядов
- •Вопрос №1. Электрическое смещение. Поток смещения.
- •Вопрос 2. Теорема Гаусса для вектора электрического смещения.
- •Вопрос №3. Расчет поля равномерно заряженных бесконечных плоскостей
- •- Для двух бесконечных плоскостей.
- •Вопрос №5. Поле объемно заряженного шара
- •Вопрос №6. Поле заряженных бесконечного цилиндра и прямой нити
Вопрос 2. Теорема Гаусса для вектора электрического смещения.
Рассчитаем поток вектора смещения D сквозь сферическую поверхность S радиусом r , которая совпадает с эквипотенциальной поверхностью поля, созданного точечным зарядом q (рис. 3, а).
Рис. 3, а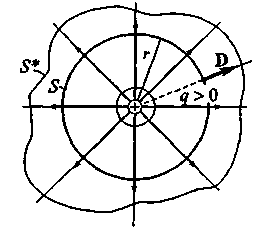
Согласно определению (1.3) с учетом выражения (1.2) имеем:
Рис. 3, б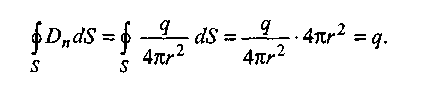
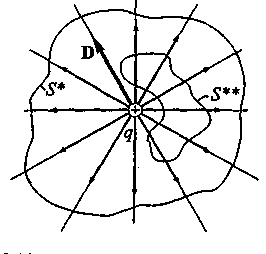
Поэтому для поля точечного заряда справедлива теорема, предложенная К.Гауссом: поток вектора электрического смещения D поля точечного заряда q сквозь любую замкнутую поверхность S равен заряду q, если эта поверхность охватывает заряд, и равен нулю, если поверхность не охватывает заряд.
Ф = q – если поверхность охватывает заряд,Ф = 0 – если поверхность не охватывает заряд.
С учетом принципа суперпозиции эту теорему можно распространить на произвольную систему электрических зарядов, создающих поле. В общем случае теорема Гаусса для электрического поля утверждает: поток вектора электрического смещения D сквозь любую замкнутую поверхность равен алгебраической сумме свободных зарядов, охватываемых этой поверхностью, т.е.:
(1.4)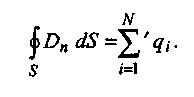
Здесь N— число зарядов, причем суммирование проводится только по тем зарядам, которые попали внутрь замкнутой поверхности (на это указывает штрих у знака суммы).
Если заряд распределен каким-либо образом, то суммарный заряд определяется путем интегрирования.
Теорема Гаусса позволяет рассчитывать характеристики симметричных электрических полей заряженных тел простейшей геометрической формы, причем вычисления проводить намного проще, чем на основании принципа суперпозиции. Это видно из следующих примеров. Задача 3.
Вопрос №3. Расчет поля равномерно заряженных бесконечных плоскостей
Рассмотрим поле, создаваемое одной бесконечной плоскостью, которая равномерно заряжена с постоянной поверхностной плотностью σ. Из соображений симметрии следует, что вектор D направлен перпендикулярно плоскости так, как это показано на рис. 4, а (σ > 0), а его числовое значение будет одинаковым во всех точках пространства, расположенных на одинаковых расстояниях слева и справа от плоскости. Поэтому в качестве замкнутой выберем цилиндрическую поверхность, основания которой параллельны плоскости, а ось перпендикулярна ей.
Тогда в точках
левого и правого оснований проекция
Dn=D,
а в точках боковой поверхности Dn
= 0, так как вектор D параллелен образующим
боковой поверхности. Охватываемый
цилиндром заряд
![]() поэтому уравнение (1.4) примет вид:
поэтому уравнение (1.4) примет вид:
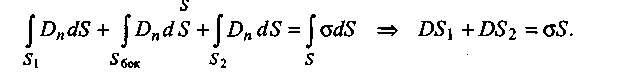
Поскольку S1 = S2 = S, окончательно получим:
D =σ / 2 – для одной плоскости.
Рис. 4, а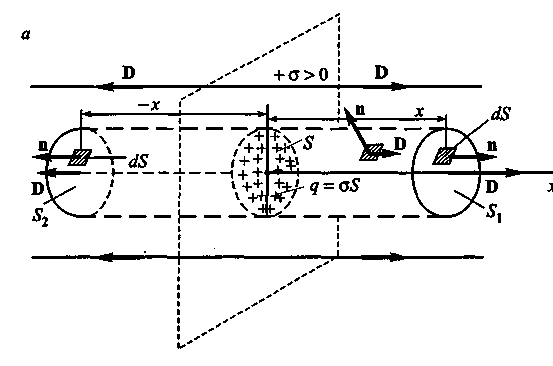
![]() отсюда следует
отсюда следует
![]() в
результате чего получим:
в
результате чего получим:
(1.5)![]()
Разность потенциалов
двух точек пространства, находящихся
на расстоянии х1
и x2
от заряженной плоскости (рис. 4, б),
рассчитаем путем интегрирования,
используя формулу для взаимосвязи
![]() =
- grad
φ (Е = Δ φ ). Для этого случая получим:
=
- grad
φ (Е = Δ φ ). Для этого случая получим:
(1.6)
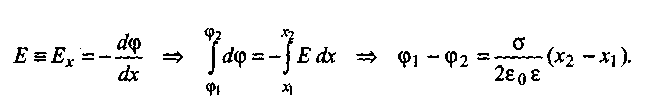
Рис. 4, б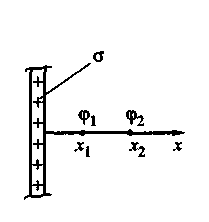
Поле двух параллельных бесконечных плоскостей, заряженных равномерно с поверхностными плотностями +σ и - σ, т.е. плоского конденсатора( в случае реального плоского конденсатора поле создается обкладками конечного размера, однако, если расстояние d между ними намного меньше линейных размеров обкладок, их можно считать бесконечными), рассчитаем с помощью принципа суперпозиции, складывая напряженность полей, создаваемых каждой плоскостью в отдельности (см.рис. 5).
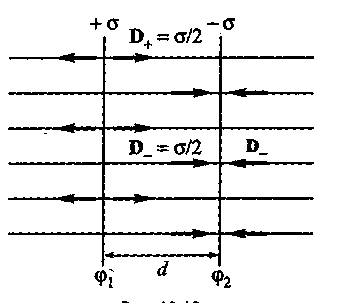
![]()
Из рис. 5. видно, что поля обкладок конденсатора слева и справа от их плоскостей взаимно компенсируют друг друга (D = 0, Е = 0), а между ними смещение D и напряженность Е увеличиваются в 2 раза, поэтому (D+ = D_ = σ / 2):
