
КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
Комплексными
числами
называются числа вида
![]() ,
где
,
где
![]() – действительные числа,
– действительные числа,
![]() – действительная часть,
– действительная часть,
![]() – мнимая часть комплексного числа.
– мнимая часть комплексного числа.
По определению,
два комплексных числа:
![]() и
и
![]() – равны тогда и только тогда, когда
– равны тогда и только тогда, когда
![]() и
и
![]() .
.
Комплексное
число
![]() называется сопряженным комплексному
числу
называется сопряженным комплексному
числу
![]() ,
если
,
если
![]() .
Другими словами, если
,
то
.
Другими словами, если
,
то
![]() .
.
Всякому
комплексному числу
![]() можно поставить в соответствие
единственную точку плоскости
можно поставить в соответствие
единственную точку плоскости
![]() и обратно, всякую точку
плоскости
и обратно, всякую точку
плоскости
![]() можно рассматривать как геометрический
образ единственного комплексного числа
.
можно рассматривать как геометрический
образ единственного комплексного числа
.
М
0 х Рисунок 1
|
Для сокращения
вместо “точка, соответствующая
комплексному числу
”,
говорят просто “точка
”.
При этом множество всех действительных
чисел изображается точками оси абсцисс,
которая поэтому называется действительной
осью, множество чисто мнимых чисел
|
нат, изображает действительное число нуль. Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью.
В некоторых
случаях удобно считать геометрическим
изображением числа
радиус-вектор точки
![]() –
–
![]() .
.
0 z3 5 x -2 z2
-5 z1 Рисунок 2 |
Пример 1.
Построить точки
В дальнейшем, наряду с представлением комплексных чисел в декартовых координатах, полезно иметь их представление в обобщенных полярных координатах. Рассмотрим
число
,
которому на плоскости соответствует
точка
.
Ее координаты в полярной системе
координат
|
y M(x; y) ρ
φ 0 x Рисунок 3 |
Тогда
Полярный
радиус
|
Полярный угол
![]() называется аргументом
комплексного
числа и обозначается
называется аргументом
комплексного
числа и обозначается
![]() .
Тогда
.
Тогда
![]() .
.
Эта форма называется тригонометрической формой комплексного числа.
Модуль комплексного
числа определяется однозначно:
![]() .
.
Аргумент
комплексного числа определяется с
точностью до слагаемого, кратного
![]() .
Главным значением аргумента называется
значение, заключенное в интервале
.
Главным значением аргумента называется
значение, заключенное в интервале
![]() .
Обозначается оно
.
Обозначается оно
![]() .
Таким образом,
.
Таким образом,
![]() .
.
Очевидно,
![]() .
.
Главное значение аргумента определяется однозначно.
Так как
![]() ,
,

Тригонометрическая форма комплексного числа будет иметь вид
![]() .
.
Задача 1.
Написать в тригонометрической форме
комплексное число
![]() .
.
z 1
-1 0 x
Рисунок 4 |
Решение.
|
Пусть
![]() .
Используя формулу Эйлера
.
Используя формулу Эйлера
![]() ,
получаем так называемую показательную
форму записи
комплексного числа:
,
получаем так называемую показательную
форму записи
комплексного числа:
![]() .
.
Задача 2.
Представить в показательной форме
комплексное число
![]() .
.
-1 0 x
z -1 Рисунок 5 |
Решение
|
Пример 2.
Вычислить
![]() .
.
Решение.
По формуле Эйлера
![]() .
.
АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМ
Сложение и
умножение
комплексных чисел производится по
правилам сложения и умножения
алгебраических многочленов с учетом
![]() .
При записи результата следует отделить
действительную часть от мнимой, т. е.
собрать отдельно члены, содержащие
множитель
.
При записи результата следует отделить
действительную часть от мнимой, т. е.
собрать отдельно члены, содержащие
множитель
![]() ,
и члены, не содержащие множитель
,
и члены, не содержащие множитель
![]() :
:
![]()
![]()
![]()
В частности,
![]() .
Операции сложения и вычитания сводятся
к сложению и вычитанию векторов,
изображающих эти числа. Отсюда расстояние
между точками
.
Операции сложения и вычитания сводятся
к сложению и вычитанию векторов,
изображающих эти числа. Отсюда расстояние
между точками
![]() .
.
y
z1 z1+z2
z2 z1-z2
Рисунок 4
|
Пример 2.
Деление на комплексное число, отличное от нуля, определяется как действие, обратное умножению. Для представления частного в виде
следует провести простые преобразования, показанные на следующем пример Задача
3.
|
Можно доказать
методом полной математической индукции,
что для любого целого
![]() (формула Муавра). Формула справедлива
и для целых отрицательных
(формула Муавра). Формула справедлива
и для целых отрицательных
![]() .
.
Пример 3.
Вычислить
![]() .
.
0 x
-1 z Рисунок 5 |
Решение
По формуле Муавра при n=5 имеем |
 ,
,

 .
.
Для модуля и аргумента произведения и частного справедливы следующие утверждения:
Корнем
![]() -й
степени из комплексного числа называется
такое число
-й
степени из комплексного числа называется
такое число
![]() ,
для которого
,
для которого
![]() .
.
Используя формулу Муавра, получим
![]()
Для других
значений
![]() аргументы будут отличаться от полученных
на число кратное
,
и, следовательно, получатся значения
корня, совпадающие с рассмотренными.
Итак, корень
-й
степени из комплексного числа имеет
различных значений.
аргументы будут отличаться от полученных
на число кратное
,
и, следовательно, получатся значения
корня, совпадающие с рассмотренными.
Итак, корень
-й
степени из комплексного числа имеет
различных значений.
Задача 4.
Найти все значения
![]() и построить их.
и построить их.
Рисунок 6 |
Решение.
|
 ,
,
 ,
,
 .
.
Типовой расчет «Комплексные числа» Задача 1
Представить комплексное число в тригонометрической форме:
1. |
|
2. |
|
3. |
|
4. |
|
5. |
|
6. |
|
7. |
|
8. |
|
9. |
|
10. |
|
11. |
|
12. |
|
13. |
|
14. |
|
15. |
|
16. |
|
17. |
|
18. |
|
19. |
|
20. |
|
21. |
|
22. |
|
23. |
|
24. |
|
25. |
|
26. |
|
27. |
|
28. |
|
29. |
|
30. |
|
Задача 2
Представить число в показательной форме:
1. |
|
2. |
; |
3. |
|
4. |
|
5. |
|
6. |
|
7. |
; |
8. |
|
9. |
|
10. |
|
11. |
|
12. |
|
13. |
; |
14. |
; |
15. |
|
16. |
; |
17. |
; |
18. |
|
19. |
|
20. |
|
21. |
; |
22. |
; |
23. |
; |
24. |
; |
25. |
; |
26. |
; |
27. |
; |
28. |
|
29. |
; |
30. |
|
Задача 3
Выполнить указанные действия:
1. |
|
2. |
|
3. |
|
4. |
|
5. |
|
6. |
|
7. |
|
8. |
|
9. |
|
10. |
|
11. |
|
12. |
|
13. |
|
14. |
|
15. |
|
16. |
|
17. |
|
18. |
|
19. |
|
20. |
|
21. |
|
22. |
|
23. |
|
24. |
|
25. |
|
26. |
|
27. |
|
28. |
|
29. |
|
30. |
|
Задача 4
Вычислить корень:
1. |
|
2. |
|
3. |
|
|
4. |
|
5. |
|
6. |
|
|
7. |
|
8. |
|
9. |
|
|
10. |
|
11. |
|
|||
Решить уравнение: |
||||||
12. |
|
13. |
|
14. |
|
|
15. |
|
16. |
|
17. |
|
|
18. |
|
19. |
|
20. |
|
|
21. |
|
22. |
|
23. |
|
|
24. |
|
25. |
|
26. |
|
|
27. |
|
28. |
|
29. |
|
|
30. |
|
|||||

 y
y y
y
 y
y .
. y
y
 .
. y
y ,
, y
y
 ,
, ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;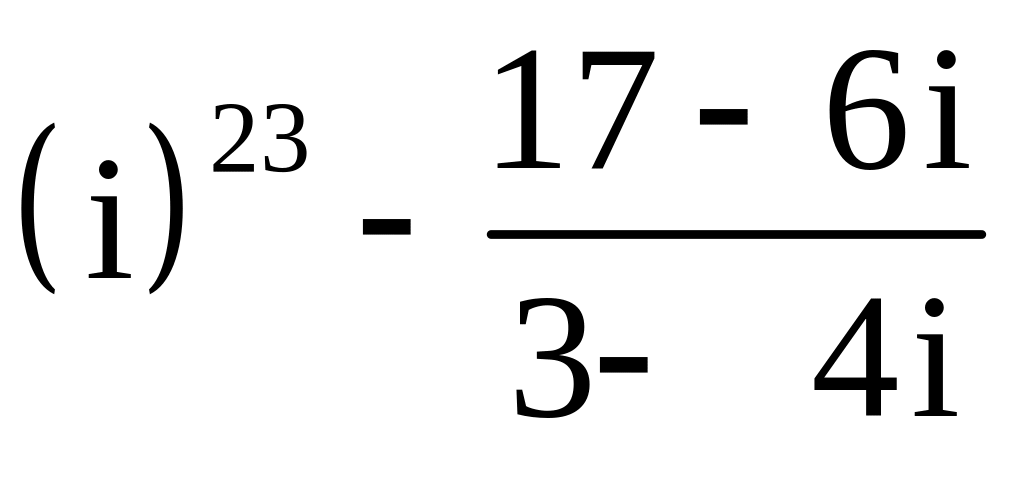 ;
; ;
;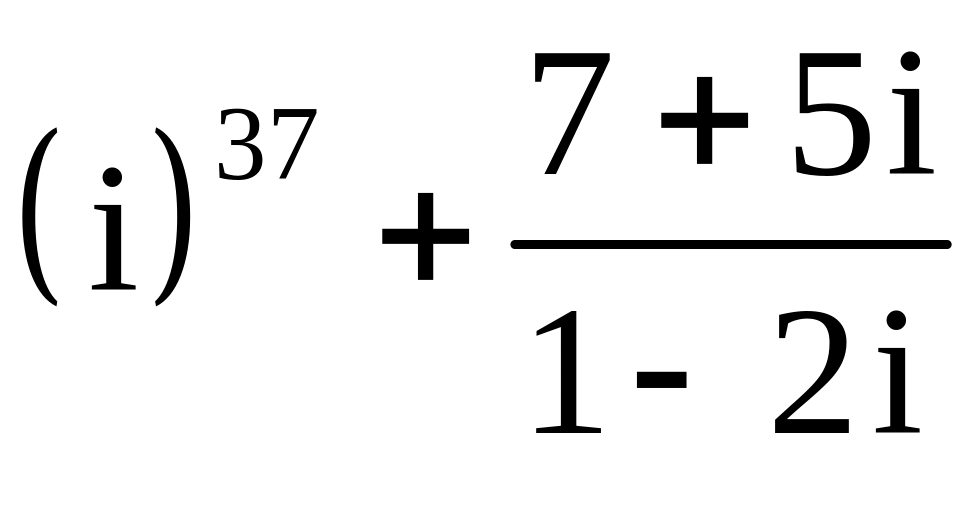 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
.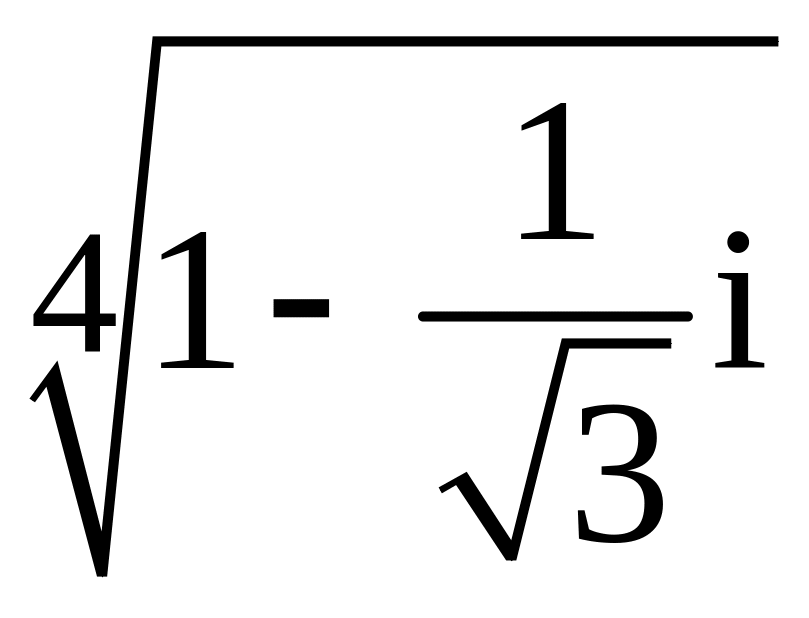 ;
;