4. Метод Жордана-Гауса

Метод Жордана-Гауса реалізується наступним алгоритмом.

Алгоритм: Система

Представимо її у вигляді таблиці

(1)

В таблиці вибираємо будь-який ключовий елемент, відмінний від нуля і не стоячий в стовпчику вільних членів( якщо можливо, то простіше в якості ключового елементу брати 1). Проводимо крок Жорданових виключень з вибраним ключовим елементом. В результаті одержуємо таблицю, в якій зліва буде деяке х , а зверху над стовпчиком-нуль. Викреслюємо цей стовпчик(тобто минулий стовпчик з ключовим елементом).

Повторюємо дію 2 до тих пір, поки не будуть переведені всі х вліво таблиці, тобто поки не прийдемо до таблиці ,

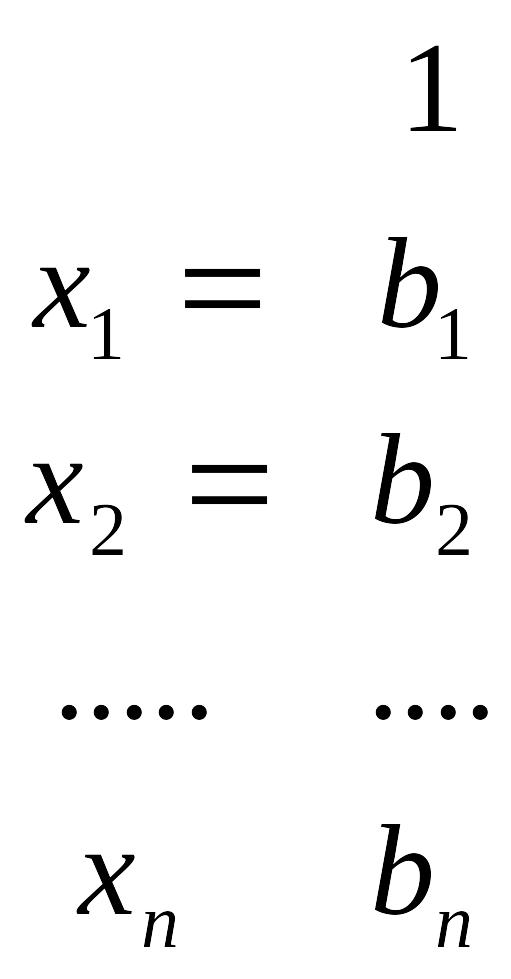із якої і одержуємо розв`язок х , х , ..., .

ПРИКЛАД1: Знайти розв`язок системи рівнянь методом Жордано-Гауса.

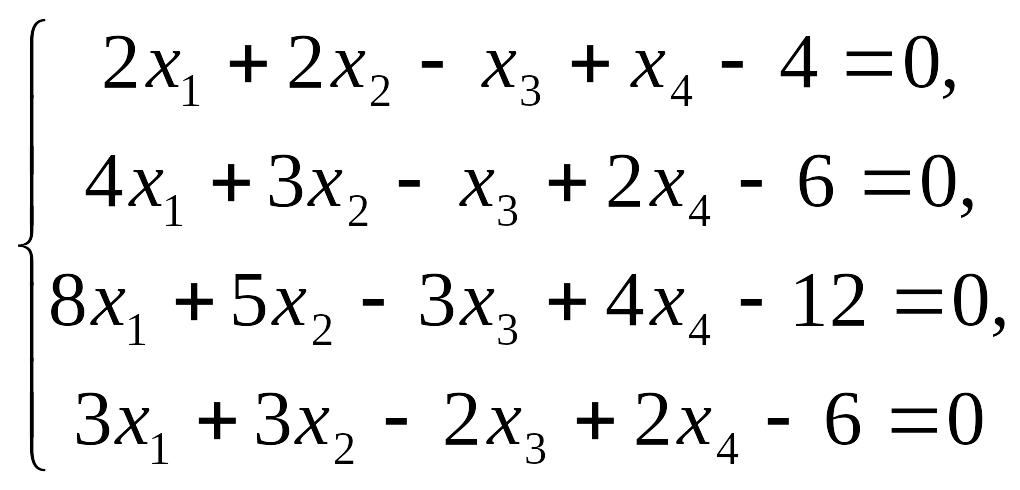
Розв`язання: Запишемо дану систему у вигляді .

Зробимо один крок Жорданових виключень з ключовим елементом а =1 і викреслюємо потім четвертий стовбець, що стоїть під нулем, одержимо таблицю .

Наступний крок зробимо з ключовим елементом, що стоїть у другому рядочку і третьому стовпчику. Після викреслювання третього стовпчика одержимо

.

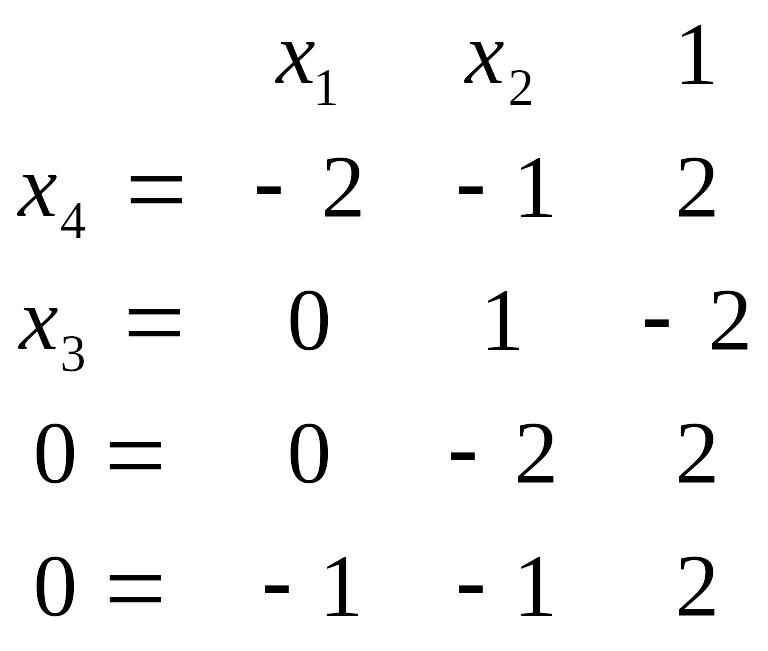Третій крок перетворень з ключовим елементом, що стоїть у четвертому рядочку і другому стовпчику, приводить до таблиці

, або .

Після четвертого кроку знайдемо остаточно .

Звідси х , х х х .

Зауваження: 1. Якщо визначник системи рівний нулю, (тобто система або несумісна, або має нескінчене число розв`язків, що виявляється в процесі розв`язання), то в результаті обчислення одержиться ситуація, коли деякі х залишаться зверху таблиці, а нулі - зліва і неможливо буде вибрати ключовий елемент, так як всі елементи в нуль стрічках нулі. Якщо при цьому і вільні члени цих стрічок (в стовпчику під 1) нулі, то система має нескінчене число розв`язків. В інакшому випадку система не має розв`язку.

Зауваження: 2. Описаний метод можна застосовувати і для розв`язування прямокутних систем (число рівнянь не рівне числу невідомих).

ПРИКЛАД 2: Розв`язати систему рівнянь методом Жордано-Гауса.

Розв`язання: Запишемо дану систему у вигляді

.

Виконаємо крок Жорданових виключень з ключовим елементом, що стоїть у першому рядочку і першому стовпчику, одержимо

.

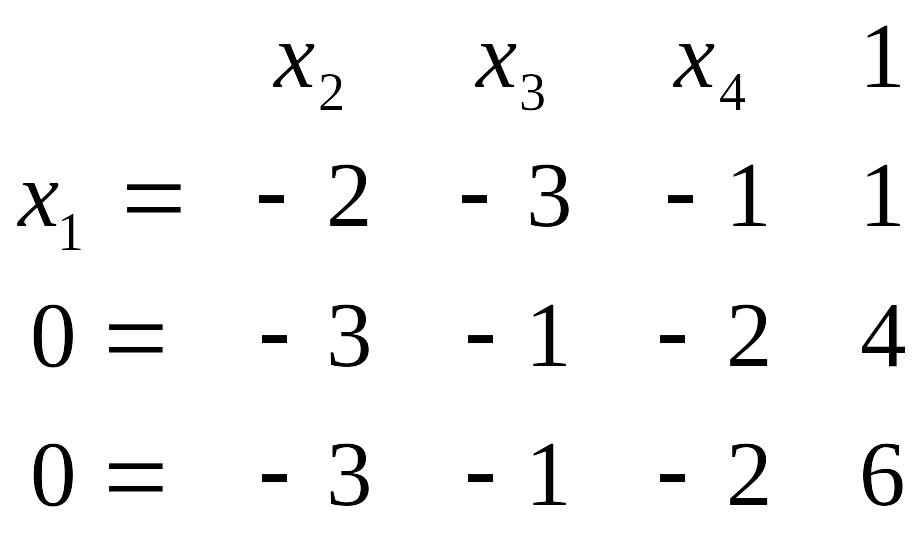Виконаємо крок Жорданових виключень з ключовим елементом, що стоїть у другому стовпчику і третьому рядочку, одержимо

.

Подальші обчислення неможливі, так як в залишеній нуль стрічці елементи під х і х нулі. Вільний член цієї стрічки не нуль, тому система несумісна: 0 -2.

6. Метод Гауса.Цей метод відрізняється від методу Жордано-Гауса лише тим, що після кожного кроку Жорданових виключень викреслюємо не тільки стовпчик з ключовим елементом, але і рядочок із ключовим елементом, але при цьому виписуємо окремо вираз для відповідного х .

Запишемо систему n рівнянь з невідомими у вигляді таблиці

Виберемо в якості ключового елемента будь-який елемент таблиці, відмінний від нуля і не стоїть в стовпчику вільних членів. Проведемо крок Жорданових виключень з ключовим елементом, після чого викреслюємо із таблиці стовпчик з ключовим елементом і виписуємо рядочок, що відповідає невідомому х . Повторяємо дію 2 до тих пір, поки не прийдемо до таблиці вигляду , тобто х .

Підставляємо послідовно з кінця до початку знайдені значення для х до тих пір, поки не одержимо значення всіх невідомих.

ПРИКЛАД: Розв`язати систему лінійних рівнянь методом Гауса

Розв`язання: Перепишемо систему у вигляді таблиці

Вибираємо за ключовий елемент одиницю, що стоїть в першому рядочку і четвертому стовпчику. Проведемо крок Жорданових виключень. Викреслюємо четвертий стовпчик і виписуємо окремо першу стрічку, що представляє вираз для х . Будемо мати

,

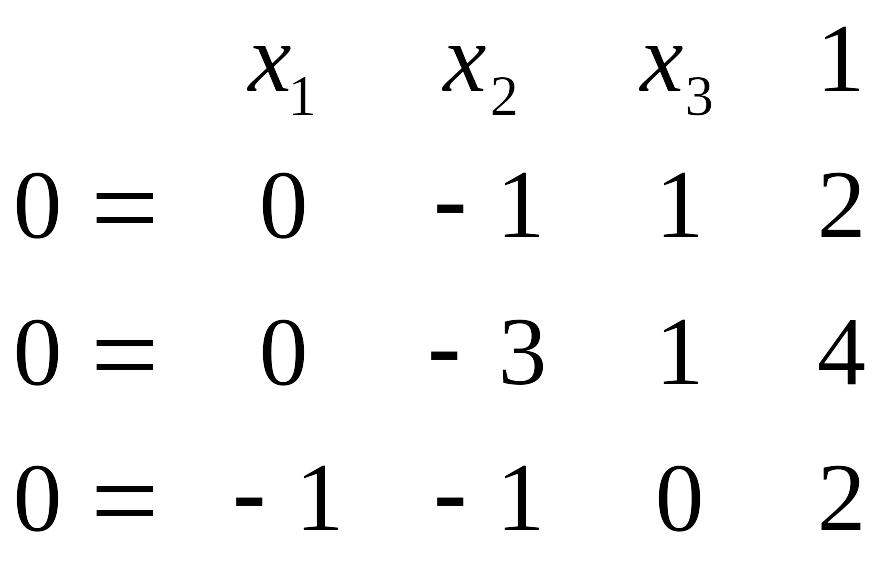і

Вибираємо ключовий елемент одиницю, що стоїть в першому рядочку і третьому стовпчику. Проводимо крок Жорданових виключень і викреслюємо перший рядочок і третій стовпчик. Одержимо

, .

Проводимо крок Жорданових виключень з ключовим елементом -1, що стоїть у другому стовпчику і другому рядочку. Одержимо

, .

Знаходимо із останньої таблиці х =1. Підставимо його у вираз для х , одержимо х =-1+2=1, далі х =1-2=-1 і х =-2-2-1+4=-1.

Зауваження: 1. Якщо визначник системи рівний нулю, (тобто система або несумісна, або має нескінчене число розв`язків, що виявляється в процесі розв`язання), то в результаті обчислення одержиться ситуація, коли деякі х залишаться зверху таблиці, а нулі - зліва і неможливо буде вибрати ключовий елемент, так як всі елементи в нуль стрічках нулі. Якщо при цьому і вільні члени цих стрічок (в стовпчику під 1) нулі, то система має нескінчене число розв`язків. В інакшому випадку система не має розв`язку.

Зауваження: 2. Описаний метод можна застосовувати і для розв`язування прямокутних систем (число рівнянь не рівне числу невідомих).

Жорданові виключення можуть бути застосовані і для відшукання оберненої матриці. Нехай дана квадратна матриця

А= ,

визначник якої не рівний нулю (А- не вироджена матриця). Представимо її у вигляді (1), позначивши через х (j=1, ...,n) стовпчики матриці, а через y (і=1,...,n) рядочки:

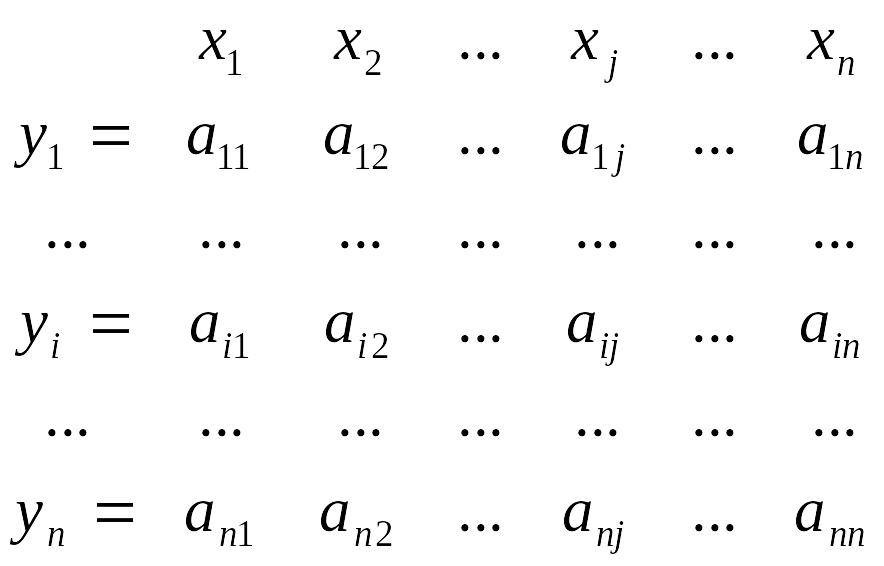(1)

Проведемо над таблицею послідовно n кроків Жорданових виключень, перекинувши при цьому всі х вліво, а у вверх таблиці. Потім, якщо треба, переставимо рядки і стовпчики так, щоб х і у розміщувались в порядку зростання їх номерів. Кінцева таблиця має вигляд

і матрицею цієї таблиці являється А , обернена матриця А.

ПРИКЛАД: Дана невироджена матриця А= .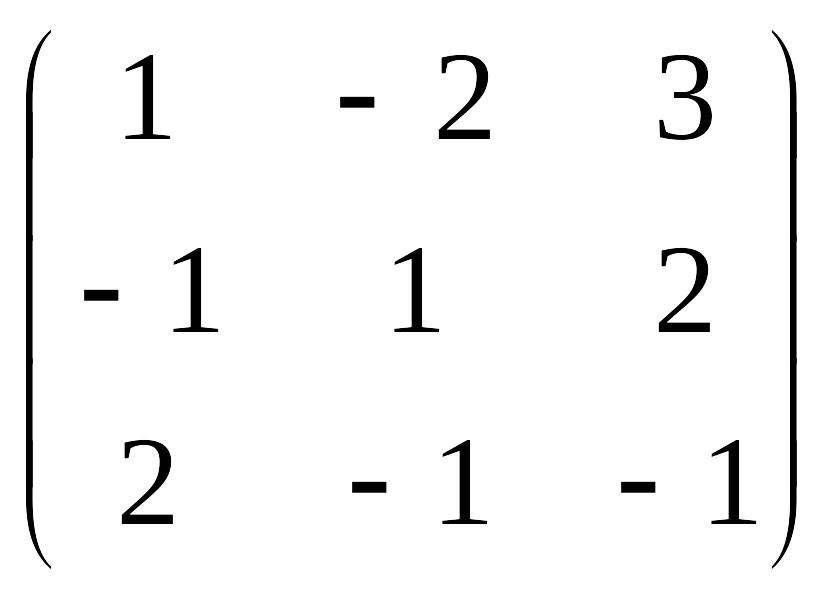

Знайти матрицю А .

Розв`язання: Представимо матрицю у вигляді таблиці

Зробивши один крок Жорданових виключень з ключовим елементом, що знаходиться в першому рядку і першому стовпчику, одержимо таблицю

(:1)

Тепер зробимо ще один крок Жорданових виключень з кореневим елементом, що стоїть у другому стовпчику і у другому рядочку. Одержимо

(:-1)

і після ділення прийдемо до таблиці

.

Накінець, помінявши ролями х і у , одержимо таблицю

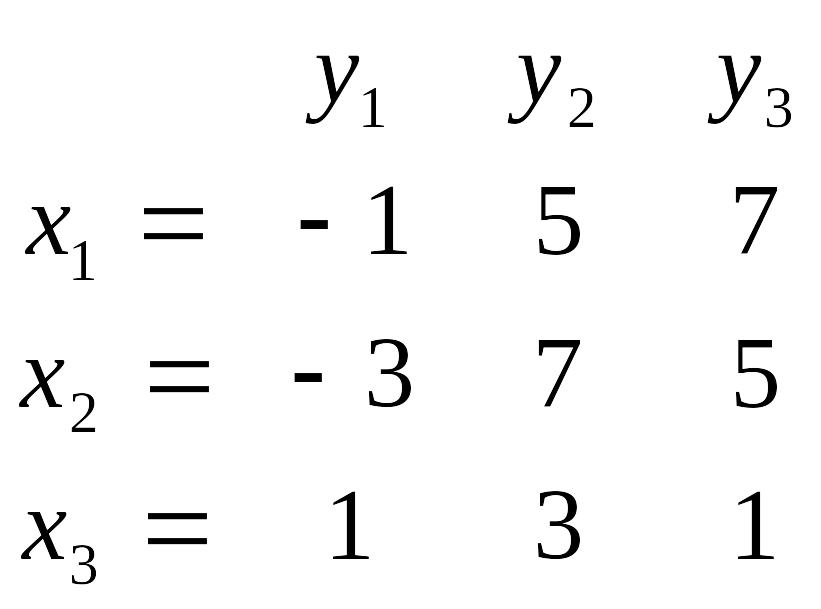(:8).

В кінцевому рахунку

На цьому обчислення закінчується і оберненою буде матриця, записана в останній таблиці. Зазвичай в таблиці, отриманій після виконання всіх кроків Жорданових виключень, приходиться ще переставляти деякі рядки і стовпчики, якщо серед ключових елементів не всі були діагональними.

Зауваження: Якщо матриця А вироджена, тобто =0, то це виявиться в процесі розв`язку. Певні y не вдається перекинути вверх таблиці (або х вліво таблиці). Така ситуація виникає, якщо на перетині рядка y і всіх стовпчиків, зверху яких х , стануть нулі. Максимальне число y , перекинутих вверх таблиці (або х - вліво таблиці), буде рівне рангу матриці А.

МЕТОД ОБЕРНЕНОЇ МАТРИЦІ

Жорданові виключення дозволяють відшукати розв`язок системи n рівнянь з n невідомими третім способом – методом оберненої матриці. Для цього запишемо систему у вигляді .

Проробивши послідовно n кроків Жорданових виключень, після можливих перестановок стрічок і стовпчиків, одержимо

, або .

 

Звідси

Лекція 4: Наближені методи розв'язування систем лінійних алгебраїчних рівнянь