35. Диференціальні рівняння 1 порядку з відокремленими змінними

Якщо в диференціальному рівнянні першого порядку

(12.1)

праву частину можна подати у вигляді

то (за умови, що ) це рівняння можна записати так:

(12.2)

Розглядаючи цю рівність як рівність двох диференціалів та інтегруючи зліва за , а справа за , отримаємо

(12.3)

Це співвідношення є загальним інтегралом рівняння (12.1).

Диференціальне рівняння першого порядку типу (12.2), в якому при диференціалах та стоять відповідно функції, залежні тільки від чи тільки від , називається диференціальним рівнянням з відокремленими змінними.

Диференціальне рівняння вигляду

(12.4)

називається рівнянням з відокремлюваними змінними.

Справді, якщо , то змінні відокремлюються діленням обох частин рівняння (12.4) на . Маємо

і, отже, загальний інтеграл рівняння, за аналогією з (12.2), має вигляд

.

\Приклад 1 . Нехай осіб зацікавлені в одержані інформації про новини технології у деякій галузі знань. Нехай в момент часу інформація відома особам. Для прискорення поширення інформації в момент часу було дано оголошення (наприклад, по радіо). Далі інформація поширюється при спілкуванні людей між собою. Можна вважати, що після оголошення швидкість зміни кількості тих, хто знає про технологічні новини, пропорційна як числу тих, хто знає, так і кількості

тих, хто не знає. Припускаючи, що в момент часу про новину дізналося чоловік, приходимо до диференціального рівняння

(12.5)

з початковою умовою ( - коефіцієнт пропорціональності).

Це диференціальне рівняння першого порядку з відокремлюваними змінними. Подамо його у вигляді

.

Загальний інтеграл рівняння

(12.6)

Знайдемо інтеграл у лівій частині рівності (12.6):

(Зауважимо, що ). Загальний інтеграл (12.6) має форму

.

Звідси знаходимо загальний розв’язок :

(12.7)

Для отримання розв’язку задачі Коші покладемо в рівності (12.7) та визначимо довільну сталу (у даному

прикладі зручно шукати не , а ) . Маємо , звідки

(12.8)

Підставимо вираз (12.8) у загальний розв’язок (12.7) і спростимо результат. Отримаємо шуканий частинний розв’язок:

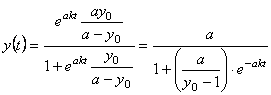. (12.9)

Його графіком є так звана логістична крива (рис.12.1).

36. Лінійне програмування.Приклади задач лінійного програмцвання

Під метою будемо розуміти той кінцевий результат, який необхідно отримати шляхом вибору та реалізації тих чи інших управляючих впливів на досліджувану систему. У виробничо-комерційній сфері мета полягає в тому, щоб або максимізувати прибуток, або мінімізувати витрати. Коли мета визначена, оптимальним вважається такий спосіб дій, який найбільшою мірою сприяє досягненню цієї мети. Однак «якість» реалізації процедури вибору залежить від того, наскільки повно відомі допустимі альтернативи керуючих впливів. Потрібно виявити повне безліч так званих керованих змінних. Важливим моментом при прийнятті управлінських рішень є ідентифікація некерованих змінних, тобто суб'єкта управління. Для побудови математичної моделі необхідно мати суворе уявлення про мету функціонування досліджуваної системи і мати інформацію про обмеження, які визначають область допустимих значень керованих змінних. Як мета, так і обмеження мають бути представлені у вигляді функцій від керованих змінних. Аналіз моделі повинен привести до визначення найкращого керуючого впливу на об'єкт управління при виконанні всіх установлених обмежень. При спрощеному описі реальних систем, на основі якого буде будуватися та чи інша модель, перш за все слід ідентифікувати домінуючі змінні, параметри і обмеження. Модель, будучи подальшим спрощенням образу системи-оригіналу, являє собою найбільш істотні для опису системи співвідношення у вигляді цільової функції і сукупності обмежень. Найбільш важливим типом моделей є математичні моделі. В основі їх побудови лежить припущення про те, що всі релевантні змінні, параметри та обмеження, а також цільова фукцией кількісно вимірні. Тому якщо являє собою керованих змінних і умови функціонування досліджуваної системи хаарктерізуются обмеженнями, то математична модель може бути записана в наступному вигляді: Знайти оптимум (Цільова функція) при обмеженнях 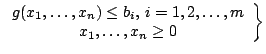Обмеження - Умови неотрицательности. Знаходження оптимуму здійснюється для визначення найкращого значення цільової функції (максимуму прибутку або мінімуму витрат, наприклад). Отримане за допомогою деякої моделі конкретне оптимальне рішення є найкращим тільки в рамках використання тільки цієї моделі. Не слід вважати, що знайдений оптимум - це дійсно найкраще рішення аналізованої завдання. Воно є найкращим з усіх можливих тоді, коли вибраний критерій оптимізації можна вважати цілком адекватним кінцевим цілям організації, в якій виникла досліджувана проблемна ситуація.