Лабораторная работа №3 Спектральное представление периодических процессов в электрических цепях

1. Общие сведения

Во многих случаях в установившемся режиме кривые периодических э.д.с., напряжений и токов в электрических цепях могут отличаться от синусоидальных. При этом непосредственное применение символического метода для расчета цепей переменного тока становится невозможным. Для линейных электрических цепей задача расчета может быть решена на основе метода суперпозиции с использованием спектрального разложения несинусоидальных напряжений и токов в ряд Фурье. В общем случае ряд Фурье содержит постоянную составляющую, первую гармонику, частота которой совпадает с частотой ω₁=2π/T периодического с периодом T тока или напряжения, и набор высших гармоник с частотами ω_n=nω₁, кратными основной частоте ω₁. Для большинства периодических функций ряд Фурье содержит бесконечное число членов. На практике ограничиваются конечным числом членов ряда. При этом исходная периодическая функция будет представлена с помощью ряда Фурье с некоторой погрешностью.

Пусть имеется периодическая с периодом Т э.д.с. е(t)=e(t±nT), удовлетворяющая условиям Дирихле (функция на интервале Т имеет конечное число разрывов и экстремумов). Такая функция может быть представлена суммой гармонических составляющих с различными амплитудами Е_n, частотами ω_n=nω₁ и начальными фазами φ_n в виде ряда Фурье

.

Ряд Фурье можно представить в другой форме:

.

Постоянная составляющая Е₀ и коэффициенты ряда Фурье В_n и С_n рассчитываются по формулам

Для нечетных функций е(t) коэффициенты С_n=0, а для четных B_n=0, Связь между коэффициентами B_n, C_n и амплитудами Е_n и фазами φ_n гармоник определяется соотношениями

.

Диаграмма, на которой изображают зависимость амплитуды гармоник E_n от частоты ω_n=nω₁, называют спектром.

Используя метод суперпозиции и спектральное представление периодической э.д.с. в виде ряда Фурье электрическую цепь можно рассчитать по следующей методике:

1. Несинусоидальная периодическая э.д.с. е(t) раскладывается в ряд Фурье и определяются амплитуды E_n и фазы φ_n всех гармоник э.д.с.

2. В интересующей ветви рассчитываются токи i₀, i₁,...i_n, создаваемые каждой гармоникой э.д.с.

3. Искомый ток в ветви находится как сумма токов

.

Так как составляющие тока i(t) либо постоянная величина i₀, либо синусоидальные токи i_n, то для их определения применяют известные методы расчета цепей постоянного и переменного синусоидального токов.

Рассмотрим примеры спектрального разложения наиболее распространенных периодических э.д.с.

1. Периодическая последовательность прямоугольных импульсов (рис.1).

Постоянная составляющая последовательности

,

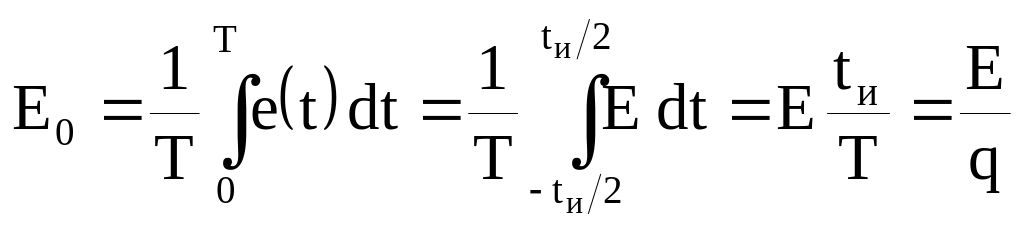где q=T/t_и – скважность импульсов.

Амплитуды гармоник с учетом четности функции e(t)

.

Ряд Фурье для последовательности прямоугольных импульсов будет иметь вид

.

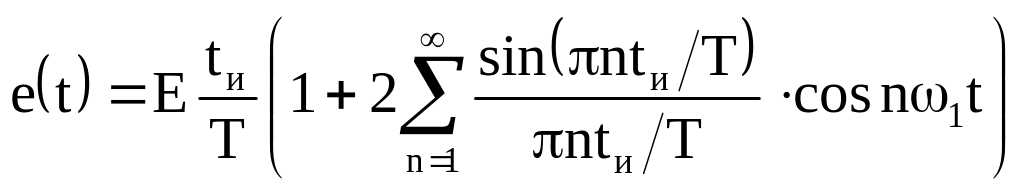А

Рис. 1. Периодическая последовательность прямоугольных импульсов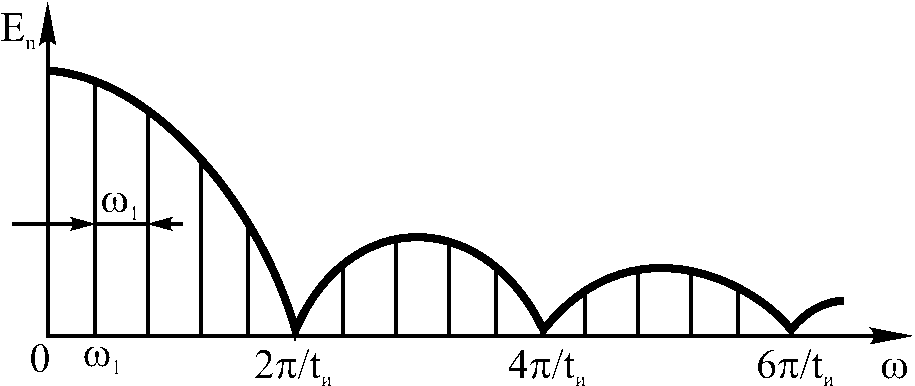

мплитудный спектр последовательности при скважности q=5 показан на рис.2. Спектры периодических функций дискретные.

О

Рис. 2. Спектр периодической последовательности прямоугольных импульсов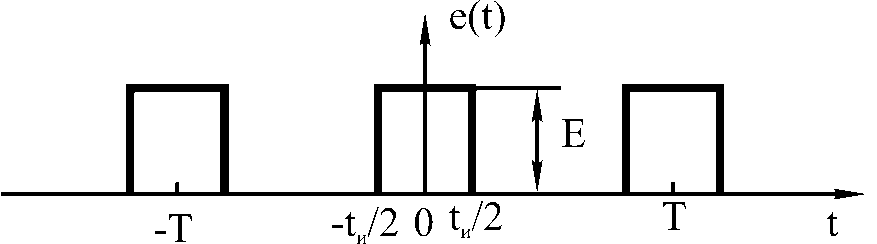

ни содержат составляющие с частотами n₁, кратными частоте основной гармоники ω₁=2π/T. Параметром спектров является их ширина ∆ω. Для последовательности прямоугольных импульсов за ширину спектра принимают протяженность главного максимума

∆ω = 2π/t_и.

Для импульсов простой формы произведение длительности импульсов на ширину спектра оказывается величиной постоянной

t_и·∆ω= 2π.

2. Периодическая последовательность импульсов косинусо-идальной формы. Такие импульсы могут быть получены при ограничении э.д.с. вида E_m·cosω₁t на уровне E=E_m·cos (рис.3). Аналитическая запись одного импульса последовательности имеет вид

,

г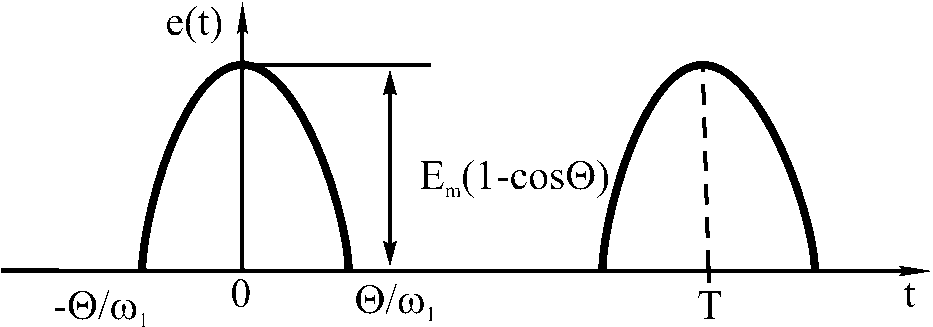 де =arccos E/E_m – угол отсечки.

П

Рис. 3. Периодическая последовательность косинусоидальных сигналов

остоянная составляющая и амплитуды гармоник спектра последовательности определяются по формулам

E_n=E_m·γ_n(), Eo = E_m·γ₀(),

где γ₀(), γ_n() – коэффициенты Берга. Зависимости первых трех коэффициентов Берга от угла отсечки показаны на рис.4.

3

Рис. 4. Зависимость первых трех коэффициентов Берга от угла отсечки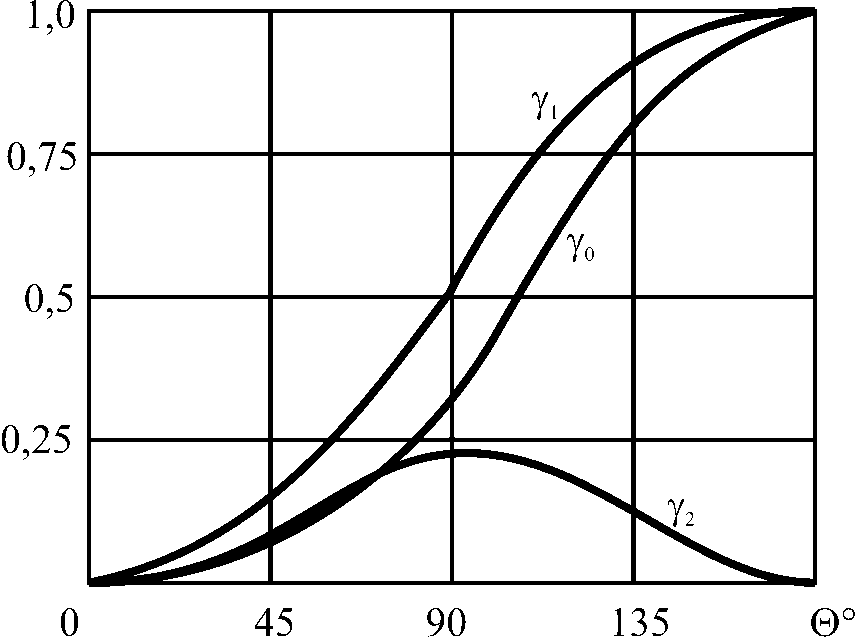

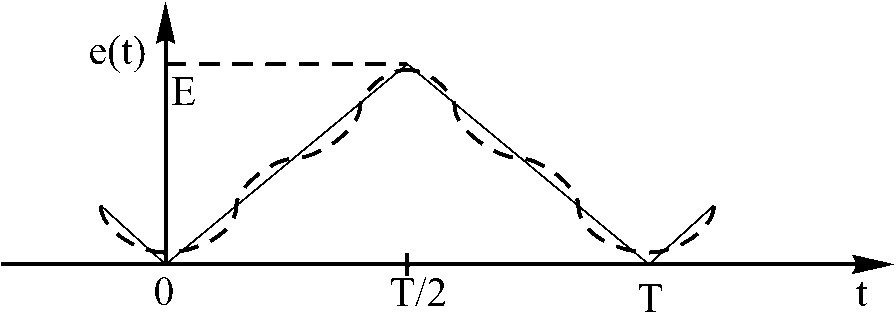
. Последовательность импульсов треугольной формы.

Один импульс последовательности описывается выражением

График треугольного колебания и сумма трех гармоник ряда Фурье для этой функции показаны на рис.5. Ряд Фурье для треугольных импульсов состоит из нечетных гармоник

.

С

Рис. 6. Спектр последовательности треугольных импульсов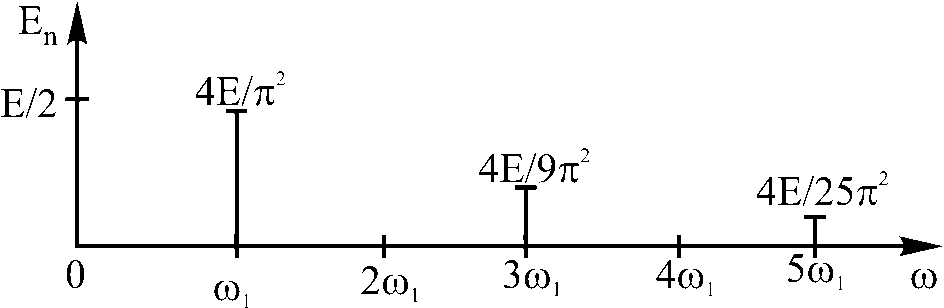

пектральная диаграмма последовательности изображена на рис.6.

Рис. 5. Периодическое колебание треугольной формы и сумма трех первых гармоник ряда Фурье (пунктирная линия)