
Комбинаторика
Билет 1
Правило сложения: Если элемент A можно выбрать n способами, а элемент B можно выбрать m способами, то выбрать A или B можно n + m способами.
Правило умножения: Если элемент A можно выбрать n способами, и при любом выборе A элемент B можно выбрать m способами, то пару (A, B) можно выбрать n·m способами. Естественным образом обобщается на произвольную длину последовательности.
Декартово произведение множеств.Множество А × В всех упорядоченных пар элементов (a, b), из которых a принадлежит множеству A, b — множеству B. Порядок следования пар может быть любым, но расположение элементов в каждой паре (векторе, кортеже) определяется порядком следования перемножаемых элементов. Поэтому A × B ≠ B × A, если B ≠ A.
Если обобщить сказанное на любое количество множеств A1, A2, ..., An, то Д. п. записывается так:

Если перемножаются одинаковые множества, используется обозначение степени:
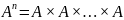
Множество
всех подмножеств множества
Пусть ![]() — множество.
Множество
всех подмножеств множества
называется булеаном
(также степенью
множества, показательным
множеством или
множеством
частей)
и обозначается
— множество.
Множество
всех подмножеств множества
называется булеаном
(также степенью
множества, показательным
множеством или
множеством
частей)
и обозначается ![]() или
или ![]() .
Ясно, что
.
Ясно, что ![]() и
и ![]() .
.
Если два множества равномощны, то равномощны и их булеаны. Справедливо следующее утверждение:
-
Число подмножеств конечного множества, состоящего из
 элементов,
равно
элементов,
равно  .
.
Доказательство проведем методом математической индукции.
База.
Если ![]() ,
т. е. множество пусто, то у него только
одно подмножество — оно само, и
интересующее нас число равно
,
т. е. множество пусто, то у него только
одно подмножество — оно само, и
интересующее нас число равно ![]() .
.
Индукционный
шаг.
Пусть утверждение справедливо для
некоторого n и пусть ![]() —
множество с мощностью
—
множество с мощностью ![]() .
Зафиксировав некоторый элемент
.
Зафиксировав некоторый элемент ![]() ,
разделим подмножества множества
на
два:
,
разделим подмножества множества
на
два:
 ,
содержащее
,
содержащее  ,
,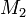 ,
не содержащее
,
то есть являющиеся подмножествами
множества
,
не содержащее
,
то есть являющиеся подмножествами
множества  .
.
Подмножеств типа (2) по предположению индукции . Но подмножеств типа (1) ровно столько же, так как подмножество типа (1) получается из некоторого и притом единственного подмножества типа (2) добавлением элемента и, следовательно, из каждого подмножества типа (2) получается этим способом одно и только одно подмножество типа (1).
Следовательно
имеем ![]() и
и ![]() .
По индукционному предположению
.
По индукционному предположению ![]() и
и ![]() .
Получаем
.
Получаем ![]() .
.
Формула
включения-исключения.
Например, в случае двух множеств ![]() формула
включений-исключений имеет вид:
формула
включений-исключений имеет вид:
![]()
В
сумме ![]() элементы
пересечения
элементы
пересечения ![]() учтены
дважды, и чтобы компенсировать это мы
вычитаем
учтены
дважды, и чтобы компенсировать это мы
вычитаем ![]() из
правой части формулы.
из
правой части формулы.
Th
(принцип включения-исключения).
Пусть ![]() — конечные
множества.
Формула включений-исключений утверждает:
— конечные
множества.
Формула включений-исключений утверждает:

Док-во:
Рассмотрим
произвольный элемент ![]() и
подсчитаем, сколько раз он учитывается
в правой части формулы включений-исключений[4].
и
подсчитаем, сколько раз он учитывается
в правой части формулы включений-исключений[4].
Если
элемент ![]() не
обладает ни одним из свойств
не
обладает ни одним из свойств ![]() ,
то в правой части формулы он учитывается
ровно 1 раз (в члене
,
то в правой части формулы он учитывается
ровно 1 раз (в члене ![]() ).
).
Пусть
элемент
обладает в
точности ![]() свойствами,
скажем
свойствами,
скажем ![]() .
Он дает по 1 в тех слагаемых суммы
.
Он дает по 1 в тех слагаемых суммы ![]() ,
для которых
,
для которых ![]() есть
подмножество
есть
подмножество ![]() ,
и 0 для остальных. Число таких подмножеств
по определению есть число
сочетаний
,
и 0 для остальных. Число таких подмножеств
по определению есть число
сочетаний ![]() .
Следовательно, вклад элемента
в
правую часть равен
.
Следовательно, вклад элемента
в
правую часть равен
![]()
При ![]() числа
сочетаний равны нулю. Оставшаяся сумма
в силу биномиальной
теоремы(бином
Ньютона) равна
числа
сочетаний равны нулю. Оставшаяся сумма
в силу биномиальной
теоремы(бином
Ньютона) равна
![]()
Таким
образом, правая часть формулы
включений-исключений учитывает каждый
элемент, не имеющий указанных свойств
точно по одному разу, а каждый элемент,
обладающий хотя бы одним из свойств —
нуль раз. Следовательно, она равна
количеству элементов, не обладающих ни
одним из свойств
,
то есть ![]() .
Что и требовалось доказать.
.
Что и требовалось доказать.
Число
сочетаний из
по ![]() равно биномиальному
коэффициенту
равно биномиальному
коэффициенту

При
фиксированном
производящей
функцией последовательности
чисел сочетаний ![]() ,
, ![]() ,
, ![]() ,
… является:
,
… является:

Двумерной производящей функцией чисел сочетаний является

Задача о беспорядках:
Классический
пример использования формулы
включений-исключений — задача
о беспорядках [4].
Требуется найти число перестановок ![]() множества
множества ![]() таких
что
таких
что ![]() для
всех
для
всех ![]() .
Такие перестановки называются беспорядками.
.
Такие перестановки называются беспорядками.
Пусть ![]() —
множество всех перестановок
—
множество всех перестановок ![]() и
пусть свойство
перестановки
выражается равенством
и
пусть свойство
перестановки
выражается равенством ![]() .
Тогда число беспорядков есть
.
Тогда число беспорядков есть ![]() .
Легко видеть, что
.
Легко видеть, что ![]() —
число перестановок, оставляющих на
месте элементы
—
число перестановок, оставляющих на
месте элементы ![]() ,
и таким образом сумма
,
и таким образом сумма ![]() содержит
содержит ![]() одинаковых
слагаемых. Формула включений-исключений
дает выражение для числа
одинаковых
слагаемых. Формула включений-исключений
дает выражение для числа ![]() беспорядков:
беспорядков:

Это соотношение можно преобразовать к виду
![]()
Нетрудно
видеть, что выражение в скобках является
частичной суммой ряда  .
Таким образом, с хорошей точностью число
беспорядков составляет
.
Таким образом, с хорошей точностью число
беспорядков составляет ![]() долю
от общего числа
долю
от общего числа ![]() перестановок:
перестановок:
![]()
Билет 2.
Опр
Если
 действительное
число, положим по определения
действительное
число, положим по определения

Обозначается
 и читается, как «n
факториал от x
вниз».
и читается, как «n
факториал от x
вниз».
Число всех отображений из одного множества в другое.
Пусть
даны множества
 , причем множество
, причем множество
 содержит
содержит
 элементов
элементов
 ,
а множество
,
а множество
 содержит
содержит
 элементов
элементов
 .
В этих терминах задача может быть
сформулирована следующим образом:
сколько существует функций (отображений)
, удовлетворяющих заданным ограничениям.
Элементы множества
соответствуют
объектам, элементы множества
.
В этих терминах задача может быть
сформулирована следующим образом:
сколько существует функций (отображений)
, удовлетворяющих заданным ограничениям.
Элементы множества
соответствуют
объектам, элементы множества
 "ящикам" а каждая функция
"ящикам" а каждая функция
 определяет некоторое размещение,
указывая для каждого объекта
определяет некоторое размещение,
указывая для каждого объекта
 "ящик"
"ящик" , в котором данный объект находится.
, в котором данный объект находится.
Лемма
.
Если
 ,
то количество всех функций
равно
,
то количество всех функций
равно
 .
Эквивалентное
утверждение. Число слов длины n
в алфавите из
символов равно
.
.
Эквивалентное
утверждение. Число слов длины n
в алфавите из
символов равно
.
Док-во.
Без потери общности можно всегда считать,
что
 .
Каждую функцию можно тогда отождествить
с последовательностью
.
Каждую функцию можно тогда отождествить
с последовательностью
 .
Каждый член
.
Каждый член
 последовательности можно выбрать m
способами, что дает
возможностей выбора последовательности
последовательности можно выбрать m
способами, что дает
возможностей выбора последовательности
 (чтд)
(чтд)
Число инъективных отображений.
Опр
Отображение
 инъективно,
если
инъективно,
если

Лемма.
Число инъективных отображений (инъекций)
множества
из
элементов, ,
во множество
из
элементов,
,
во множество
из
элементов,
 есть
есть
 Эквивалентное
утверждение. Число слов длины
без повторений букв в алфавите из
букв есть
Эквивалентное
утверждение. Число слов длины
без повторений букв в алфавите из
букв есть
 .
.
Док-во.
Будем определять на этот раз число
инъективных, (то есть имеющих все
различные члены) последовательностей
 .
Элемент
.
Элемент
 может быть выбран
способами, элемент
может быть выбран
способами, элемент
 можно выбрать
можно выбрать
 способом из оставшихся элементов. В
общем случае, если уже выбраны элементы
способом из оставшихся элементов. В
общем случае, если уже выбраны элементы
 ,
то в качестве
может быть выбран любой из
,
то в качестве
может быть выбран любой из
 элементов множества
элементов множества
 .
(Принимаем, что
.
(Принимаем, что
 ,
если
,
если
 ,
то и
и искомое число функций равно 0). Это
дает
,
то и
и искомое число функций равно 0). Это
дает
 возможность выбора инъективных
последовательностей
.
возможность выбора инъективных
последовательностей
.

(чтд)
Возрастающие и убывающие субфакториалы.
Возрастающий субфакториал числа n (обозначение: !n) определяется как количество беспорядков порядка n, то есть перестановок порядка n без неподвижных точек. Название субфакториал происходит из аналогии с факториалом, определяющим общее количество перестановок.
В частности, !n есть число способов положить n писем в n конвертов (по одному в каждый), чтобы ни одно не попало в соответствующий конверт
Явная формула
Субфакториал можно вычислить с помощью принципа включения-исключения:


 (таким
же свойством обладает сам факториал)
(таким
же свойством обладает сам факториал)
Убывающий субфакториал:
Опр Если действительное число, положим по определения
Обозначается и читается, как «n факториал от x вниз».
Перестановки ,размещения и сочетания.
Будем
обозначать через
 множество из
элементов. Без ограничения общности
можно считать, что
множество из
элементов. Без ограничения общности
можно считать, что

Опр.
Перестановкой
множества
M называется произвольная биекция
 Очевидно, что для n-элементных множеств
количество всевозможных перестановок
равно
Очевидно, что для n-элементных множеств
количество всевозможных перестановок
равно
 .
.
Опр.
Назовём размещением из n элементов по
k любое упорядоченное множество
 , где
, где
 .
Количество всевозможных размещений из
элементов по
.
Количество всевозможных размещений из
элементов по
 обозначается
обозначается
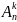
Утверждение 1. Справедливо равенство

Док-во:
Первый из k элементов можно выбрать n
способами, второй
 способом, и т. д. Последний,
способом, и т. д. Последний,
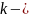 й
элемент, можно выбрать
й
элемент, можно выбрать
 способами. Поэтому число размещений
равно указанному произведению (чтд)
способами. Поэтому число размещений
равно указанному произведению (чтд)
Опр.
Сочетание - это неупорядоченное
размещение. Говоря более формально,
сочетание из
элементов по
это произвольное подмножество
 элементного
множества. Количество сочетаний из
элементов по
обозначается
элементного
множества. Количество сочетаний из
элементов по
обозначается
 или
или
 .
.
Утверждение 2. Справедливо равенство

Док-во:
Рассмотрим произвольное сочетание.
Всевозможными перестановками из него
можно получить
 различных размещений, причём для разных
сочетаний получаются, естественно,
непересекающиеся наборы размещений.
Это означает, что количество размещений
в
больше числа сочетаний.(чтд)
различных размещений, причём для разных
сочетаний получаются, естественно,
непересекающиеся наборы размещений.
Это означает, что количество размещений
в
больше числа сочетаний.(чтд)
Ясно, что

Из
последней формулы очевидно, что
 .
У этой формулы
есть и другое обоснование: существует
биекция между
элементными
подмножествами и их
.
У этой формулы
есть и другое обоснование: существует
биекция между
элементными
подмножествами и их
 элементными
дополнениями.
элементными
дополнениями.
Число подмножеств данной мощности.
-
Число подмножеств конечного множества, состоящего из элементов, равно .
Доказательство проведем методом математической индукции.
База. Если , т. е. множество пусто, то у него только одно подмножество — оно само, и интересующее нас число равно .
Индукционный шаг. Пусть утверждение справедливо для некоторого n и пусть — множество с мощностью . Зафиксировав некоторый элемент , разделим подмножества множества на два:
, Содержащее ,
, Не содержащее , то есть являющиеся подмножествами множества .
Подмножеств типа (2) по предположению индукции . Но подмножеств типа (1) ровно столько же, так как подмножество типа (1) получается из некоторого и притом единственного подмножества типа (2) добавлением элемента и, следовательно, из каждого подмножества типа (2) получается этим способом одно и только одно подмножество типа (1).
Следовательно имеем и . По индукционному предположению и . Получаем .
Формула включения-исключения. Например, в случае двух множеств формула включений-исключений имеет вид:
В сумме элементы пересечения учтены дважды, и чтобы компенсировать это мы вычитаем из правой части формулы.
Th (принцип включения-исключения). Пусть — конечные множества. Формула включений-исключений утверждает:
Док-во: Рассмотрим произвольный элемент и подсчитаем, сколько раз он учитывается в правой части формулы включений-исключений[4].
Если элемент не обладает ни одним из свойств , то в правой части формулы он учитывается ровно 1 раз (в члене ).
Пусть элемент обладает в точности свойствами, скажем . Он дает по 1 в тех слагаемых суммы , для которых есть подмножество , и 0 для остальных. Число таких подмножеств по определению есть число сочетаний . Следовательно, вклад элемента в правую часть равен
При числа сочетаний равны нулю. Оставшаяся сумма в силу биномиальной теоремы(бином Ньютона) равна
Таким образом, правая часть формулы включений-исключений учитывает каждый элемент, не имеющий указанных свойств точно по одному разу, а каждый элемент, обладающий хотя бы одним из свойств — нуль раз. Следовательно, она равна количеству элементов, не обладающих ни одним из свойств , то есть . Что и требовалось доказать.
Перестановки с повторениями.
Опр
Последовательность длины
,
составленная из
разных
символов, первый из которых повторяется  раз,
второй —
раз,
второй —  раз,
третий —
раз,
третий —  раз,…,
й
—
раз,…,
й
—  раз
раз
 называется перестановкой
с повторениями из
элементов.
называется перестановкой
с повторениями из
элементов.
Например,
пусть дан набор из четырех букв  .
Тогда все перестановки с повторениями
из этих букв суть
.
Тогда все перестановки с повторениями
из этих букв суть  .
Число перестановок с повторениями
длины n из k разных
элементов, взятых соответственно
по n1, n2,
…, nk раз
каждый обозначается
.
Число перестановок с повторениями
длины n из k разных
элементов, взятых соответственно
по n1, n2,
…, nk раз
каждый обозначается

Полиномиальные коэффициенты и полиномиальная теорема.
Мультиномиальные (полиномиальные) коэффициенты —
коэффициенты в разложении ![]() по мономам
по мономам ![]() :
:

Значение
мультиномиального коэффициента ![]() определено
для всех целых неотрицательных
чисел n и
определено
для всех целых неотрицательных
чисел n и ![]() таких,
что
таких,
что ![]() :
:
![]()


Билет 3
Мультимножества и число мультимножеств данной мощности.
Мультимножество — в математике, обобщение понятия множества, допускающее включение одного и того же элемента по нескольку раз.
Число элементов в мультимножестве, с учетом повторяющихся элементов, называется его размером или мощностью.
