
Пример по выводу уравнений колебаний.
В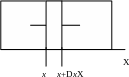 ыведем
волновое уравнение на примере продольных
волн деформации в стержне. Если
возвращающая сила пропорциональна
смещению точки от положения равновесия,
то волна называется упругой.
Выделим часть стержня длиной Dx.
Если площадь поперечного сечения стержня
равна S,
плотность материала r,
то масса этой части
ыведем
волновое уравнение на примере продольных
волн деформации в стержне. Если
возвращающая сила пропорциональна
смещению точки от положения равновесия,
то волна называется упругой.
Выделим часть стержня длиной Dx.
Если площадь поперечного сечения стержня
равна S,
плотность материала r,
то масса этой части
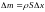 .
При деформациях на эту часть стержня
действую силы упругости. Запишем второй
закон Ньютона – уравнение движения
этой части стержня вдоль оси Х:
.
При деформациях на эту часть стержня
действую силы упругости. Запишем второй
закон Ньютона – уравнение движения
этой части стержня вдоль оси Х:
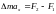 .
.
Это уравнение
записано в предположении растяжения
этой части стержня. Силы с обеих сторон
выделенной части вызваны деформацией
стержня. При равновесии и отсутствии
деформации положение точек в двух близко
расположенных сечениях стержня можно
задать координатами x
и x+Dx.
А при деформировании стержня его точки
сместятся от равновесных положений.
Пусть x1(x)
– задает положение точки стержня при
деформации, если её равновесное положение
задавалось координатой x.
Тогда для близкого сечения новыми
координатами будет x1+Dx1.
Изменение линейного размера части
стержня вызвано смещением точек стержня.
Введем величину смещения x=
x1
-
x.
По определению, относительная деформация
в данном сечении стержня – это отношение
изменения длины части стержня к начальной
длине этой части:
 .
Если стержень сжимается, то его продольные
размеры уменьшаются
.
Если стержень сжимается, то его продольные
размеры уменьшаются
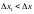 и поэтому e<0.
Таким образом, при сжатии e<0
и при растяжении e>0.
и поэтому e<0.
Таким образом, при сжатии e<0
и при растяжении e>0.
Если все точки
стержня смещаются на одинаковую величину,
то изменения длины участка стержня не
происходит. Поэтому деформация равна
разности смещений соседних точек
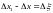 .
Тогда можно записать
.
Тогда можно записать
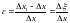 .
В пределе (при
.
В пределе (при
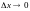 )
получаем
)
получаем
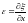 .
.
По обобщенному
закону Гука
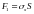 ,
,
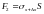 .
Напряжения в сечениях стержня найдем
по закону Гука:
.
Напряжения в сечениях стержня найдем
по закону Гука:
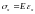 ,
,
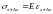 ,
где Е
– модуль упругости материала (модуль
Юнга).
,
где Е
– модуль упругости материала (модуль
Юнга).
Относительная
деформация меняется вдоль стержня,
поэтому можно считать, что
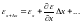 (разложение в ряд Тейлора). Ускорение
точек выделенной части стержня
(разложение в ряд Тейлора). Ускорение
точек выделенной части стержня
 .
Последовательно подставим эти соотношения
в уравнения движения:
.
Последовательно подставим эти соотношения
в уравнения движения:
:
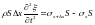 ,
,
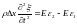 ,
,
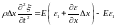 ,
,
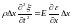 .
.
С учетом равенства , после сокращений, получаем дифференциальное уравнение, описывающее распространение волны (вдоль одного направления – оси Х):
.
Здесь, x
- параметр, описывающий колебания
(величина смещения точек при деформации),
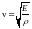 – скорость волны.§
– скорость волны.§
Рассмотрим выделенный
участок стержня длиной Dx,
во всех точках
которого можно считать одинаковыми
величину деформации
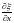 и скорость частиц среды
и скорость частиц среды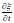 .
Соответственно, кинетическая и
потенциальные энергии выделенного
участка равны
.
Соответственно, кинетическая и
потенциальные энергии выделенного
участка равны
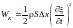 и
и
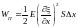 .
Объем участка
.
Объем участка
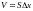 .
Объемная плотность механической энергии
.
Объемная плотность механической энергии
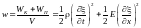 .
.
Если уравнение
движения волны записать в виде
 ,
то с учетом соотношений для скорости
,
то с учетом соотношений для скорости
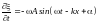 и деформации
и деформации
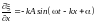 получается
получается
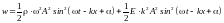 ,
,
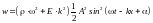 .
.
В каждой точке среды объемная плотность механической энергии изменяется во времени как квадрат синуса.
Используем выражение
для скорости волны
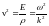 :
:
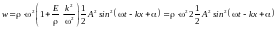 ,
,
 .
.
Среднее значение плотности потока энергии, переносимой волной
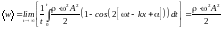 .
.
Следствия
Величины скорости точек среды и деформации среды колеблются синфазно друг другу.
Закон изменения плотности энергии описывается волновым уравнением и представляет волну плотности энергии. Скорость этой волны
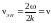 в данном случае совпадает с фазовой
скоростью волны. (В общем случае это не
так.)
в данном случае совпадает с фазовой
скоростью волны. (В общем случае это не
так.)
