Екзаменаційний білет № 1

1. Числова послідовність та її границя.

Числовою послідовністю (x_n) наз. відображення NR: nx_n, т.т. ф-ція, яка кожному натуральному числу n ставить у відповідність деяке дійсне число x_n.

Послідовність дійсних чисел (x_n) наз. збіжною, якщо aR: 0 N_: nN_  x_n - a<. Число a наз. границею послідовності (x_n) і позначається lim x_n=a, n або x_na при n. Якщо a=0, то послідовність (x_n) наз. нескінченно малою і позначається o(1). Якщо 1x_n=o(1), то послідовність (xn) наз. нескінченно великою і позначається lim x_n= , n. Якщо послідовність немає границі, то вона наз. розбіжною.

Якщо для послідовності (x_n) C: nN  x_n<C, то послідовність наз. обмеженною і позначається O(1). Символи o(1) та O(1) наз. символами Ландау.

Теорема 1. Нехай посл-ть x_n- збігається тоді 1){x_n}- обмежена, 2){x_n}- має єдину границю, 3) {x_n} збігається до а <=> якщо для 0 т.а містить всі члени {x_n}єU(a)( околу) nN за винятком можливого скінченого її числа.

Теорема 2. (про зб. ч. посл-тей)1) (x_nа, n)^ (y_nb, n)=>(x_n+y_nа+b, n); 2) (x_nа, n)^(y_nb, n)=>(x_ny_nаb, n); 3) (x_nа, n)^(x_nне=0,nN)^(a не=0)=>(1/x_n1/а, n);

Теорема 3. (про гран. перехід нер-тей)

x_nа, n, bєR: b>a n₀єN: x_n<b n>n₀;

Теорема 4. (x_nа, n)^(x_n=<b nєN)=>(a<=b);

Теорема 5. (x_nа, n)^ (z_na, n)^(x_n=<y_n =<z_n nєN)=>(y_nа, n);

Монотонні посл-ті:

{x_n}-неспадна, x_n=<x_n+1, nєN; {x_n}-незростаюча, x_n>=x_n+1, nєN; {x_n}-зростаюча, x_n<x_n+1, nєN; {x_n}-спадна, x_n>x_n+1, nєN;

Теорема (про границю монотонних посл-тей)

1) неспадна (зростаюча) обмежена зверху числ посл. збігається; 2) незростаюча (спадна) обмежена знизу числ посл. збігається.

Теорема 1. lim x_n= a  x_n= a+o(1), n, aR

Необхідність: нехай а - границя послідовності x_n. >0 N; n>N xn-a< x_n-a=_n >0 N, n>N _n<. _n -нескінчено мала  _т=о(1)  x_n-a=o(1)

Достатність: x_n-a=o(1) доведемо, що Lim x_n=a, n. x_n-a=_n  _n=o(1)  _n -нескінчено мала. >0 N, n>N _n<  x_n-a<  Lim x_n=a, n

Підпослідовності: Посл. {y_n} елементів множ Е визнач рівністю y_n=x_nk, kєN наз підпосл-тю посл-ті x_n і познач {х_nk}, коротко познач-ся {х_nk}є {х_n}.

Теорема. Посл {х_n}а, n  коли всі її підпосл {х_nk}а, n для {х_nk}є {х_n}.

Озн. Нехай {х_n}– деяка посл-ть, а {х_nk}– її підпосл, яка має границею а при k, тоді а – часткова границя посл {х_n}.

Теорема. Нехай {х_n} ЧП, що прямує до а при n в R, тоді х_nk також прямує до а при n в R для {х_nk}є {х_n}.

Теорема Больцана-Вейєрштрасса.

З довільної обмеженої посл-ті можна виділити збіжну підпос-ть.

Теорема 2 (дії над символами Ландау).

1. O(1)+O(1)=O(1)

2. o(1)+o(1)=o(1)

_n, _n -неск. малі >0 N₁: n>N₁ _n</2 (1); >0 N₂: n>N₂ _n</2 (2) N=max{N₁;N₂} n>N виконується (1) і (2) _n_n_n+_n</2+/2= n>N  o(1)+o(1)=o(1)

3. O(1)*O(1)=O(1)

4. O(1)*o(1)=o(1)

x_n -обмежена величина, _n -неск. мала C>0: x_nC для n=1,2,...  (/C) N, n>N _n</C x_n*_n=x_n*_n<C*(/C)=, n>N  O(1)*o(1)=o(1)

1. _n<C*(/C)=, n>N  O(1)*o(1)=o(1)

Наслідок.

Якщо x_na, y_nb при n, (x_ny_n)ab, то (x_n*y_n)a*b, (x_n/y_n)a/b (якщо nN y_n  b).

Теорема 3 (критерій Коші).

Послідовність (x_n) збіжна тоді і тільки тоді, коли вона фундаментальна, тобто 0 n₀()єN: nn₀, pN  |x_n+p-x_n|<.

Верхня та нижня границя ЧП: а*-верхня границя {x_n}, а*= ; -нижня границя {a_n},

Теорема. 1) а*є Е, є Е; 2) якщо а*є R, то x>a* n₀єN: a_n<x,n>n₀, якщо 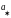є R, то x< n₀єN: a_n>x,n>n₀. При цьму а*( ) є ! елем для якого викон умови 1) та 2).

Теорема (критерій збіжності ЧП)

(ЧП {a_n}-збігається)(({a_n}- обмежена)^(а*= ))

Теорема Тьопліца Нехай 1) x_nа, n (aєR) 2) х_nk>=0, nєN, k=1,…,n 3) nєN 4) х_nk0, n kєN Тоді .

Теорема Штольца Нехай {x_n},{y_n}-ЧП 1) y_n<y_n+1 nєN 2) y_n, n 3)  lim (x_n-x_n-1/y_n-y_n-1)=l при n в R Тоді  lim (x_n/y_n)=l при n.