1Плоский случай

         Пусть дан криволинейный интеграл второго рода по плоской кривой

.

Ответ на поставленный вопрос дают следующие две теоремы.

         Теорема 1. Для того чтобы   не зависел от пути интегрирования необходимо и достаточно, чтобы существовала такая функция  , что

.

         Теорема 2. Если в односвязной области существуют и непрерывны 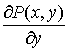  и  , то для того, чтобы было выполнено условие теоремы 1, необходимо и достаточно, чтобы

.

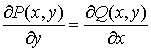2Пространственный случай

         В случае интегралов по пространственной кривой соответствующие теоремы приобретают следующий вид.

         Теорема 1. Для того чтобы   не зависел от пути интегрирования необходимо и достаточно, чтобы существовала такая функция,   что  .

         Для формулировки второй теоремы введем понятие ротора векторной функции. Пусть   . Тогда ротор этой функции определяется так:

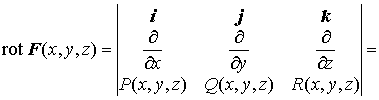
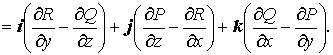
Теорема 2. Для того чтобы   не зависел от пути интегрирования необходимо и достаточно, чтобы выполнялось условие

. 

4.2 физический смысл криволинейного интеграла второго типа

Физический смысл

         Рассмотрим криволинейные интегралы второго рода по пространственной кривой

.

Рассмотрим так называемую вектор-функцию

как трехмерный вектор с компонентами  ,    и  , а также вектор  . Тогда комбинация, стоящая под знаком интеграла, есть не что иное, как скалярное произведение   и  , то есть

,

и поэтому

.

         Физически вектор-функция   ассоциируется с силовым полем, когда в каждой точке пространства на материальную точку действует сила  . Примером такого поля может служить гравитационное поле, электрическое поле, магнитное поле и т.д. Физически скалярное произведение   имеет смысл работы, которую силовое поле   совершает, перемещая материальную точку по вектору dr. Поэтому, с точки зрения физика, криволинейный интеграл второго рода

есть работа, которую совершает силовое поле  , перемещая материальную точку по кривойАВ.

         Обозначим через a, b и g углы, которые вектор   образует с осями OX, OY и OZ. Заметим, что длина вектора 

есть не что иное, как дифференциал длины дуги кривой. Поэтому

и мы можем записать

.

Заметим, что слева стоит криволинейный интеграл второго рода, а справа – криволинейный интеграл первого рода. Эта формула, таким образом, дает связь между криволинейными интегралами первого и второго рода.

4.4 Нахождение функции по ее полному дифференциалу

5.2 Определение суммы ряда.Необходимый признак сходимости ряда Определение

Пусть   — числовой ряд. Число   называется  -ой частичной суммой ряда  .

Сумма (числового) ряда — это предел частичных сумм  , если он существует и конечен. Таким образом, если существует число  , то в этом случае пишут  . Такой ряд называется сходящимся. Если предел частичных сумм не существует или бесконечен, то говорят, что ряд расходится.

Необходимый признак сходимости ряда

Ряд     может сходиться лишь в том случае, когда член   (общий член ряда) стремится к нулю:

Это необходимый признак сходимости ряда (но не достаточный!). Если же общий член ряда не стремится к нулю — это достаточный признак расходимости.

[править]Примеры

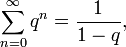•  где 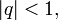  — сумма геометрической прогрессии, в частности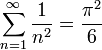

  • 

• .

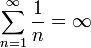•  — гармонический ряд расходится.

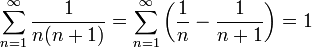•  — телескопический ряд.