§83. Вычеты и их приложения.
Коэффициент a-1 в лорановском разложении однозначной аналитической функции в окрестности конечной изолированной особой точки z0
,
называется
вычетом
этой функции
относительно точки z0
и
обозначается
(начальные
буквы res
от французского слова residu
– остаток).
Вычет через интеграл выражается формулой:
,
где
-
окружность,
В частном случае, когда z0 – полюс функции , вычет можно также вычислить по формуле:
,
если z0 – простой полюс, и по формуле:
,
если z0 – полюс кратности m>1.
Вычет в устранимой особой точке равен нулю.
В задачах 2873-2886 требуется найти вычеты указанны функций относительно ее конечных изолированных особых точек.
№2873.
Решение
Очевидно, z=0 и z=1 являются простыми полюсами, т.к.
,
значит
№2874.
Решение
z=2, z=-i.
- простые полюсы
Тогда
№2875.
Решение
- простые полюсы
№2876.
Решение
- простые полюсы
№2877.
Решение
- полюсы второй
кратности
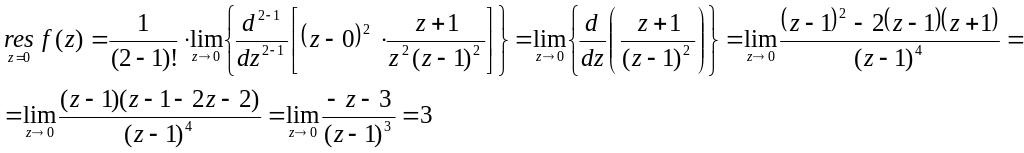
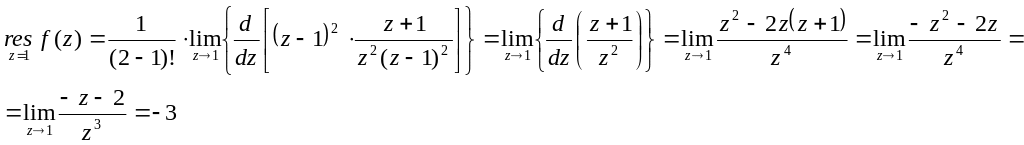
№2878.
Решение
- простые полюсы
№2879.
Решение
- полюс третьей
кратности
- полюс второй
кратности
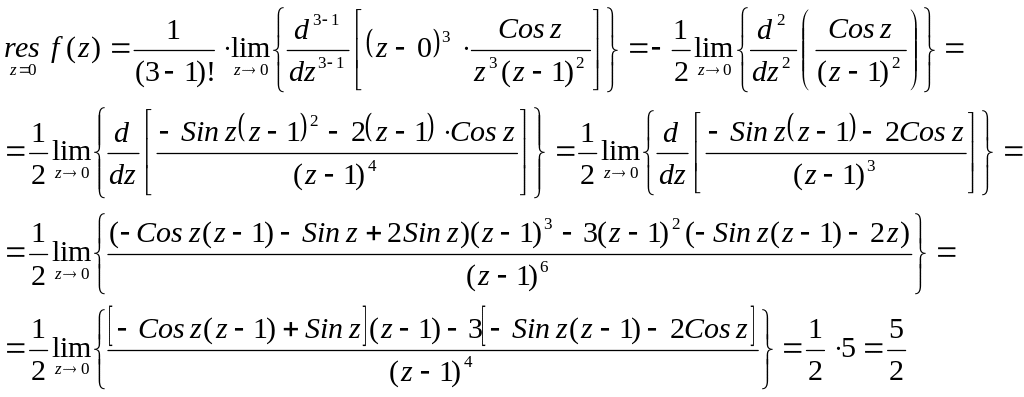
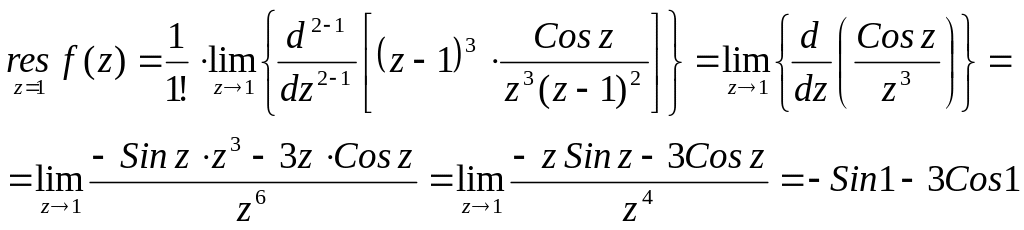
№2880.
Решение
- полюс второй
кратности
- простые полюсы
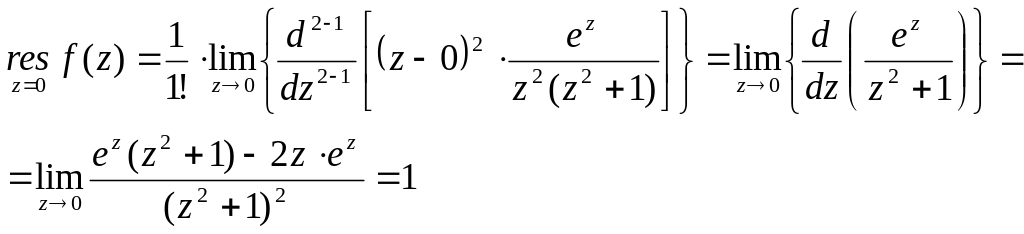
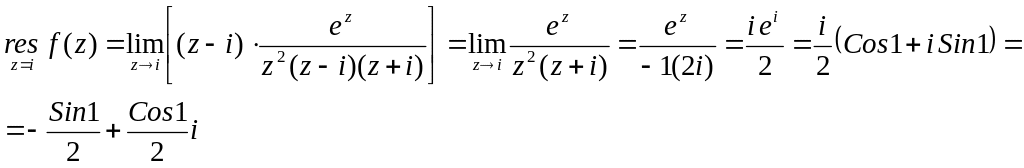
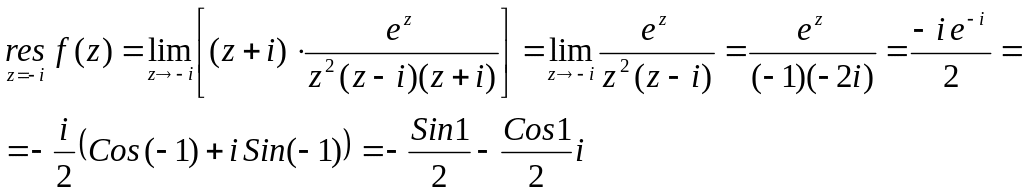
№2881.
Решение
- простые полюсы
№2882.
Решение
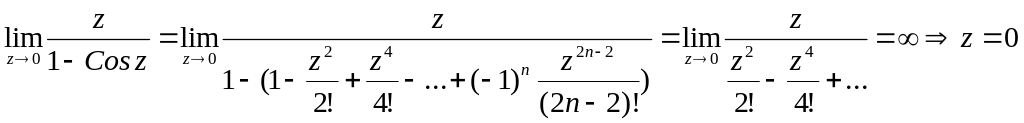простой полюс
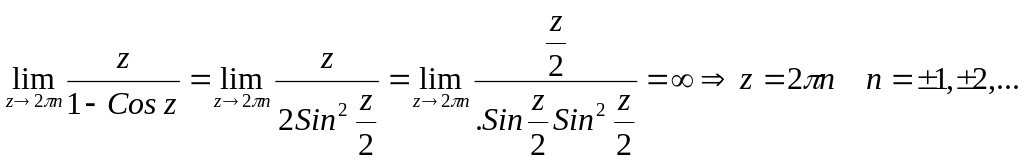- простые полюсы
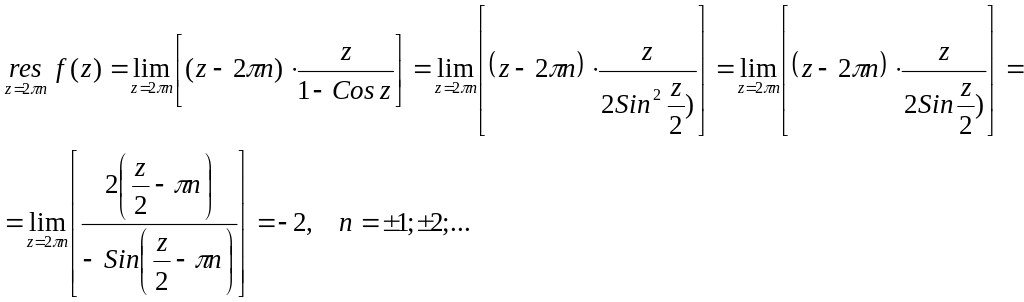
Интеграл от
функции
по кусочно-гладкому контуру Жордина L,
лежащему в области D,
где функция
однозначна и аналитична, кроме конечного
числа изолированных особых точек
,
равен произведению суммы вычетов функции
относительно ее особых точек, лежащих
внутри L,
на 2πi,
т.е.:
Вычислить интегралы в задачах 2890-2899.
№2890.
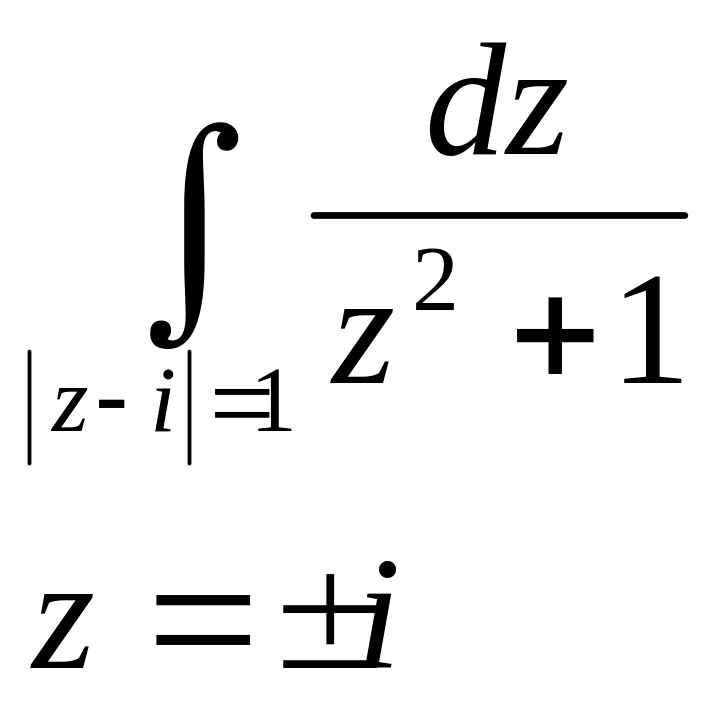
- простые полюсы
Очевидно, что в круг радиуса 1 с центром в точке i попадает точка i следовательно по теореме Коши о вычетах
(Сумма состоит из одного слагаемого, т.к. z=-i не лежит внутри L)
тогда
№2891.
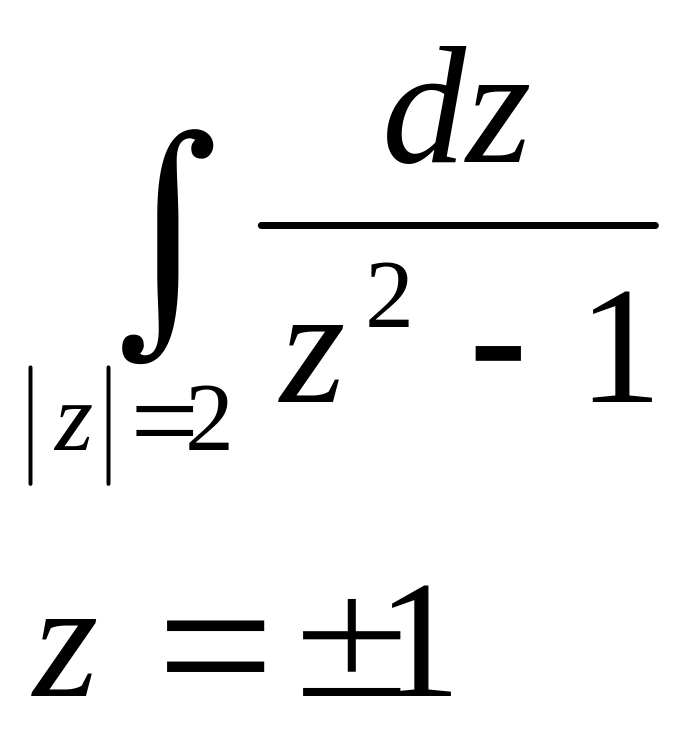
- простые
полюсы.
Обе точки лежат внутри L.
тогда
№2892.
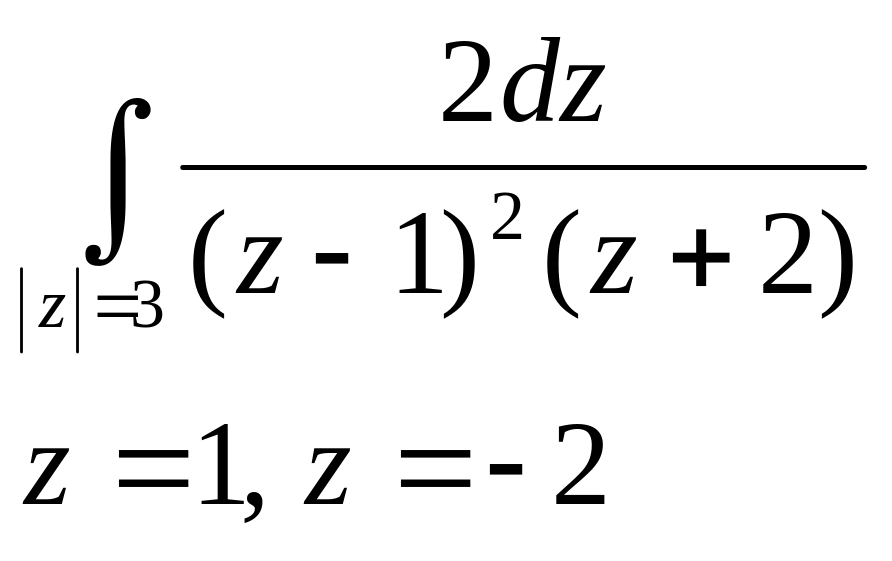
Обе точки лежат внутри L.
- полюс второй
кратности
- простой полюс
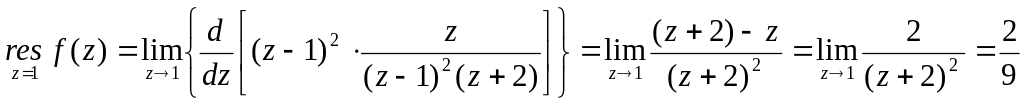
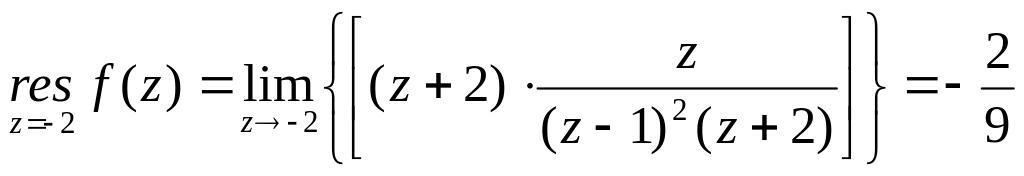
Тогда
№2893.
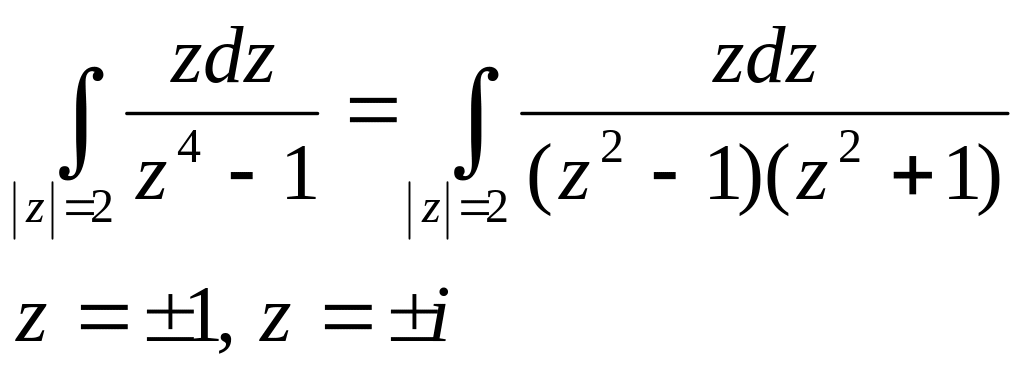
Все они лежат внутри L.
- простые полюсы
Тогда
№2894.
не существует,
следовательно z=0
– существенно особая точка.
(коэффициент при
z-1)
Тогда
№2895.
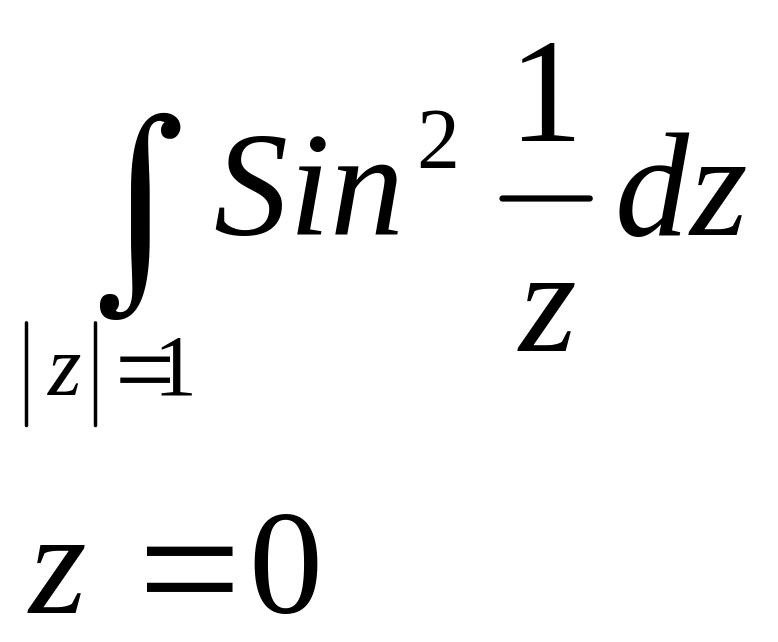
(существенно особая точка)
№2896.
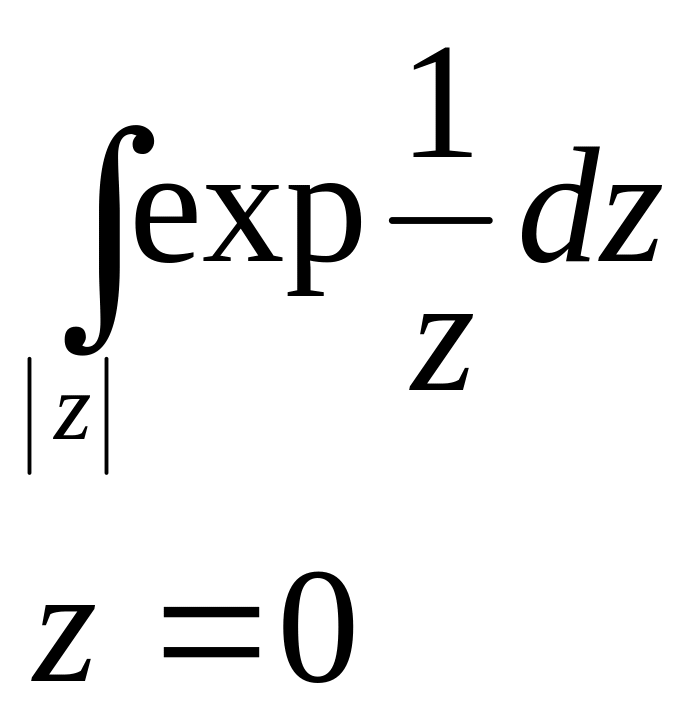
- существенно
особая точка.
№2897.
Найдем лорановское разложение:
коэффициент при z -1 не равен нулю и таких отличных от нуля коэффициентов бесконечное множество, следовательно точка z=0 – существенно особая точка и
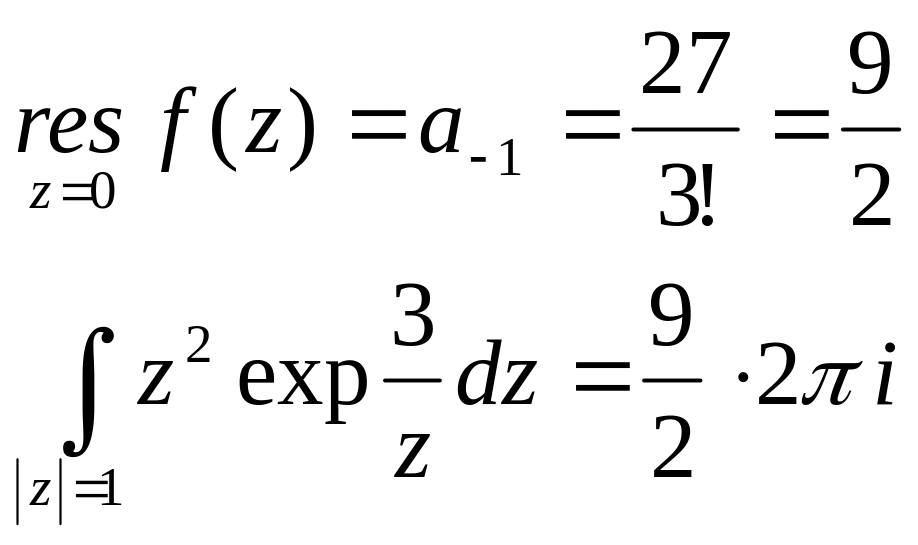
№2898.
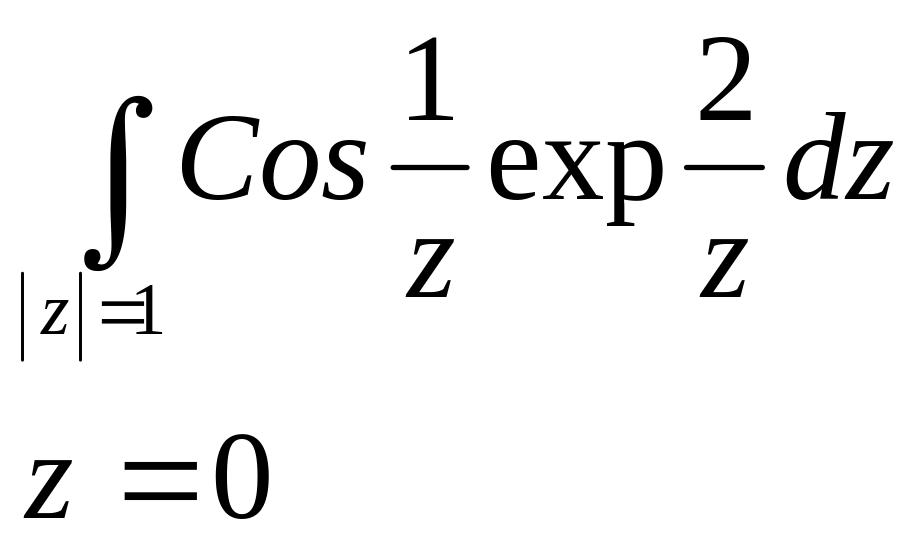
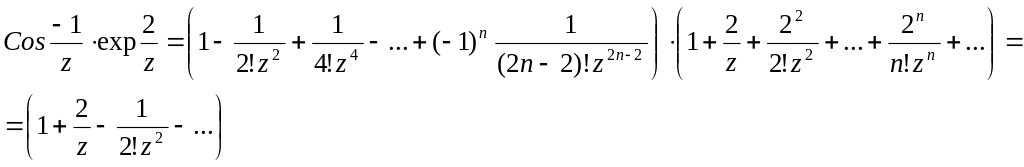
коэффициент при z-1 не равен нулю и таких отличных от нуля коэффициентов бесконечное множество, следовательно точка z=0 – существенно особая точка и
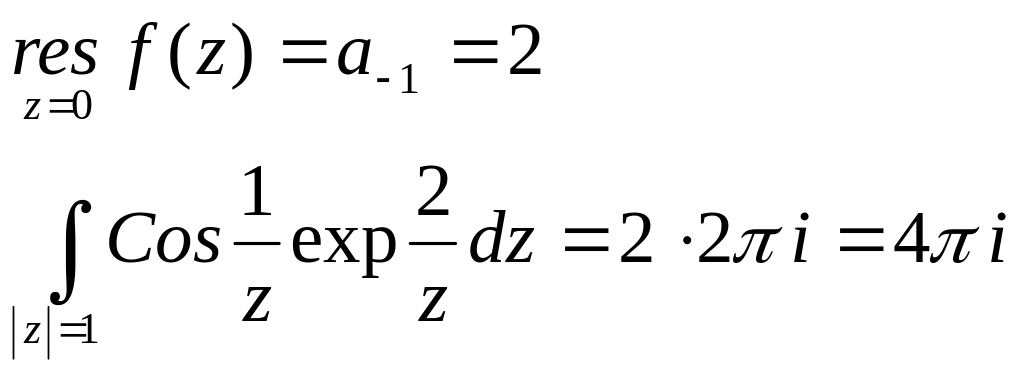
Пусть дробно-рациональная функция
не имеет полюсов
на действительной оси, причем степень
многочлена Qm(z)
по крайней мере на две единицы превышает
степень многочлена Pm(z)
.
Тогда
где суммы вычетов распространяются на те полюсы функции f(z), которые содержатся в верхней полуплоскости.