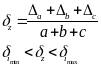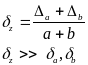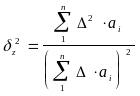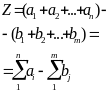6.5.Учет не исключенных систематических погрешностей

На практике систематическая погрешность очень часто включает несколько составляющих и в том числе так называемые не исключенные остатки систематической погрешности, т.е. погрешности оставшиеся после введения поправок.

К числу не исключенных систематических погрешностей относятся следующие:

6.5.1. Погрешности, связанные с точностью определения поправок.

6.5.2. Погрешности, зависящие от точности измерения влияющей величины, входящей в формулу определения поправок.

6.5.3. Погрешности, связанные с колебанием влияющих величин при невозможности их контроля и учета поправок.

6.5.4.Методические или теоретические погрешности.

6.5.5. Погрешности, связанные с округлением при снятии показаний СИ.

6.5.6. Погрешности поверки и калибровки средств измерений и др.

Для каждого данного измерения, не исключенные остатки систематической погрешности имеют вполне определенные значения, но эти значения нам неизвестны. Известно лишь, что в массе однократных измерений эти остатки лежат в определенных границах или имеют определенное среднее квадратическое отклонение, не превышающие , где к - номер не исключенной составляющей систематической погрешности. Если закон распределения не исключенной систематической погрешности неизвестен, то для самих систематических погрешностей _к принимают равномерный закон распределения, а для - нормальный. Дисперсия суммы не исключенных остатков систематической погрешности (НСП) определяется как сумма дисперсий не исключенных остатков:

. . . . . . . . .(6.42),

где m₁ - число систематических погрешностей, заданных границами _kmax,

m₂ - число систематических погрешностей, заданных СКО .

Не все составляющие НСП играют одинаковую роль или вносят одинаковый вклад в суммарную НСП. Отдельные составляющие вносят пренебрежительно малый вклад в суммарную погрешность, и ими можно пренебречь. Пользуясь правилами округления и, учитывая, что погрешность выражается не более чем двумя значащими цифрами, можно ввести такое условие, при котором можно пренебречь к-ой составляющей НСП:

. . . . . . . . . . (6.43),

где - суммарная погрешность результата измерения.

Значение 1,05 получено из условия округления 1,049999...

. . . . . . . . . . . . (6.44);

для исключения погрешностей должно выполняться условие:

т.е. или .

Это условие легко распространяется на случай нескольких составляющих, которыми можно пренебречь:

. . . . . . . . .(6.45).

Контрольные вопросы

1. Что понимается под «неисколюченными систематическими погрешностями»?

2.Какие систематические погрешности невозможно исключить полностью?

3. Как определяется дисперсия суммы НСП?

4. Каково условие, при котором можно пренебречь НСП?

6.6. Правила и погрешности округления результатов наблюдений и вычислений

Точность результатов наблюдений и последующих вычислений при обработке данных должны быть согласованы с необходимой точностью результатов измерений. Погрешность результатов измерений следует выражать не более чем двумя значащими цифрами. Две значащие цифры следует давать в двух случаях:

• При проведении высокоточных наблюдений.

• Если погрешность выражена числом с цифрой старшего разряда 3.

Например:

При обработке результатов наблюдений следует пользоваться правилами приближенных вычислений, а округление выполнять по следующим правилам:

Округлять результат измерения следует так, чтобы он оканчивался цифрой того же порядка, что и погрешность. Если значение результата измерения оканчивается нулями, то нуль отбрасывается до того разряда, который соответствует разряду погрешности.

Пример: Погрешность равна 0,0005 м

Поле вычислений получен результат измерения:

2. Если первая из заменяемых нулем или отбрасываемых цифр (слева направо) меньше 5, то остающиеся цифры не изменяются.

Пример:

3. Если первая из заменяемых нулем или отбрасываемых цифр равна 5, а за ней не следует никаких цифр или нулей, то округление производят до ближайшего четного числа, т.е. четную последнюю оставленную цифру или ноль оставляют без изменений, нечетную увеличивают на единицу:

Пример:

4. Если первая из заменяемых нулем или отбрасываемых цифр больше или равна 5, но за ней следует отличная от нуля цифра, то последнюю оставленную цифру увеличивают на единицу.

Пример: =12;

.

При обработке измерений приходится выполнять математические операции над числами. Определение погрешностей этих операций следует проводить по формулам таблицы 6.3.

Таблица 6.3

Формулы для вычисления погрешностей при некоторых операциях над числами

Математическая операция	Абсолютная погрешность	Относительная погрешность
Z=a+b+с	z =a  b  c
Z=a-b
Z=	или
Z =
Z = an
Z =
Z=	при
Z=		при

Округление результатов арифметических операций над приближенными числами следует проводить по следующим правилам.

1.При сложении или вычитании в результате вычислений младший сохраняемый десятичный разряд должен быть тот, который соответствует наименее точному из числе, участвующих в математической операции.

Пример 1.1. Z= a + b + c; a =5,831; b =2,42; с =6,1763; Δ_а =±0,001; Δ_b =±0,03; Δ_с=0,0004.

Z=5,8310+2,4200+6,1763=14,4273≈14,43 ± Δ_Z; Δ_Z=±(0,001+0,003+0,0005)= ±0,0314 ≈ ±0,03. Таким образом, Z ≈ 14,43±0,03 или 14,40≤14,43≤14,46.

Примечание. Для следующих примеров значения a, b, с, Δ_а, Δ_b и Δ_с берутся из примера 1.1.

Пример 1.2. Z= a – b =5,831-2,42=3,411≈3,41±0,03 или 3,38≤3,41≤3,44.

2. При умножении и делении в результате вычислений следует сохранять столько значащих цифр, сколько их имеет число с наименьшим количеством значащих цифр.

Пример 2.1. Z= a х b х c = 5,831 х 2,42 х 6,1763 = 87,153892826 ≈ 87,16 ± Δ_Z.

Δ_Z= ± (2,42 х 6,1763 х 0,001 + 5,831 х 6,1763 х 0,03 + 5,831 х 2,42 х 0,0004) = ± (0,014946646 + 1,080420159 + 0,005644408) = ±1,101011213 ≈ ±1,1.

Т.о., Z ≈ 87,16 ± 1,1 или 86,06 ≤ 87,16 ≤ 88,26.

Пример 2.2. Z = 5,831/2,42 = 2,40950413223 ≈ 2,41 ± Δ_Z = 2,41 ± 0,03 или

2,38 ≤ 2,41 ≤ 2,44.

3. При возведении в квадрат и куб в конечном результате следует сохранять столько значащих цифр, сколько их имеет приближенное значение возводимого в степень числа.

Пример 3.1. Z = 5,831³ = 198,257271191 ±Δ_Z ≈ 198,257 ±Δ_Z. Δ_Z= 3 х 5,831² 0,001=3 х 1156,038114721 х 0,001 = 3,468114444944163 ≈ 3. Т.о., Z ≈ 198,257 ±3 или 195,257≤198,257≤201,257.

4. При извлечении квадратного и кубического корней в результате следует оставить столько значащих цифр, сколько их имеет приближенное значение подкоренного числа.

Пример 4.1. Z = ≈ 1,7999 ±Δ_Z ≈ 1,800 ±Δ_Z. Δ_Z=±( х 5,831² х 0,001) ≈ ±(17,00028 х 0,001) ≈ ±0,01700028 ≈ 0,017. Т.о., Z ≈ 1,800±0,017 или 1,783 ≤ 1,8 ≤ 1,817.

5. При вычислениях по каким-либо формулам следует сохранять на одну цифру больше, чем указано в п.п. 1-4. В окончательном результате эта «запасная» цифра отбрасывается.

6. Если какое-нибудь приближенное число имеет больше десятичных знаков (при сложении и вычитании) или больше значащих цифр (при умножении, делении, возведении в степень, извлечении корня), чем другие, то его следует предварительно округлять, сохраняя лишь одну «лишнюю» цифру.

Числовые значения показателей точности должны содержать не боле двух значащих цифр.

Контрольные вопросы

1.Сколько значащих цифр допускается приводить в погрешности результатов измерений?

2.Каковы правила округления результатов наблюдений?

3. Каковы правила округления результатов расчетов?

3. Как определить погрешность суммы нескольких чисел?

4. Как определить погрешность разности двух чисел?

5. Как определить погрешность произведения трех чисел?