
- •Часть 3. Электричество
- •Электричество Литература
- •§1. Введение
- •Глава 1. Электростатика §2. Законы электростатики
- •§3 Электрическое поле в вакууме. Напряженность и потенциал
- •§4 Электростатическая теория Гаусса
- •§5 Проводники в электрическом поле.
- •§6 Диэлектрики в электрическом поле
- •§7. Энергия электрического поля. Конденсаторы.
- •§8. Законы постоянного тока
- •§9. Ток в металлах.
- •§10. Ток в электролитах
- •§11. Ток в газах.
- •Глава 3. Магнитное поле §12. Магнитное взаимодействие электрических токов
- •§13. Вычисление магнитных полей
- •§ 14. Действие магнитного поля на токи и движущиеся заряды
- •§15. Эффекты, возникающие при движении заряженных частиц в магнитном поле
- •§16. Электромагнитная индукция
- •§17. Поле в магнетиках. Диамагнетизм
- •§18. Пара - и ферромагнетики
- •§19. Уравнения Максвелла
- •Глава 4. Электромагнитные колебания и волны §20. Переменный ток
- •§21. Электрические колебания в колебательном контуре. Колебательные системы.
- •§22. Электромагнитные волны
- •Глава 5. Электрические явления в атмосфере §23. Электричество атмосферы
- •Оглавление
§21. Электрические колебания в колебательном контуре. Колебательные системы.
1. Свободные затухающие колебания. Колебательным контуром называется цепь, содержащая ёмкость С и индуктивность L. Реальный контур всегда имеет некоторое активное (омическое) сопротивление R (рис.150).
Если зарядить конденсатор, а затем замкнуть ключ Кл, то конденсатор будет разряжаться через катушку L, в цепи контура пойдёт ток i = dqdt, где q – заряд на конденсаторе. Чтобы определить зависимость тока от времени (или заряда на обкладках конденсатора), полагаем цепь квазистационарной и составим 2-е правило Кирхгофа для контура: iR = UC + E. Здесь UC = qC – напряжение на обкладках конденсатора, E ЭДС индукция в катушке. При обходе по часовой стрелке на рис.150 получаем:
![]()
 ,
или
,
или
![]() .
(21.1)
.
(21.1)
Знак “минус”
перед напряжением на конденсаторе
qC
ставится потому, что ход потенциала на
конденсаторе при обходе по контуру
противоположен ходу потенциала на
резисторе. Обозначив
RL = 2,
1CL = ![]() ,
а в производных перейдя к точкам,
получаем:
,
а в производных перейдя к точкам,
получаем:
![]() .
(21.2)
.
(21.2)
Это дифференциальное уравнение затухающих колебаний. Вид его решения зависит от соотношения между коэффициентами n и 0. Если 0 > 2n, колебания периодические затухающие, если 0 < 2n, то колебания апериодические.
а .
Периодические затухающие колебания.
Будем полагать, что затухание очень
слабое, так что 0 >> 2n.
Уравнение (21.2) такое же, как уравнение
затухающих колебаний материальной
точки. Его подробное решение см.[2],
§124, с.с.553-556. Опустив выкладки, запишем
приближённое решение уравнения 21.2 для
заряда, тока и напряжения.
.
Периодические затухающие колебания.
Будем полагать, что затухание очень
слабое, так что 0 >> 2n.
Уравнение (21.2) такое же, как уравнение
затухающих колебаний материальной
точки. Его подробное решение см.[2],
§124, с.с.553-556. Опустив выкладки, запишем
приближённое решение уравнения 21.2 для
заряда, тока и напряжения.
q = q0e-ntcost, (21.3)
i = q0 e-ntcos(t + /2), (21.4)
![]() . Здесь
. Здесь
![]() .
(21.5)
.
(21.5)
Графики q(t),
i(t)
и uC(t)
показаны на рис.151. При
малых затуханиях период колебаний в
контуре определяется формулой Томсона,
![]() . (21.6)
. (21.6)
Декремент затухания
![]() .
(21.7)
.
(21.7)
Логарифмический декремент затухания
![]() .
(21.8)
.
(21.8)
Величина
![]() волновое сопротивление
контура,
волновое сопротивление
контура,
![]() добротность.
(21.9)
добротность.
(21.9)
У колебательных контуров среднего качества Q 20 100.
В идеальном контуре, в котором
отсутствует затухание, R = 0,
колебания должны продолжаться бесконечно
долго. При этом максимальная энергия
конденсатора
![]() ,
а максимальная энергия поля катушки
составляет
,
а максимальная энергия поля катушки
составляет
![]() .
Когда конденсатор максимально заряжен,
i = 0,
.
Когда конденсатор максимально заряжен,
i = 0,
![]() ,
вся энергия колебаний заключена в
электрическом поле. Когда конденсатор
разряжен, u = 0,
а ток максимален. Вся энергия контура
заключена в магнитном поле катушки.
Средние и максимальные энергии
электрического и магнитного полей
одинаковы,
,
вся энергия колебаний заключена в
электрическом поле. Когда конденсатор
разряжен, u = 0,
а ток максимален. Вся энергия контура
заключена в магнитном поле катушки.
Средние и максимальные энергии
электрического и магнитного полей
одинаковы,
![]() .
Однако колебания в любом реальном
контуре даже из сверхпроводящих
материалов обязательно затухают. Это
происходит потому, что контур с переменным
током излучает электромагнитные волны,
которые уносят запасённую в нём энергию.
В дифференциальном уравнении эти потери
не учтены.
.
Однако колебания в любом реальном
контуре даже из сверхпроводящих
материалов обязательно затухают. Это
происходит потому, что контур с переменным
током излучает электромагнитные волны,
которые уносят запасённую в нём энергию.
В дифференциальном уравнении эти потери
не учтены.
б .
Апериодические колебания происходят
при n > 0.
Если n >> 0
и в цепи контура нет внешних ЭДС, то
колебания представляют собой простой
разряд конденсатора на выскоомный
резистор. Заряд, напряжение на конденсаторе
и ток изменяются в этом случае по
экспоненциальному закону (рис.152):
.
Апериодические колебания происходят
при n > 0.
Если n >> 0
и в цепи контура нет внешних ЭДС, то
колебания представляют собой простой
разряд конденсатора на выскоомный
резистор. Заряд, напряжение на конденсаторе
и ток изменяются в этом случае по
экспоненциальному закону (рис.152):
![]() (21.10)
(21.10)
Здесь
![]() .
Из равенства n = 0
находим критическое сопротивление
контура, разделяющее периодические
колебания от апериодических. n = 0,
.
Из равенства n = 0
находим критическое сопротивление
контура, разделяющее периодические
колебания от апериодических. n = 0, ![]() ,
,
![]() .
(21.11)
.
(21.11)
Если сопротивление резистора R больше удвоенного волнового сопротивления периодические колебания в контуре не возникают.
2 .
Вынужденные колебания возникают
тогда, когда в контуре действует внешняя
переменная ЭДС (рис.153). В отличие от
подобного случая в цепи переменного
тока, рассмотренного в §20, п.7, здесь
полагаем, что диапазон частот, генерируемых
внешним источником, много шире, а
внутреннее сопротивление источника
внешней ЭДС много больше.
.
Вынужденные колебания возникают
тогда, когда в контуре действует внешняя
переменная ЭДС (рис.153). В отличие от
подобного случая в цепи переменного
тока, рассмотренного в §20, п.7, здесь
полагаем, что диапазон частот, генерируемых
внешним источником, много шире, а
внутреннее сопротивление источника
внешней ЭДС много больше.
Если в контуре действует периодическая
ЭДС E =Eacost,
то уравнение колебаний электрического
заряда на обкладках конденсатора
принимает вид:
![]() .
(21.12)
.
(21.12)
Здесь те же обозначения: 2n = RL,
![]() .
.
Решение этого уравнения состоит из двух членов и при n << 0 имеет вид: q = q0entcost + Bcos(t ). (21.13)
Первый член описывает собственные затухающие колебания в контуре, рассмотренные в предыдущем пункте. Спустя некоторое время (не более нескольких секунд). Эти колебания практически исчезают. Остаётся лишь вторая часть, описывающие вынужденные колебания q = Bcos(t ). (21.14)
Здесь B – амплитуда
вынужденных колебаний,
- угол сдвига по фазе по отношению
к собственным колебаниям.
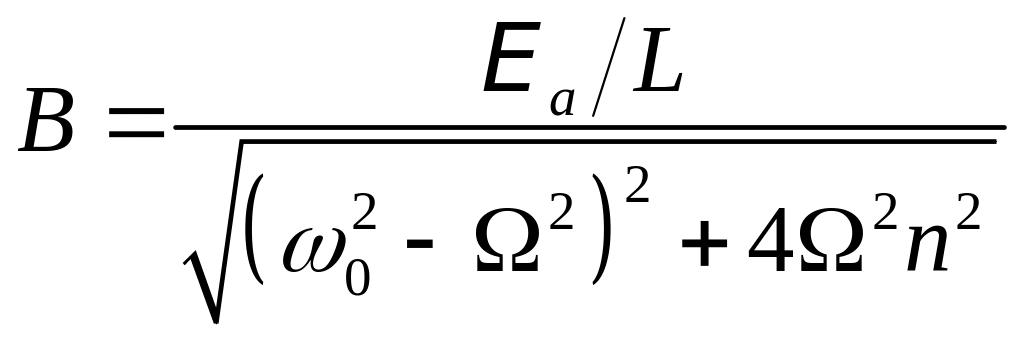 ,
, ![]() .
(21.15)
.
(21.15)
Дифференцируя (21.14) по времени, получаем ток в контуре.
i =![]() = Bsin(t ) = Bcos(t + 2).
(21.16)
= Bsin(t ) = Bcos(t + 2).
(21.16)
Величина В = ia
есть амплитудный ток. Он зависит от
соотношения частот 0
и . Если частота
изменения внешней ЭДС приближается к
частоте 0
собственных затухающих колебаний, то
ток в контуре возрастает до некоторого
максимального значения, называемого
резонансным.
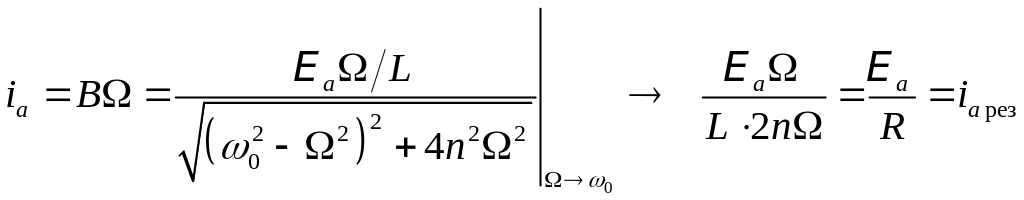 .
(21.17)
.
(21.17)
Р ассмотренная
ситуация соответствует резонансу
напряжений в цепи переменного тока, а
формула амплитудного тока (21.17) в общем
виде соответствует закону Ома для цепи
переменного тока. Так как
,
n = R / 2L,
то
ассмотренная
ситуация соответствует резонансу
напряжений в цепи переменного тока, а
формула амплитудного тока (21.17) в общем
виде соответствует закону Ома для цепи
переменного тока. Так как
,
n = R / 2L,
то
 .
(21.18)
.
(21.18)
На рис.154 показаны амплитудные резонансные кривые – графики зависимости амплитудного тока ia от частоты внешней ЭДС. Чем больше добротность контура Q = R, тем уже его резонансная кривая, тем выше его избирательность (селективность). Поэтому с увеличением добротности Q ширина вынуждающих частот ( 0), при которых в контуре раскачиваются значительные токи, становится уже. Этот интервал частот, близких к 0, называется полосой пропускания контура. Сюда входят частоты от 1 до 2, где 1 и 2 – частоты, при которых энергия колебания в 2 раза меньше энергии колебаний в резонансе. Можно показать, что = 2n.
Действительно, энергия амплитудного тока в резонансе
![]() .
(21.19)
.
(21.19)
Если при некоторой частоте , энергия амплитудного тока в 2 раза меньше, то есть
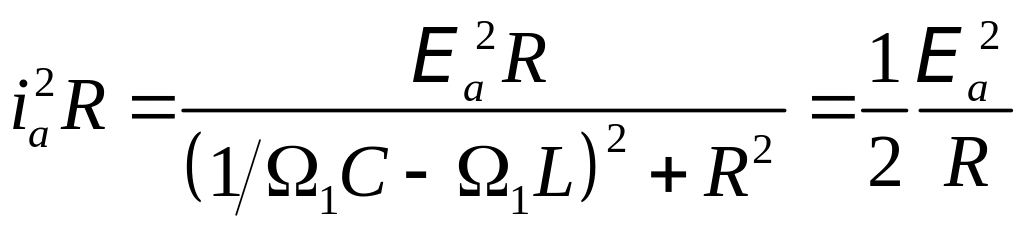 ,
(21.20)
,
(21.20)
то отсюда найдётся 1. Чтобы равенство (21.20) выполнялось, должно быть
![]() , или
, или ![]() .
(21.21)
.
(21.21)
Решение этого квадратного уравнения:
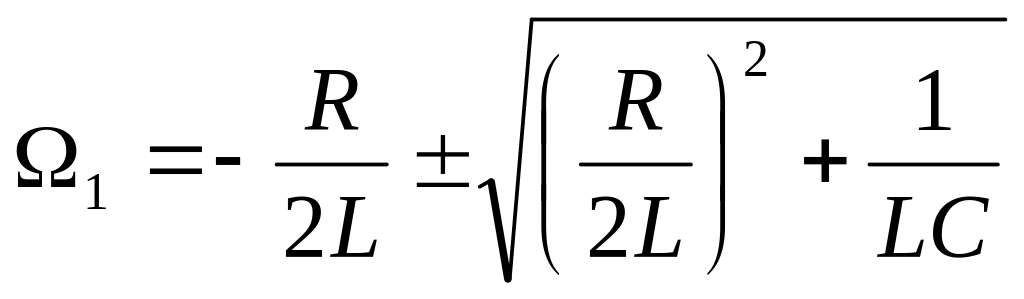 .
(21.22)
.
(21.22)
По условию, принятому вначале, затухание очень слабое, (R2L)2 << (1LC). Поэтому первым слагаемым под корнем можно пренебречь. 1 = n 0. (21.23)
Значение 1 = n 0 < 0 и не имеет физического смысла. Остаётся 1 = 0 n. (21.24)
Полуширина полосы пропускания
![]() ,
(21.25)
,
(21.25)
а ширина полосы пропускания в 2 раза
больше
![]() .
(21.26)
.
(21.26)
3. Искровой колебательный контур. Реализовать гармоническую ЭДС частотой в тысячи и миллионы герц путём вращения рамки в магнитном поле практически невозможно. Поэтому для возбуждения в колебательном контуре незатухающих колебаний высокой частоты используются другие способы.
И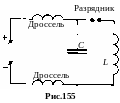 сторически
первым шагом в этом направлении следует
рассматривать искровой колебательный
контур, которой изобрёл в 1888 г. немецкий
физик Генрих Герц (рис.155).
сторически
первым шагом в этом направлении следует
рассматривать искровой колебательный
контур, которой изобрёл в 1888 г. немецкий
физик Генрих Герц (рис.155).
П осле
включения источника постоянного
напряжения конденсатор через дроссельные
катушки заряжается, и напряжение между
его обкладками увеличивается. Когда
оно достигает значения напряжения
пробоя, через разрядник проскакивает
искра, замыкающая колебательный контур,
и в контуре возникает цуг затухающих
колебаний. Он обрывается, когда напряжение
на искровом разряднике упадёт до
напряжения гашения искры. Затем
конденсатор снова заряжается, и всё
повторяется в той же последовательности
(рис.156).
осле
включения источника постоянного
напряжения конденсатор через дроссельные
катушки заряжается, и напряжение между
его обкладками увеличивается. Когда
оно достигает значения напряжения
пробоя, через разрядник проскакивает
искра, замыкающая колебательный контур,
и в контуре возникает цуг затухающих
колебаний. Он обрывается, когда напряжение
на искровом разряднике упадёт до
напряжения гашения искры. Затем
конденсатор снова заряжается, и всё
повторяется в той же последовательности
(рис.156).
Колебания, получаемые Герцем, имели частоту порядка 5108 Гц, что соответствует длине излучаемых его вибратором электромагнитных волн 60 см.
В 1891 г. серб Никола Тесла изобрёл высокочастотный трансформатор, т.н. трансформатор Тесла, позволяющий получать колебания с частотой до 105 Гц напряжением до 7106 В. В качестве первичного контура в трансформаторе Тесла используется искровой генератор высокочастотных колебаний. В начале развития радиотехники трансформатор Тесла применялся на радиостанциях в качестве источника ВЧ колебаний, в настоящее время – в учебной практике в демонстрационных экспериментах.
Искровой колебательный контур представляет собой автоколебательную систему. Один из главных недостатков его в том, что энергия вводится слишком редко, раз в течение одного цуга, точнее – между цугами. Поэтому трудно обеспечить стабильность амплитуды ВЧ колебаний.
Наибольшее распространение получили автоколебательные генераторы незатухающих колебаний на основе ламповых триодов и, позднее, полупроводниковых транзисторов.
4 .
Генератор ВЧ колебаний на ламповом
триоде. В 1907 г. американец Ли де Форест
изобретает важнейший радиотехнический
элемент первой половины XX
века – электронную лампу с тремя
электродами – триод. Анод и катод
в триоде разделены между собой третьим
электродом – сеткой.
.
Генератор ВЧ колебаний на ламповом
триоде. В 1907 г. американец Ли де Форест
изобретает важнейший радиотехнический
элемент первой половины XX
века – электронную лампу с тремя
электродами – триод. Анод и катод
в триоде разделены между собой третьим
электродом – сеткой.
На рис.157 показана схема простейшего лампового генератора на триоде, позволяющего получать незатухающие ВЧ колебания.
Вследствие тепловых флуктуаций электронов контуре C–L1 самопроизвольно возникают слабые колебания. Но изменение напряжения на обкладках конденсатора С вызывает изменение потенциала сетки S триода. При положительном потенциале верхней (по рисунку) пластины конденсатора триод открывается, в анодной цепи течёт ток, который через индуктивную связь между катушками L1 и L2 усиливает ток в контуре.
Когда конденсатор перезарядится в обратном направлении, лампа заперта, через катушку L2 тока нет. Затем весь процесс повторяется. Таким образом, ток в анодной цепи течёт лишь в те моменты времени, когда лампа открыта, и когда магнитное поле катушки L2 подпитывает ток в контуре.
Управление электронной лампой с помощью цепи обратной связи может осуществляться разными способами. Наряду с рассмотренной индуктивной связью часто применяется также ёмкостная и автотрансформаторная обратная связь.
5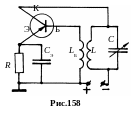 .
Генератор на транзисторе типа р – n – p
c индуктивной обратной связью
(рис.158). При отсутствии колебаний ток
эмиттера очень мал, а напряжение на
эмиттерном p – n
переходе близко к нулю, поскольку
почти всё падение напряжения приходится
на обратный n – p
переход. Если в колебательном контуре
возникли флуктуационные колебания, то
в катушке LБ
индуцируется периодическая ЭДС, которая
создаёт пульсирующий ток в цепи
эмиттер – база. Это приводит к
увеличению коллекторного тока, который,
проходя по катушке L,
увеличивает амплитуду колебаний тока
в контуре.
.
Генератор на транзисторе типа р – n – p
c индуктивной обратной связью
(рис.158). При отсутствии колебаний ток
эмиттера очень мал, а напряжение на
эмиттерном p – n
переходе близко к нулю, поскольку
почти всё падение напряжения приходится
на обратный n – p
переход. Если в колебательном контуре
возникли флуктуационные колебания, то
в катушке LБ
индуцируется периодическая ЭДС, которая
создаёт пульсирующий ток в цепи
эмиттер – база. Это приводит к
увеличению коллекторного тока, который,
проходя по катушке L,
увеличивает амплитуду колебаний тока
в контуре.
Когда конденсатор С разряжается в обратном направлении, ЭДС в катушке LБ запирает эмиттерный ток, что приводит к уменьшению коллекторного тока. Поэтому обратная перезарядка конденсатора происходит беспрепятственно при минимальном токе коллектора.
Модификаций схем генераторов на транзисторах очень много.
6. Токи высокой частоты, ТВЧ. С помощью генераторов электрических колебаний можно вырабатывать почти синусоидальные переменные токи частотой в тысячи и миллионы герц. Благодаря вытеснению быстропеременных токов к периферии проводника вследствие скин-эффекта (см. след. параграф), оказывается возможным с помощью ТВЧ закаливать поверхность стальных деталей, не уменьшая их пластичности в глубине. Использование токов частотой в сотни и тысячи герц эффективно при индукционном нагреве металлов в плавильных индукционных электропечах, поскольку вихревые токи Фуки увеличиваются с ростом частоты электромагнитного поля.
Т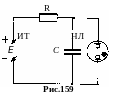 ВЧ
широко используются при высокочастотной
сварке и в многоканальной телефонной
связи.
ВЧ
широко используются при высокочастотной
сварке и в многоканальной телефонной
связи.
7. Релаксационный генератор. Наряду с генераторами почти синусоидальных колебаний, рассмотренными выше, в практике широко используются устройства, создающие периодические, но далеко не гармонические колебания, напр., пилообразные, П – образные и др. Рассмотрим генератор пилообразных колебаний на неоновой лампе (рис.159).
К онденсатор
С, параллельно которому присоединена
неоновая лампа НЛ, через резистор R
с большим сопротивлением заряжается
от источника постоянного тока ИТ, в
результате напряжение на обкладках
повышается. Когда напряжение на
конденсаторе С достигает напряжения
зажигания Uз,
в лампе возникает газовый разряд, и
конденсатор начинает быстро разряжаться.
Когда напряжение на конденсаторе подает
до напряжения гашения в
лампе Uг,
разряд в лампе обрывается, и конденсатор
вновь начинает заряжаться. Возникают
так называемые релаксационные колебания
(рис.160).
онденсатор
С, параллельно которому присоединена
неоновая лампа НЛ, через резистор R
с большим сопротивлением заряжается
от источника постоянного тока ИТ, в
результате напряжение на обкладках
повышается. Когда напряжение на
конденсаторе С достигает напряжения
зажигания Uз,
в лампе возникает газовый разряд, и
конденсатор начинает быстро разряжаться.
Когда напряжение на конденсаторе подает
до напряжения гашения в
лампе Uг,
разряд в лампе обрывается, и конденсатор
вновь начинает заряжаться. Возникают
так называемые релаксационные колебания
(рис.160).
Найдём период колебаний. В процессе
заряда конденсатора 2-е правило Кирхгофа
имеет вид iR + u = E,
или
![]() .
(21.27)
.
(21.27)
Здесь u –
напряжение на конденсаторе, E
ЭДС
источника тока. Перейдём к переменной
u. Так как q = Cu,
то
![]() ,
и
,
и
![]() .
(21.28)
.
(21.28)
Если обозначить u E = U,
то
![]() и получаем уравнение с разделяющимися
переменными:
и получаем уравнение с разделяющимися
переменными:
![]() .
Отсюда
.
Отсюда
![]() ,
,
![]() .
(21.29, 30)
.
(21.29, 30)
Постоянную интегрирования U0 найдём из начального условия: напряжение на конденсаторе в начале заряда равно нулю, u = 0. Тогда U0 = U E (t = 0) = 0 E = E, U = E exp(tCR). Вернувшись к прежней переменной, получаем:
u = U +E = E (1 – exp(tCR)). (21.31)
Если пренебречь временем разряда
конденсатора по сравнению с его временем
заряда, то период колебаний можно найти
как время заряда конденсатора от uГ
до uЗ.
Пусть заряда до напряжения uГ
достигается к моменту времени t1,
а заряд напряжения uЗ
– к моменту времени t2.
Так как uГ = E
(1 – exp(t1CR)),
uЗ= E
(1 – exp(t2CR),
то выразив из этих уравнений моменты
t1
и t2
и найдя их разность, получаем период
релаксационных колебаний.
![]() .
(21.32)
.
(21.32)
