[Править] Определение

Если приготовлены несколько идентичных копий системы в данном состоянии, то измеренные значения координаты и импульса будут подчиняться определенному распределению вероятности— это фундаментальный постулат квантовой механики. Измеряя величинустандартного отклоненияΔx координаты и стандартного отклонения Δp импульса, мы найдем что:

,

где «» являетсяпостоянной Планка(h) поделенной на 2π. (В некоторых рассмотрениях «неопределенность» переменной определяется как наименьшая ширина диапазона, который содержит 50 % значений, что, в случаенормального распредения переменных, приводит для произведения неопределенностей к большей нижней границеh/2π.) Отметьте, что это неравенство даёт несколько возможностей — состояние может быть таким, чтоxможет быть измерен с высокой точностью, но тогдаpбудет известен только приблизительно, или наоборотpможет быть определен точно, в то время какx— нет. Во всех же других состояниях, иxиpмогут быть измерены с «разумной» (но не произвольно высокой) точностью.

В повседневной жизни мы обычно не наблюдаем неопределенность потому, что значение hчрезвычайно мало.

23, Уравне́ние Шрёдингерав квантовой физике — уравнение, связывающее пространственное распределение амплитуды вероятности с энергией частицы. ПредложеноавстрийскимфизикомЭрвином Шрёдингеромв1925в качестве окончательного объясненияатомной структурыс помощью представлений оволновой функции. Играет вквантовой механикетакую же важную роль, как уравнениевторого закона Ньютонавклассической механике. Его можно назвать уравнением движенияквантовой частицыВквантовой физикеизначально вводится представление овероятностномповедении частицы путем задания некоторой функции, называемой волновой и характеризующей вероятность местонахождения частицы (см.Волновая функция). Затем выводится уравнение для этой функции.

Отказавшись от описания движения частицы с помощью траекторий, получаемых из законов Ньютона, и определив вместо этого волновую функцию (), необходимо ввести в рассмотрение уравнение, эквивалентное законам Ньютона и дающее рецепт для нахождения в частных физических задачах. Искомым уравнением будет уравнение Шрёдингера.

Пусть волновая функция задана в N-мерном пространстве, тогда в каждой точке с координатами , в определенный момент времениtона будет иметь вид. В таком случае уравнение Шрёдингера запишется в виде:

где ,—постоянная Планка;—массачастицы,— внешняя по отношению к частицепотенциальная энергияв точке,—оператор Лапласа(илилапласиан), эквивалентен квадратуоператора набла, и в частном случаедекартовых координат, имеет вид:

[Править] Случай трёхмерного пространства

В трёхмерномслучае неизвестные являются функциями трех координат ивдекартовой системе координатзаменяется выражением

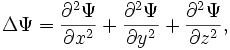
тогда уравнение Шрёдингера примет вид:

где ,—постоянная Планка;—массачастицы,—потенциальная энергияв точке

[Править] Стационарное уравнение Шрёдингера

Форма уравнения Шрёдингера показывает, что относительно времени его решение должно быть простым, поскольку время входит в это уравнение лишь через первую производную в правой части. Действительно, частное решение для специального случая, когда не является функцией времени, можно записать в виде:

где функция должна удовлетворять уравнению:

которое получается из уравнения Шрёдингера (1)при подстановке в него указанной выше формулы для(2). Заметим, что это уравнение вообще не содержит времени; в связи с этим оно называетсястационарным уравнением Шрёдингера (уравнение Шрёдингера, не содержащее времени).

Выражениe (2)является лишьчастным решениемзависящего от времени уравнения Шрёдингера(1), общее решение представляет собойлинейную комбинациювсех частных решений вида(2). Зависимость функцииот времени проста, но зависимость ее от координаты не всегда имеетэлементарный вид, так как уравнение(3)при одном выборе вида потенциальной функциисовершенно отличается от того же уравнения при другом выборе этой функции. В действительности уравнение(3)может быть решено аналитически лишь для небольшого числа частных типов функции.

Важное значение имеет интерпретациявеличиныв уравнении(2). Она производится следующим путём: временна́я зависимость функциив уравнении(2)имеетэкспоненциальныйхарактер, причём коэффициент прив показателе экспоненты выбран так, что правая часть уравнения(3)содержит просто постоянный множитель. В левой же части уравнения(3)функцияумножаетсяна потенциальную энергию. Следовательно, из соображенийразмерностивытекает, что величинадолжна иметь размерностьэнергии. Единственной величиной с размерностью энергии, которая постоянна вмеханике, является полная (сохраняющаяся) энергия системы; таким образом, можно предполагать, чтопредставляет собойполную энергию. Согласно физической интерпретации уравнения Шрёдингера,действительно является полной энергией частицы при движении, описываемом функцией.