Брянский колледж экономики, статистики и информатики

УТВЕРЖДАЮ:

Заместитель директора по УМР

____________Т.Н. Кузина

«____» _______________

ИНСТРУКЦИЯ К ЛАБОРАТОРНОЙ РАБОТЕ №8

«Численное решение обыкновенных дифференциальных уравнений»

По предмету «Численные методы» для студентов специальности 230105

«Программное обеспечение ВТ и автоматизированных систем»

Инструкция составлена преподавателем Ноздрачевой Н.Л.

Согласовано на заседании цикловой комиссии математики, информатики и программирования

Протокол заседания № ___ от ____________ 200 г.

Председатель комиссии _________ Н.К. Минина

Брянск

Содержание

1. Цель работы.

2. Приборы и оборудование.

3. Общие теоретические сведения.

4. Задание.

5. Порядок выполнения работы.

6. Отчет о выполненной работе.

7. Контрольные вопросы.

8. Литература.

1. Цель работы:

1. Закрепить знание основных алгоритмов решения обыкновенных дифференциальных уравнений.

2. Разработать программу решения обыкновенных дифференциальных уравнений методами:

• методом Эйлера;

• методом Эйлера с двойным счетом;

• методом Эйлера – Коши с двойным счетом;

• методом Рунге – Кутта.

3. Найти решения обыкновенных дифференциальных уравнений различными методами.

4. Сравнить результаты, полученные различными методами.

5. Закрепить умения и навыки работы с программой и основными компонентами в среде программирования Delphi.

2. Приборы и оборудование:

1. ПК, система программирования Delphi.

3. Общие теоретические сведения

3.1. Постановка задачи

Обыкновенным дифференциальным уравнением называется уравнение вида Решить такое уравнение численным методом это значит для заданной последовательности аргументов и числа , не определяя функции найти такие значения что где и

Таким образом, численные методы позволяют вместо нахождения функции получить таблицу значений этой функции для заданной последовательности аргумента и начального условия

3.2. Метод Эйлера

Пусть дано дифференциальное уравнение с начальным условием Требуется найти решения данного уравнения на

Разобьём отрезок на n равных частей. Получили последовательность чисел . Шаг или . Проинтегрируем данное дифференциальное уравнение по . Получим:

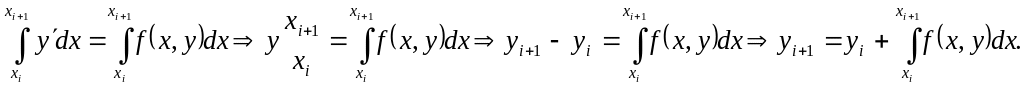
Т

ак как отрезки достаточно малы, то подынтегральную функцию можно принять постоянной .Значит: .

Отсюда получаем формулу Эйлера:

Таким образом, если известна функция , начальное условие , шаг h и отрезок , то по этой формуле можно найти все решения дифференциального уравнения на данном отрезке.

Метод Эйлера обладает малой точностью, к тому же погрешность каждого нового шага возрастает. Поэтому он применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу этого метода, являются исходными для ниже следующих методов.

3.3. Метод Эйлера – Коши (уточненный метод Эйлера)

С

уществуют различные уточнения метода Эйлера, повышающие его точность. Один из таких методов это метод Эйлера – Коши. В этом методе сначала вычисляется вспомогательное значение по формуле:

А

затем вычисляется само значение по формуле с использованием ранее найденного значения :

3.4. Метод Рунге – Кутта

Это один из методов повышенной точности.

3.5 Определение погрешности найденных решений

Для определения погрешности с которой находятся решения дифференциального уравнения на данном отрезке используется способ двойного счета:

1. Находим значения для всех x_i из отрезка с заданным шагом h.

2. Находим значения для всех x_i из отрезка с шагом h/2.

3. Погрешность каждого найденного определяется по формуле

1. Метод Эйлера: ;

2. Метод Эйлера – Коши: ;

3. Метод Рунге – Кутта: