20. Определение нормального оператора. Связь унитарного и нормального оператора.

Начало формы

НОРМАЛЬНЫЙ ОПЕРАТОР- замкнутый линейный оператор А, определенный на плотном в гильбертовом пространстве H линейном многообразии D_A, такой, что , где - оператор, сопряженный с А. Если А- Н. о., то Обратно, выполнение этих условий обеспечивает нормальность А. Если А-Н. о., то: также нормален; - Н. о. при любых нормален в случае, когда этот оператор существует, если где В- ограниченный линейный оператор, то также

Как унитарные, так и самосопряженные операторы в унитарном пространстве являются частным случаем нормальных операторов.

21. Кольцо. Изоморфизм колец

В абстрактной алгебре кольцо́ — это один из наиболее часто встречающихся видов алгебраической структуры.

Кольцо — это множество R, на котором заданы две бинарные операции: + и × (называемые сложение и умножение)

кольцо — это универсальная алгебра , такая что алгебра  — абелева группа, и операция дистрибутивна слева и справа относительно

Теоремы об изоморфизме в алгебре — ряд теорем, связывающих понятия фактора, гомоморфизма и вложенного объекта. Утверждением теорем является изоморфизм некоторой пары групп, колец, модулей, линейных пространств, алгебр Ли или прочих алгебраических структур (в зависимости от области применения).

В данной области понятие нормальной подгруппы заменяется на понятие идеала кольца.

Первая теорема

Пусть гомоморфизм колец, тогда:

1. Ядро φ — идеал в R;

2. Образ φ — подкольцо в S;

3. Образ φ изоморфен факторкольцу R / ker φ.

В частности, если гомоморфизм φ сюръективен (т.е. является эпиморфизмом), то кольцо S изоморфно факторкольцу R / ker φ.

Вторая теорема

Пусть R — кольцо, S — подкольцо в R, I — идеал в R, тогда:

1. Сумма S + I — подкольцо в R;

2. Пересечение S ∩ I — идеал в S;

3. Факторкольца (S + I) / I и S / (S ∩ I) изоморфны.

Третья теорема

Пусть R — кольцо, A и B — идеалы в R такие, что B ⊆ A, тогда:

1. A / B — идеал в R / B;

2. Факторкольцо факторколец (R / B) / (A / B) изоморфно факторкольцу R / A.

22. Поле. Изоморфизм полей.

По́лем называется множество F с двумя бинарными операциями (аддитивная операция, или сложение) и (мультипликативная операция, или умножение), если оно (вместе с этими операциями) образует коммутативное ассоциативное кольцо c единицей , все ненулевые элементы которого обратимы.

Иными словами, множество F с двумя бинарными операциями (сложение) и (умножение) называется полем, если оно образует коммутативную группу по сложению, все его ненулевые элементы образуют коммутативную группу по умножению, и выполняется свойство дистрибутивности.

23. Группа. Свойства групп.

Гру́ппа  — непустое множество с определённой на нём бинарной операцией, удовлетворяющей указанным ниже аксиомам.

Непустое множество с заданной на нём бинарной операцией называется группой , если выполнены следующие аксиомы:

1. ассоциативность: ;

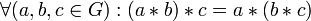2. наличие нейтрального элемента: ;

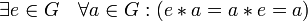3. наличие обратного элемента:

Простейшие свойства

• Обратный к данному элемент всегда определяется однозначно.

• (a⁻¹)⁻¹ = a, a^maⁿ = a^m+n, (a^m)ⁿ = a^mn.

• (ab)⁻¹ = b⁻¹a⁻¹.

• Верны законы сокращения:

,

.

• Обратный элемент к нейтральному есть сам нейтральный элемент.

• Группа содержит единственное решение x любого уравнения x · c = b или c · x = b; то есть в группе возможны однозначно определённые правое и левое «деление».

• Пересечение двух подгрупп группы G есть подгруппа группы G.

• Теорема Лагранжа: если G — группа конечного порядка g, то порядок g₁ любой её подгруппы G₁ является делителем порядка группы. Из этого следует, что и порядок любого элемента делит порядок группы.

• Для определения числа подгрупп в группе используются теорема Лагранжа и теоремы Силова.