
- •Лекция 1
- •1. Запись чисел в десятичной системе счисления. Теорема о существовании и единственности десятичной записи натурального числа.
- •2. Теорема о сравнении натуральных чисел по их десятичной записи. Образование названий и запись натуральных чисел.
- •3.Сложение чисел в десятичной системе счисления. Алгоритм сложения.
- •4. Вычитание натуральных чисел в десятичной системе счисления.
- •8. Умножение натуральных чисел в десятичной системе счисления.
- •9. Деление натуральных чисел в десятичной системе счисления.
- •10. Позиционные системы счисления, отличные от десятичной.
- •1. Отношение делимости во множестве целых неотрицательных чисел, его основные
- •2. Признаки делимости.
- •3. Нод и нок чисел, их свойства. Пункт 1. Общий делитель и наибольший общий делитель.
- •Пункт 2. Свойства нод.
- •Пункт 3. Взаимнопростые числа.
- •Пункт 4. Наименьшее общее кратное целых чисел.
- •4. Признак делимости на составное число.
- •5. Простые и составные числа. Свойства простых чисел.
- •П.2. Основные свойства простых и составных чисел
- •6. «Решето Эратосфена».
- •7. Основная теорема арифметики.
- •8. Алгоритм Евклида. Алгоритм Евклида и нод двух целых чисел.
3. Нод и нок чисел, их свойства. Пункт 1. Общий делитель и наибольший общий делитель.
Определение
1. Целое
число
называется общим делителем целых чисел
и
,
если
![]() и
и
![]() ,
то есть
,
то есть
![]() .
.
Определение
2. Целое
число
![]() называется наибольшим общим делителем
и
,
если
называется наибольшим общим делителем
и
,
если
-
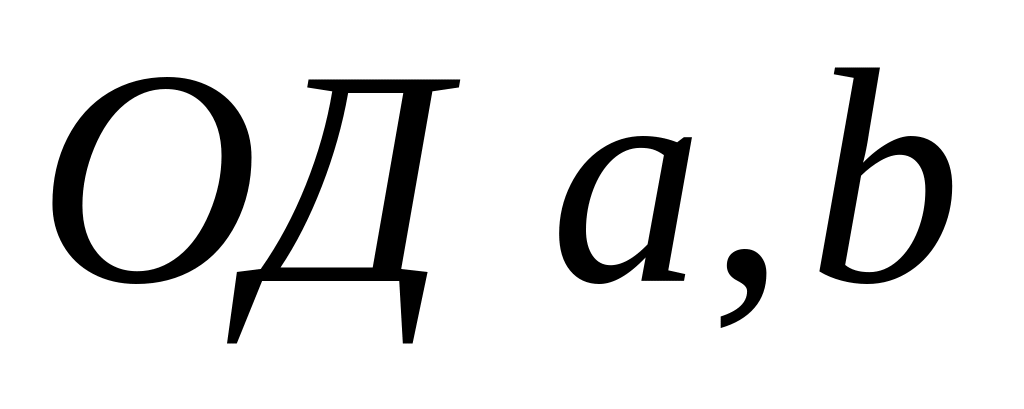 ;
;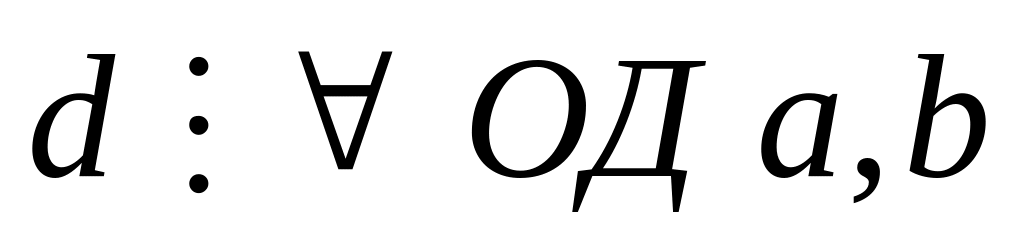 .
.
Предложение 1. НОД двух целых чисел определяется с точностью до знака.
Замечание 1. Далее будем считать, что НОД двух целых чисел есть число положительное.
Предложение
2. Если
,
тогда НОД(![]() )
=
.
)
=
.
Доказательство:
Пусть
.
По свойству 1 ![]() .
Тогда по определению НОД(
)
=
.
.
Тогда по определению НОД(
)
=
.
Предложение
3. Пусть
![]() и
и
![]() ,
тогда НОД(
)=НОД(
,
тогда НОД(
)=НОД(![]() ).
).
Доказательство:
Пусть ![]() .
Тогда
или
.
Тогда
или ![]() ,
,
![]() . Тогда по свойству 5
. Тогда по свойству 5 ![]() .
Так как
и
,
то
.
Так как
и
,
то ![]() .
Следовательно,
.
Следовательно, ![]() .
.
Замечание 2. Определение 1 и определение 2 можно обобщить на случай любого конечного числа целых чисел.
Пункт 2. Свойства нод.
1. Наибольший из общих делителей и , является их наибольшим общим делителем.
2. (О линейном представлении НОД).
Если
![]() ,
тогда
,
тогда
![]() такие, что
такие, что
![]() .
.
Доказательство:
Рассмотрим множество ![]() .
Очевидно, что
.
Очевидно, что ![]() .
Пусть
.
Пусть ![]() и
и ![]() .
Тогда остаток от деления
на
принадлежит
.
Тогда остаток от деления
на
принадлежит ![]() .
Действительно:
.
Действительно: ![]() ,
тогда
,
тогда ![]() .
.
Пусть
![]() - наименьшее положительное число из P.
Тогда а делится на d. В самом деле,
- наименьшее положительное число из P.
Тогда а делится на d. В самом деле, ![]() ,
значит
,
значит ![]() ,
следовательно,
,
следовательно, ![]() .
Аналогичными рассуждениями получается,
что b делится на d, значит d - общий делитель
a и b.
.
Аналогичными рассуждениями получается,
что b делится на d, значит d - общий делитель
a и b.
Далее,
если ![]() ,
то
,
то ![]() .
Если теперь
- общий делитель a и b, то
.
Если теперь
- общий делитель a и b, то ![]() ,
т.е.
,
т.е. ![]() .
Значит
.
Значит ![]() и d - наибольший общий делитель.
и d - наибольший общий делитель.
3.
Если каждое из чисел
и
умножить на
![]() ,
то и их НОД
умножится
на
.
,
то и их НОД
умножится
на
.
4. (О нахождении НОД целых чисел).
Пусть
![]() - целые числа и
- целые числа и
![]() ,
и
,
и
![]() ,
и так далее, и
,
и так далее, и
![]() ,
тогда
,
тогда
![]() .
.
Пункт 3. Взаимнопростые числа.
Определение
1. Целые числа а
и b
называются взаимнопростыми, если
![]() .
.
Определение
2. Числа
![]() называются взаимнопростыми, если
называются взаимнопростыми, если
![]() .
.
Определение 3. Целые числа называются попарно взаимнопростыми, если любая пара этих чисел является взаимнопростой.
Теорема
(Критерий
взаимной простоты).
Целые числа а
и b
являются взаимнопростыми тогда и только
тогда, когда существуют целые числа х
и
у
такие, что
![]() .
.
Доказательство: Необходимость: Пусть и взаимно просты. Тогда по свойству 2 пункта 2 .
Достаточность:
Пусть
и числа
и
не взаимно просты, то есть ![]() .
Тогда
.
Тогда ![]() и
и ![]() .
Следовательно,
.
Следовательно, ![]() x+
x+![]() .
По условию
.
По условию ![]() .
Тогда так как 1 не может делиться на
,
то
.
Тогда так как 1 не может делиться на
,
то ![]() .
Следовательно,
и
взаимно просты.
.
Следовательно,
и
взаимно просты.
Свойства взаимнопростых чисел.
1.Если с взаимнопросто с каждым из целых чисел а и b, то оно взаимопросто с произведением аb.
Следствие:
Если каждое из чисел
![]() взаимнопросто с каждым из
взаимнопросто с каждым из
![]() ,
то каждое из чисел
взаимнопросто с
,
то каждое из чисел
взаимнопросто с
![]() .
.
2.
Если
![]() и
в
и с
взаимнопросты, то
и
в
и с
взаимнопросты, то
![]() .
.
Следствие:
Если а
и b
взаимнопросты и к
- произвольное
натуральное число, то взаимнопростыми
будут и числа
![]() и
и
![]() .
.
3.Если
![]() ,
тогда
,
тогда
![]() .
.
Пункт 4. Наименьшее общее кратное целых чисел.
Определение
1.
![]() Z
называется общим кратным а
и b,
если
Z
называется общим кратным а
и b,
если
![]() и
и
![]() .
.
Определение
2.
![]() Z
называется наименьшим общим кратным а
и b,
если
Z
называется наименьшим общим кратным а
и b,
если
1)
![]() ;
;
2)
![]() .
.
Предложение. НОК двух целых чисел определяется с точностью до знака.
Замечание 1. Далее будем считать, что НОК двух целых чисел есть число положительное.
Теорема.
(О связи НОД
и
НОК двух
натуральных чисел). Пусть
![]() N,
тогда
N,
тогда
![]() .
.
Следствие.
Если
Z,
тогда
![]() .
.
Используя теорему НОД и НОК можно перечислить свойства наименьшего общего кратного:
1º. Наименьшее положительное общее кратное чисел а и b является их НОК.
2º.
Если целые числа а
и b
взаимнопросты, то
![]() .
.
3º.
Если каждое из чисел а
и b
умножить
на число
Z,
то
![]() умножится на m.
умножится на m.
4º. (Нахождение НОК m чисел)
Пусть
![]() Z
и
Z
и
![]() ,
и
,
и
![]() ,
и так далее, и
,
и так далее, и
![]() ,
тогда
,
тогда
![]() .
.
