3. Условия на простое число p
Таблицу составляем по строке.
(p,p+4,p+10,p+12,p+16,p+22,p+24,p+30,p+36,p+40,p+42,p+46,p+52,p+54,p+60,p+64,p+66,
p+70)
У каждого она своя! У всех разные! Не вздумайте списывать друг у друга!
|
0 |
4 |
10 |
12 |
16 |
22 |
24 |
30 |
36 |
40 |
42 |
46 |
52 |
54 |
60 |
64 |
66 |
70 |
3 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
5 |
0 |
4 |
0 |
2 |
1 |
2 |
4 |
0 |
1 |
0 |
2 |
1 |
2 |
4 |
0 |
4 |
1 |
0 |
7 |
0 |
4 |
3 |
5 |
2 |
1 |
3 |
2 |
1 |
5 |
0 |
4 |
3 |
5 |
4 |
1 |
3 |
0 |
11 |
0 |
4 |
10 |
1 |
5 |
0 |
2 |
8 |
3 |
7 |
9 |
2 |
8 |
10 |
5 |
9 |
0 |
4 |
13 |
0 |
4 |
10 |
12 |
3 |
9 |
11 |
4 |
10 |
1 |
3 |
7 |
0 |
2 |
8 |
12 |
1 |
5 |
17 |
0 |
4 |
10 |
12 |
16 |
5 |
7 |
13 |
2 |
6 |
8 |
12 |
1 |
3 |
9 |
13 |
15 |
2 |
Имеем остатки от деления на 3: {0,1} нет 2;
от деления на 5: {0,1,2,4} – нет 3;
от деления на 7: {0,1,2,3,4,5}- нет 6;
от деления на 11: {0,1,2,3,4,5,7,8,9,10} – нет 6;
от деления на 13: {0,1,2,4,5,7,8,9,10,11,12} – нет 6;
от деления на 17: {0,1,2,3,4,5,6,7,8,9,10,12,13,15,16} – нет 11 и 14.
Чтобы ни одно из 18 чисел
p,p+4,p+10,p+12,p+16,p+22,p+24,p+30,p+36,p+40,p+42,p+46,p+52,p+54,p+60,p+64,p+66,p+70
не делилось ни на одно из чисел {3,5,7,11,13,17} нужно чтобы число p удовлетворяло системе равенств
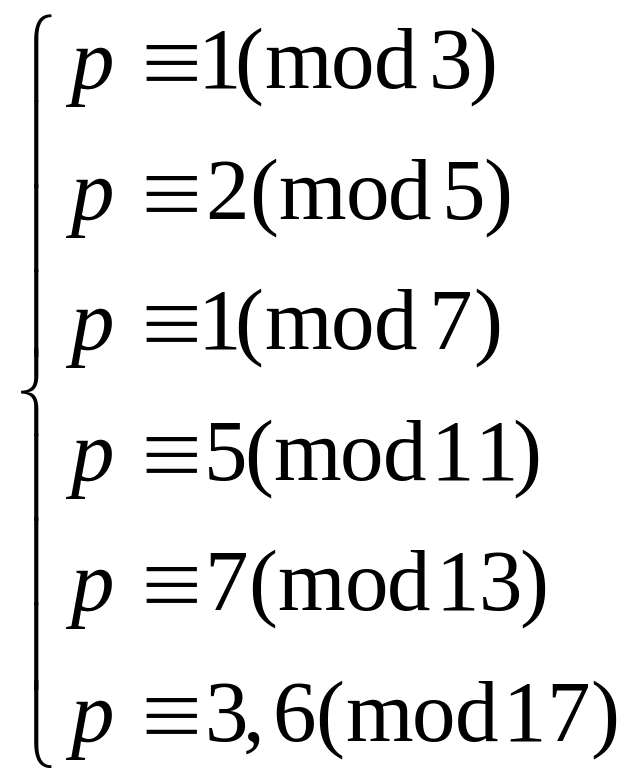Получилось
две системы, мы их записали в виде одной.
Мы приравниваем “p” к такому остатку, чтобы p, при сложении с имеющимися остатками, не давал нуля по соответствующему модулю. Например, по модулю 11 нет остатка 6, поэтому нужно приравнивать “p” к 5, т.к. 5 при сложении с 6 дает 0 по модулю 11, а остальные остатки при сложении с 5 нуля не дают. Значит, ни одно из 18 чисел не будет делиться на 11 и т.д.
Решаем систему.
Из первого уравнения получаем
.
Подставляем это равенство во второе уравнение:
.
Следовательно,
.
Подставляем это равенство в третье уравнение:
.
Таким образом,
.
Подставляем в четвертое уравнение:
.
Поэтому
.
Подставляем в пятое уравнение:
.
Значит,
.
Осталось подставить в последнее уравнение:
.
Получаем два решения шестого уравнения:
;
.
Теперь получаем решения наших систем:
;
.
Получаем два решения 38032 и 113107 по модулю 255255.
Поскольку число p должно
быть простым, в частности, нечетным, то
нужно добавить еще одно равенство
.
Окончательные решения: 113107 и 293287 по модулю 510510.
Поскольку было много вычислений, то нужно сделать проверку.
Проверка показывает, что решения правильные!
Итак, мы будем искать решения среди чисел вида
где q – любое натуральное число. Из каждого миллиона чисел нам нужно проверять всего 4 числа.