3.4.3. Анализ и прогнозирование на основе многофакторных моделей

Важную роль при оценке влияния факторов играют коэффициенты регрессионной модели. Однако непосредственно с их помощью нельзя сопоставить факторы по степени их влияния на зависимую переменную из-за различия единиц измерения и разной степени колеблемости. Для устранения таких различий при интерпретации применяются коэффициенты эластичности Э_j, а также бета- и дельта-коэффициенты

Эластичность У по отношению к X_j определяется как процентное изменение Y, отнесенное к соответствующему процентному изменению X, В общем случае эластичности не постоянны, они различаются, если измерены для различных точек на линии регрессии. По умолчанию стандартные программы, оценивающие эластичность, вычисляют ее в точках средних значений:

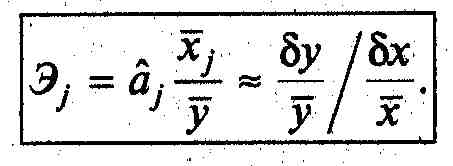
Эластичность не нормирована и может изменяться от - до +. Важно, что она безразмерна, так что интерпретация эластичности = 2 означает, что если X_j изменится на 1%, это приведет к изменению у на 2%. Если -0,5, это означает, что увеличение х_} на 1% приведет к уменьшению у на 0,5%. Высокий уровень эластичности означает сильное влияние независимой переменной на объясняемую переменную. Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении j-го фактора на 1%. Однако он не учитывает степень колеблемости факторов.

Бета-коэффициент

(1)

где — среднеквадратическое отклонение j-го фактора. Стандартные отклонения вычисляются по формулам

(2)

Бета-коэффициент показывает, на какую часть величины среднеквадратического отклонения S_у изменится зависимая переминая У, если соответствующая независимая переменная X, изменится на величину своего среднеквадратического отклонения при фиксированном значении остальных независимых переменных.

Указанные коэффициенты позволяют упорядочить факторы по степени их влияния на зависимую переменную.

Долю влияния каждого фактора в суммарном влиянии всех факторов можно оценить по величине дельта - коэффициентов:

(3)

Где — коэффициент парной корреляции между j-м фактором (j=1,2.. k) и зависимой переменной.

Одна из важнейших целей моделирования заключается в прогнозировании поведения исследуемого объекта. Обычно термин «прогнозирование» используется в тех ситуациях, когда требуется предсказать состояние системы в будущем. Для регрессионных моделей он имеет, однако, более широкое значение. Как уже отмечалось, данные могут не иметь временной структуры, но и в этих случаях может возникнуть необходимость оценки значения зависимой переменной для некоторого набора независимых, объясняющих переменных, которых нет в исходных наблюдениях. Именно в этом смысле — как построение оценки зависимой переменной — и следует понимать прогнозирование в эконометрике.

При использовании построенной модели для прогнозирования делается предположение о сохранении в Период прогнозирования существовавших ранее взаимосвязей переменных.

Для прогнозирования зависимой переменной необходимо знать прогнозные значения всех входящих в нее факторов. Их оценки могут быть получены на основе временных экстраполяционных моделей или заданы пользователем. Эти оценки подставляются в модель и получаются прогнозные оценки.

Для того чтобы определить область возможных значений результативного показателя при рассчитанных значениях факторов, следует учитывать два возможных источника ошибок:

• рассеивание наблюдений относительно линии регрессии. Эти ошибки измеряются с помощью характеристик точности, в частности величиной S_e ;

• ошибки, обусловленные математическим аппаратом построения самой линии регрессии. Возникают вследствие фиксации численного значения коэффициентов регрессии, в то время как в действительности они являются случайными, нормально распределенными.

Для линейной модели регрессии доверительный интервал рассчитывается следующим образом. Оценивается величина отклонения от линии регрессии (обозначим ее U)

: (4)

где . Здесь штрих обозначает транспонирование матрицы. Здесь умножение Х на транспонированную матрицу производится для получения квадратной матрицы. так как только для квадратной матрицы можно найти обратную. Сама матрица Х в общем случае является столбцом с размерностью k.

Пример 1. Имеются следующие статистические данные об одном из продуктов фирмы (табл. 1); Построить модель для предсказания объема реализации этого продукта.

1. Осуществить выбор факторных признаков для построения двухфакторной регрессионной модели.

2. Рассчитать параметры модели.

3. Для оценки качества модели определить линейный коэффициент множественной корреляции и коэффициент детерминации.

4. Осуществить оценку значимости уравнения регрессии.

5. Оценить с помощью t-критерия Стьюдента статистическую значимость коэффициентов уравнения множественной регрессии.

6. Оценить влияние факторов на зависимую переменную по модели.

7. Построить точечный и интервальный прогноз результирующего показателя на два месяца вперед

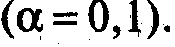
Создайте на первом листе таблицу 1

Объем реализации товара, млн. руб.	Месяц	Расходы на рекламу, тыс. руб.	Цена товара, руб.	Цена товара у конкурента, руб.	Индекс потребительских расходов, %
126	1	4	15	17	100
137	2	4,8	14,8	17,3	98,4
148	3	3,8	15,2	16,8	101,2
191	4	8,7	15,5	16,2	103,5
274	5	8,2	15,5	16	104,1
370	6	9,7	16	18	107
432	7	14,7	18,1	20,2	107,4
445	8	18,7	13	15,8	108,5
367	9	19,8	15,8	18,2	108,3
367	10	10,6	16,9	16,8	109,2
321	11	8,6	16,3	17	110,1
307	12	6,5	16,1	18,3	110,7
331	13	12,6	15,4	16,4	110,3
345	14	6,5	15,7	16,2	111,8
364	15	5,8	16	17,7	112,3
384	16	5,7	15,1	16,2	112,9

Решение.

1. Выберем факторные признаки для построения двухфакторной ■ регрессионной модели.

Объем реализации — это зависимая переменная Y. В качестве независимых, объясняющих переменных выбраны: время X₁ расходы на рекламу X₂, цена товара X₃, средняя цена товара у конкурентов Х₄, индекс потребительских расходов X_5.

Необходимо провести корреляционный анализ для оценки степени взаимного влияния объясняющих переменных и зависимой переменной.

Для проведения корреляционного анализа используем инструмент Корреляция (Анализ данных в Excel):

• Выберите команду Сервис => Анализ данных.

■ В диалоговом окне Анализ данных выберите инструмент Кор реляция, затем нажмите кнопку ок.

В диалоговом окне корреляция в поле Входной интервал введите диапазон ячеек, содержащих исходные данные А1:F17. Так как указаны и заголовки столбцов, то установите флажок «Метки впервой строке».

• Выберите параметры вывода (Укажите — Новый рабочий лист).

• Нажмите кнопку ok,

В результате перечисленных действий будет получена матрица коэффициентов парной корреляции (рис. 1).

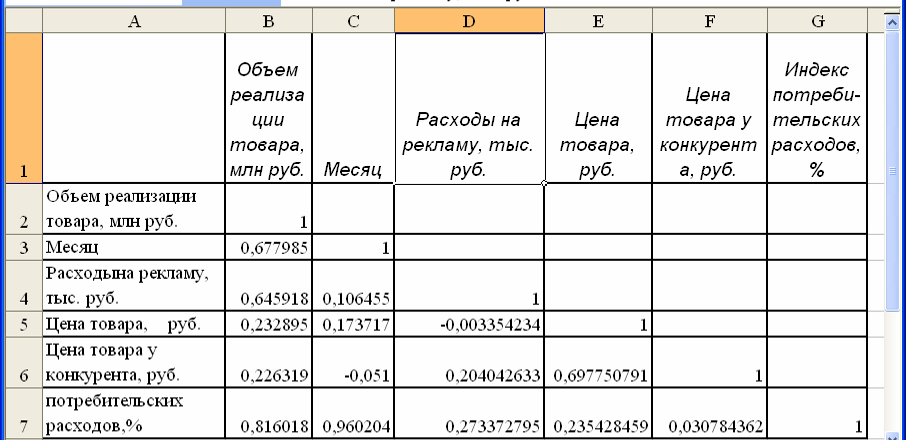
Рис. 1

Чтобы в вашей работе она выглядела, так как на рис 1, для заголовков в Формате установите «Переносить по словам».

Линейный коэффициент парной корреляции r_xy для линейной регрессии изменяется в диапазоне ( ) и вычисляется по формуле:

(5)

Пояснения к корреляционной матрице. Эта матрица симметрична, поэтому показана только её нижняя часть. Ниже на рис. 2 дана её структура.

Y	ryy
X1	ryx1	rx1x1
X2	ryx2	rx1x2	rx2x2
X3	ryx3	rx1x3	rx2x3	rx3x3
X4	ryx4	rx1x4	rx2x4	rx3x4	rx4x4
X5	ryx5	rx1x5	rx2x5	rx3x5	rx4x5	rx5x5

Рис. 2. Структура корреляционной матрицы

Коэффициенты корреляции r_yy, r_x1x1, r_x2x2 и так далее равны единице. Так как в этом случае и числитель и знаменатель равен дисперсиям соответственно. Во всех других случаях коэффициент корреляции для стохастических зависимостей по абсолютной величине меньше единицы.

Анализ матрицы коэффициентов парной корреляции показывает, что зависимая переменная Y (т.е. объем реализации) имеет тесную связь с индексом потребительских расходов ( 0,816), с расходами на рекламу (r_yx2 = 0,646) и со временем r_yx1= 0,678). А факторы х₃ и х_4. имеют слабую взаимосвязь с параметром Y, поэтому их можно исключить из рассмотрения.

Однако факторы X₁ и X₅ тесно связаны между собой ( ₌ = 0,96 > 0,8), что свидетельствует о наличии мультиколлинеарности параметров X₁ и X₅. То есть они находятся в очень тесной взаимосвязи, поэтому один из параметров можно исключить из корреляционной зависимости. Обычно оставляют тот параметр, который можно изменять или тот, который оказывает наиболее сильное влияние. В данном случае ни один из параметров не подается управлению, поэтому, из этих двух переменных оставим в модели Х₅ — индекс потребительских расходов, так как он имеет более тесную корреляционную связь с Y (r_yx5=0,816). В этом примере число наблюдений п = 16, число начальных объясняющих параметров т = 5, после исключения незначимых факторов п = 16, а число параметров уравнения регрессии k = 2.

Линейная модель множественной регрессии в общем случае имеет вид системы, состоящей из n уравнений:

(6)

где n – число рассматриваемых событий (число членов в выборке);

случайная составляющая, равная разности расчётных и фактических значений;

k - количество включенных в модель факторов.

Коэффициент регрессии показывает, на какую величину в среднем изменится результативный признак Y, если переменную Х_j увеличить на единицу измерения, т.е. a_j. является нормативным коэффициентом.

Анализ уравнения (6) и методика определения параметров становятся более наглядными, а расчетные процедуры существенно упрощаются, если воспользоваться матричной формой записи многопараметрического уравнения регрессии:

(7)

где Y— это вектор зависимой переменной размерности п х 1, представляющий собой, п наблюдений значений у_i; X — матрица п наблюдений независимых переменных X₁, Х₂, ..., Х_к, размерность матрицы X равна пх(k+1);

а - подлежащий оцениванию вектор неизвестных параметров размерности

(k +1)х1;

— вектор случайных отклонений (возмущений) размерности п х 1.

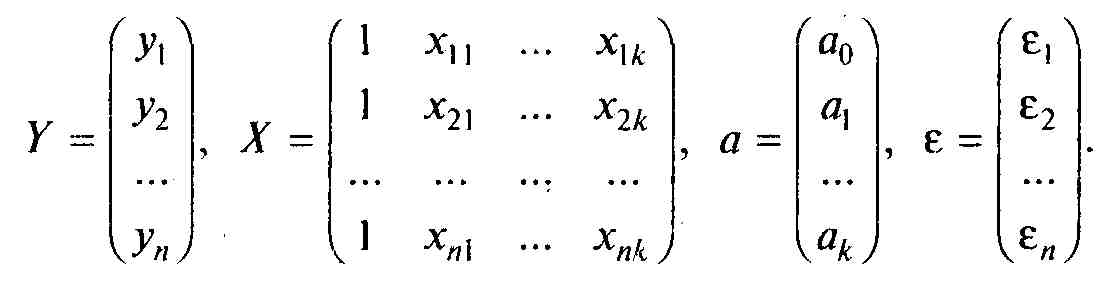
Уравнение (7) содержит значения неизвестных параметров а₀, а₁, а₂,..., a_k. Эти величины оцениваются на основе выборочных наблюдений, поэтому полученные расчетные показатели не являются истинными, а представляют собой лишь их статистические оценки.

Модель линейной регрессии, в которой вместо истинных значений параметров подставлены их оценки (а именно такие регрессии и применяются на практике), имеет вид

где А — вектор оценок параметров; e — вектор «оцененных» отклонений регрессии, остатки регрессии e = У- ХА; — оценка значений Y, равная ХА.

Оценка параметров модели множественной регрессии проводится с помощью метода наименьших квадратов. Формулу для вычисления параметров регрессионного уравнения приведем без вывода:

(8)

Здесь - означает транспонирование матрицы.

Для получения коэффициентов двухпараметрической линии регрессии рассматривают каждое событие из выборки, состоящей из n (в нашем случае n=16) и определяют коэффициенты .

2. Рассчитаем параметры модели. Оценка параметров регрессии осуществляется методом наименьших квадратов по формуле (8) с использованием данных, приведенных в табл. 1, которую скопируем на второй лист и уберем незначащие и мультиколлинеарные параметры (для вычисления а₀ добавлен столбец Х₀). Вид трансформированной таблицы показан на табл. 2

					Таблица 2
Объем реализации Y	X0			Реклама Х1	Индекс потребительских расходов Х2
126	1			4	100
137	1			4,8	98,4
148	1			3,8	101,2
191	1			8,7	103,5
274	1			8,2	104,1
370	1			9,7	107
432	1			14,7	107,4
445	1			18,7	108,5
367	1			19,8	108,3
367	1			10,6	109,2
321	1			8,6	110,1
307.	1			6,5	110,7
331		1	12,6			110,3
345		1	6,5			111,8
364		1	5,8			112,3
384		1	5,7			112,9

Итак, найдите параметры уравнения

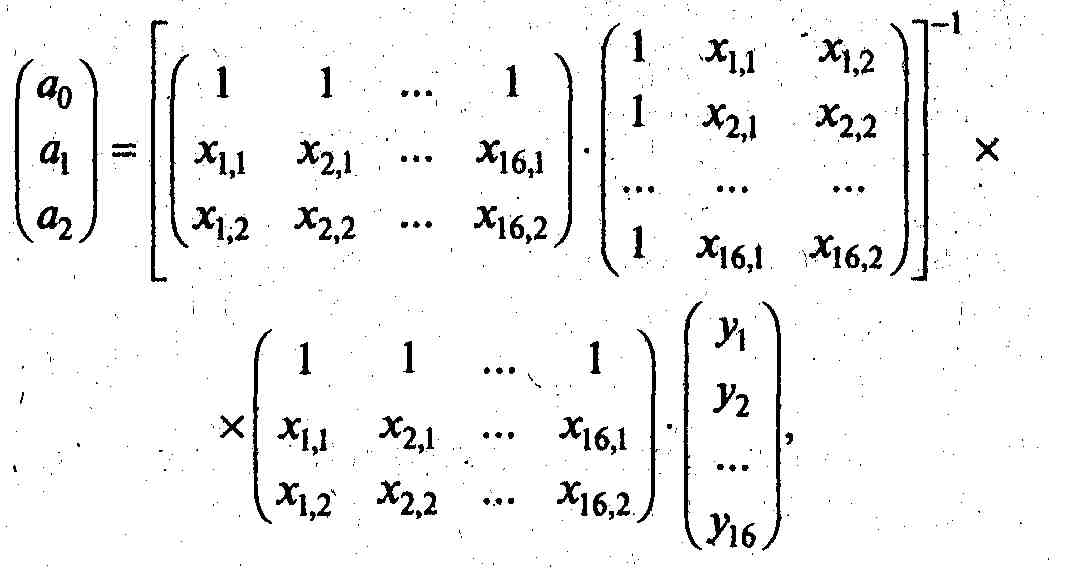
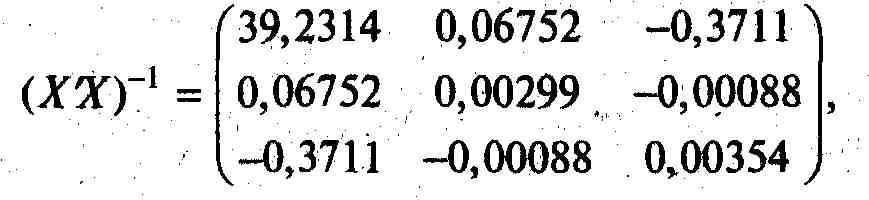
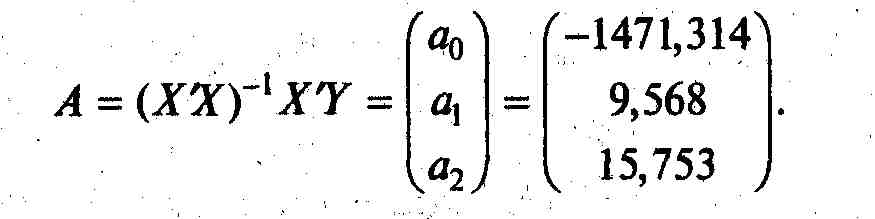
Сначала произведите транспонирование матрицы Х, затем умножьте , полученное значение обратите (найдите обратную матрицу). Затем умножьте . После этого найдите матрицу столбец A. При транспонировании и умножении матриц используются формулы массива. Не забывайте, что нужно выделять ровно столько ячеек, какой ожидается результат. Например, при транспонировании матрицы 16х3, должна получиться матрица 3х16. Поэтому следует выделять именно такой диапазон ячеек.

Все действия с матрицами можно провести сразу, выделив только три ячейки под матрицу искомых коэффициентов А, но в этом случае нужно научиться пользоваться вместо клавиши Enter зелёной галочкой, расположенной около кнопки вызова мастера функций f(x) и повторно вызывать мастер функций щелчком по этой кнопке. Кроме того, нужно правильно расставлять скобки для обеспечения правильной последовательности вычислений.

Уравнение регрессии зависимости объема реализации от затрат на рекламу и индекса потребительских расходов можно записать в следующем виде, используя полученные коэффициенты :

Расчетные значения Y определяются путем последовательной подстановки в эту модель значений факторов, взятых для каждого наблюдения.

Для проведения регрессионного анализа используем инструмент Регрессия (Анализ данных в Excel):

• Выберите команду Сервис => Анализ данных.

• В диалоговом окне Аанализ данных выберите инструмент Регрессия, затем нажмите кнопку ок.

• В диалоговом окне Регрессия в поле Входной интервал у введите адрес одного диапазона ячеек, который представляет зависимую переменную. В поле входной интервал X введите адреса одного или нескольких диапазонов, которые содержат значения независимых переменных (рис. 3).

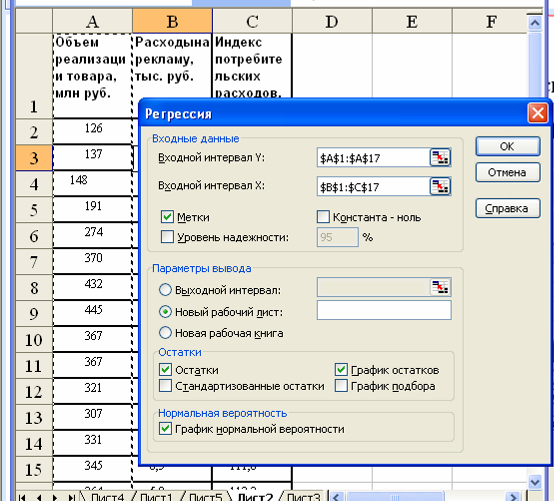
Рис. 3. Диалоговое окно Регрессия подготовлено к выполнению анализа данных

• Если выделены и заголовки столбцов, установите флажок Метки в первой строке.

• Выберите параметры вывода (в данном примере — Новая рабочая книга).

• В ноле Остатки поставьте необходимые флажки.

• Нажмите кнопку ОК.

В результате Перечисленных действий будет получен протокол выполнения регрессионного анализа (рис. 4).

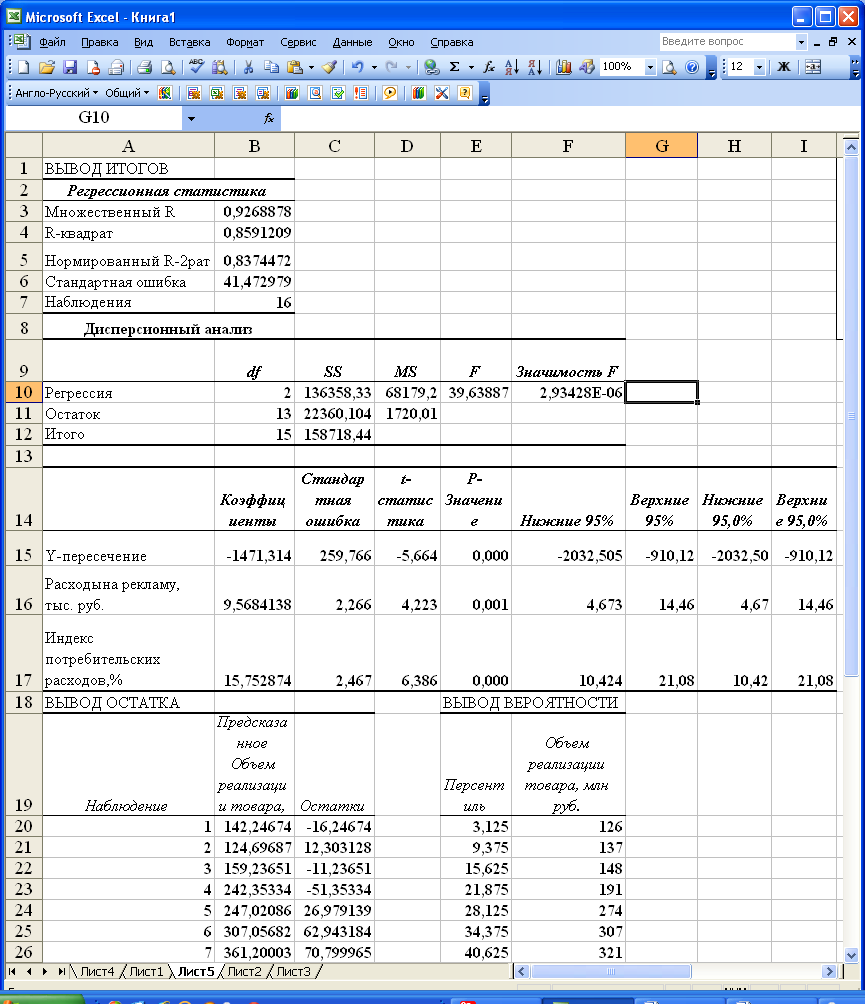
Рис. 4 Протокол выполнения регрессионного анализа. Остатки показаны не полностью.

Рассмотрим содержание протокола регрессионного анализа (см. рис.4.), в котором отражены основные итоги расчетов. Пояснения таблицы «Регрессионная статистика» приведены в табл. 3, а «Дисперсионной анализ» — в табл. 4.

Таблица 3

Таблица.4

В таблице, следующей за таблицей «Дисперсионный анализ» (см. рис. 4), во втором столбце содержатся коэффициенты уравнения регрессии а₀, а₁, а₂, в третьем столбце — стандартные ошибки коэффициентов уравнения регрессии, а в четвертом — t-статистика, используемая для проверки значимости коэффициентов уравнения регрессии. где S_a. — это стандартное (среднеквадратическое) отклонение коэффициента уравнения регрессии а_j.

Как видно, получено уравнение регрессии зависимости объема реализации от затрат на рекламу и индекса потребительских расходов точно такое же, что и ранее полученное в результате громоздких матричных вычислений.

3. Оценим качество модели. В таблице «Вывод остатка» (см. рис. 4) приведены вычисленные (предсказанные) по модели значения зависимой переменной Y (столбец «Предсказанное») и значения остаточной компоненты е_i (столбец «Остатки»).

Значение коэффициентов детерминации и множественной корреляции можно найти в таблице «Регрессионная статистика» (см. рис. 4). Коэффициент детерминации

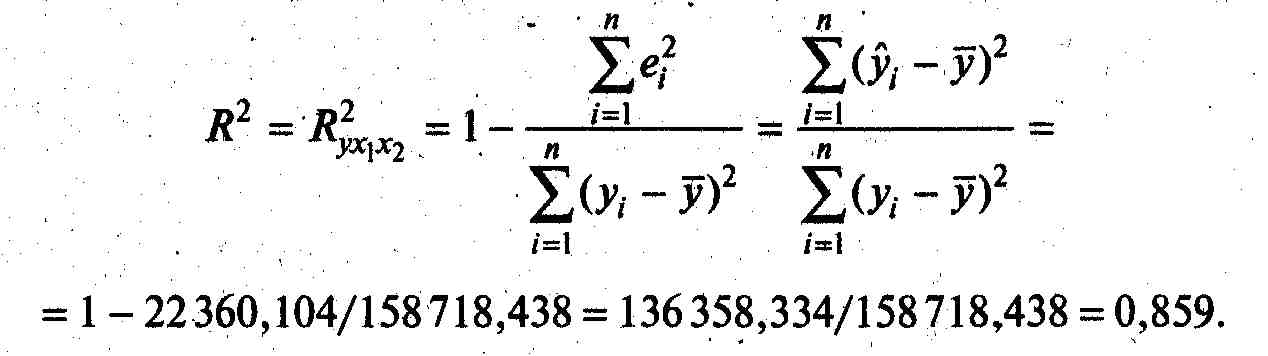
Коэффициент детерминации показывает, что около 86% вариации зависимой переменной учтено в модели и обусловлено влиянием включенных факторов.

Коэффициент множественной корреляции

Он показывает высокую тесноту связи зависимой переменной Y с двумя включенными в модель объясняющими факторами.