
- •Введение.
- •Логическая структура современной физики.
- •Границы применимости физической теории.
- •Глава 1. Основные понятия и законы классической механики.
- •§2. Классические представления о пространстве и времени и их арифметизация.
- •§3. Кинематические и динамические характеристики механического движения.
- •§4. Законы динамики Ньютона.
- •§5. Принцип относительности Галилея.
- •§ 6. Основная задача динамики и роль начальных условий. Принцип причинности классической механики.
- •§ 7. Потенциальная энергия и классификация свободных механических систем.
- •Глава. 2. Законы сохранения и принцип симметрии.
- •§ 8. Первые интегралы уравнений движения и законы сохранения.
- •§ 9. Закон сохранения энергии и его связь с однородностью времени.
- •§ 10. Закон сохранения импульса и его связь с однородностью пространства.
- •§ 11. Закон сохранения момента импульса и его связь с изотропностью пространства.
- •Глава 3. Основы аналитической механики.
- •§ 12. Постановка задачи о движении несвободной механической системы. Классификация связей.
- •13. Уравнения Лагранжа. Функция Лагранжа.
- •С учетом (13.12) перепишем уравнения (13.11) в окончательном виде
- •§ 14. Функция Лагранжа и законы сохранения.
- •§ 15. Основная задача вариационного исчисления. Уравнения Эйлера.
- •Простейшим функционалом является криволинейный интеграл
- •Интегрируя второй интеграл в правой части (15.6) по частям с учетом предельных условий (15.4) получаем:
- •Обобщим полученные результаты для функционала
- •§ 16. Принципы наименьшего действия Гамильтона-Остроградського.
- •§ 17. Канонические уравнения движения.
- •Подставляя (17.8) в (17.7), получаем
- •§ 18. Скобоки Пуассона.
- •§ 19. Уравнение Гамильтона-Якоби.
Обобщим полученные результаты для функционала
 ,
(15.10)
,
(15.10)
зависящего
от S
независимых
функций
 и их производных
и их производных
 .
Основная
вариационная задача
в применении к (15.10) состоит в нахождении
такого набора функций
.
Основная
вариационная задача
в применении к (15.10) состоит в нахождении
такого набора функций
 ,
которые: 1) реализуют экстремум функционала
(15.10) и 2) удовлетворяют граничным условиям
,
которые: 1) реализуют экстремум функционала
(15.10) и 2) удовлетворяют граничным условиям
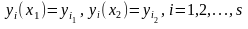 ,
(15.11)
,
(15.11)
где
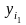 ,
,
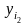 - заданные
величины.
- заданные
величины.
В
полной аналогии с предыдущим, строим
новые функции
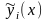 ,
близкие
к
:
,
близкие
к
:
 ,
(15.12)
,
(15.12)
где
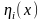 - произвольные
функции, удовлетворяющие граничным
условиям
- произвольные
функции, удовлетворяющие граничным
условиям
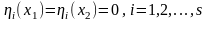 ,
(15.13)
,
(15.13)
и
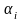 - малые
численные параметры. Сводим задачу к
отысканию экстремума функции
- малые
численные параметры. Сводим задачу к
отысканию экстремума функции
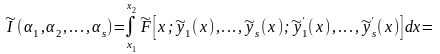
 . (15.14)
. (15.14)
Условие экстремума функции (15.14) можно записать в виде
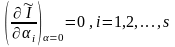 ,
(15.15)
,
(15.15)
где
мы обозначим
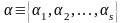 .
Умножая каждое i-тое
равенство (15.15) на
и складывая полученные результаты
почленно, получаем следующую эквивалентную
запись условия экстремума в виде одного
уравнения:
.
Умножая каждое i-тое
равенство (15.15) на
и складывая полученные результаты
почленно, получаем следующую эквивалентную
запись условия экстремума в виде одного
уравнения:
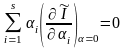 .
(15.16)
.
(15.16)
Подставляя сюда (15.14) и используя правило дифференцирования интеграла по параметру, перепишем (15.16) следующим образом:
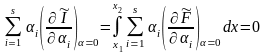 (15.17)
(15.17)
Для подынтегральной функции в левой части (15.17) имеем:
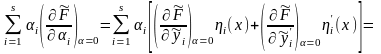
 .
(15.18)
.
(15.18)
Подставляя (15.18) в (15.17) и интегрируя во втором интеграле по частям с учетом граничных условий (15.13), получаем:
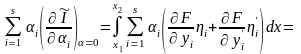
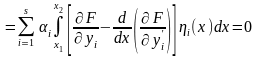 .
(15.19)
.
(15.19)
В силу произвольности функций из (15.19) следует вывод: функции , реализующие экстремум функционала (15.10), должны удовлетворять системе уравнений Эйлера
 .
(15.20)
.
(15.20)
Полученные
результаты можно сформулировать в
несколько другом (эквивалентном)
виде, если воспользоваться понятием
вариации
функции и
вариации
функционала.
В полном соответствии с определением
вариации функции в § 12, мы определяем
вариации
 функций
согласно (15.12) следующим образом:
функций
согласно (15.12) следующим образом:
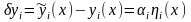 .
(15.21)
.
(15.21)
Варьирование
любой функции
влечет за собой варьирование и ее
производной
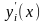 ;
вариацию
;
вариацию
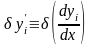 мы согласно (15.14) определяем
формулой
мы согласно (15.14) определяем
формулой
 (15.22)
(15.22)
Из определений (15.21) и (15.22) следует важное правило вычисления вариаций: операции варьирования и дифференцирования перестановочны, т.е.
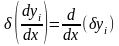 .
(15.23)
.
(15.23)
Действительно,
дифференцируя по
 равенство
(15.21)
равенство
(15.21)
 ,
,
и сравнивая этот результат с (15.22), получаем (15.23).
В
результате варьирования функций
и их производных
получает приращение и любая функция
вида
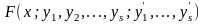 ;
вариацией
;
вариацией
 функции
функции
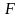 называется линейная
по
и
называется линейная
по
и
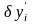 часть
приращения
часть
приращения
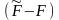 этой функции, т.е.
этой функции, т.е.
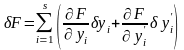 .
(15.24)
.
(15.24)
(Для
получения (15.24) нужно разложить
 в ряд по
и
и ограничиться для
первым не исчезающим слагаемым).
в ряд по
и
и ограничиться для
первым не исчезающим слагаемым).
Напомним,
что в соответствии с (15.14),

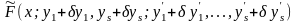 .
Правые части равенств (15.24) и (15.18) равны
(с учетом (15.21) и (15.22)), поэтому формула
.
Правые части равенств (15.24) и (15.18) равны
(с учетом (15.21) и (15.22)), поэтому формула
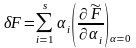 (15.25)
(15.25)
дает эквивалентное (15.24) определение вариации функции .
По
аналогии с (15.25), первой
вариацией функционала
(15.10) или просто вариацией
функционала
(15.10) называют величину
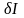 ,
определяемую выражением
,
определяемую выражением
 (15.26)
(15.26)
Определение (15.26) позволяет переписать результат (15.19) в виде
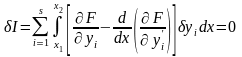 .
(15.27)
.
(15.27)
Тем
самым мы получили другую
формулировку результата решения основной
вариационной задачи:
функции
,
 ,
реализующие экстремум функционала
(15.10), должны
обращать в нуль вариацию функционала
.
Это утверждение, как видно из (15.27),
равносильно требованию (15.20); действительно,
так как функции
независимы,
то
.
Также независимы
и, следовательно, произвольны, поэтому
равенство
,
реализующие экстремум функционала
(15.10), должны
обращать в нуль вариацию функционала
.
Это утверждение, как видно из (15.27),
равносильно требованию (15.20); действительно,
так как функции
независимы,
то
.
Также независимы
и, следовательно, произвольны, поэтому
равенство
 имеет место только при выполнении
уравнений Эйлера (15.20).
имеет место только при выполнении
уравнений Эйлера (15.20).
Определение (15.25) и (15.26) позволяют «извлечь» из (15.17) важное правило: операции варьирования и интегрирования перестановочны, т.е.
 .
(15.28)
.
(15.28)
Замечание. По аналогии с определением (15.24) можно дать другое (эквивалентное (15.26)) определение первой вариации функционала: вариацией функционала (15.10) называется линейная (главная) часть приращения
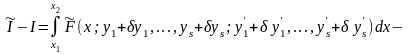
 ,
(15.29)
,
(15.29)
которое
получает функционал
 вследствие вариации функций
и их производных
в подынтегральном выражении (отметим
здесь, что в физической литературе
иногда вариацией
называют само приращение (15.29), т.е.
величину
вследствие вариации функций
и их производных
в подынтегральном выражении (отметим
здесь, что в физической литературе
иногда вариацией
называют само приращение (15.29), т.е.
величину
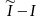 ,
что математически некорректно). Для
получения явного выражения для
разложим функцию
в (15.29) в ряд по степеням
и
и ограничимся в этом разложении только
членами первого порядка малости (тем
самым мы и получаем линейную часть
разности
):
,
что математически некорректно). Для
получения явного выражения для
разложим функцию
в (15.29) в ряд по степеням
и
и ограничимся в этом разложении только
членами первого порядка малости (тем
самым мы и получаем линейную часть
разности
):

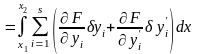 .
(15.30)
.
(15.30)
Учитывая определения (15.24) и (15.25), приходим к выводу, что определение вариации функционала (15.30) эквивалентно определению (15.26). Заметим, что определение (15.30) с учетом (15.24) фактически совпадает со свойством операции варьирование (15.28).
