С учетом (13.12) перепишем уравнения (13.11) в окончательном виде

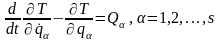. (13.13)

Эти уравнения называются уравнениями Лагранжа второго рода или просто уравнениями Лагранжа. Они справедливы для любой механической системы с идеальными голономними и удерживающими связями.

Неизвестными в этих уравнениях есть функции 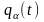, которые однозначно определяющие положение системы в просторные (причем число неизвестных равно числу уравнений). Большое преимущество уравнений Лагранжа состоит в том, что их число равно числу степеней свободы системы и не зависит от количества входящих в систему точек и тел. Например, машины и механизмы состоят из многих тел (деталей), а имеют обычно одну-две ступени свободы; следовательно, изучение их движения потребует составления лишь одного-двух уравнений Лагранжа (поэтому они широко используются в динамике машин и механизмов, в теории колебаний, теории гироскопа и т.д.).

Методика применения уравнений Лагранжа к решению конкретных задач состоит из следующих шагов: 1) выбираются обобщенные координаты системы (для сложных систем – это нетривиальная задача); 2) находится явное выражение для 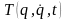и с помощью (13.10) по заданным силам 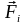определяются обобщенные силы ; 3) составляются уравнения (13.13) в явном виде (после подстановки в левой части уравнения (13.13) будут содержать 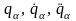, т.е. будут обыкновенными дифференциальными уравнениями второго порядка относительно неизвестных ); 4) интегрируя эти уравнения и определяя постоянные интегрирования по начальным или краевым условиям, находят зависимости , т.е. закон движения системы в обобщенных координатах (при необходимости с помощью (13.13) находят затем координатную форму закона движения системы ).

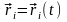Замечание 1. Уравнения Лагранжа (13.13) имеют большое значение также и для динамики свободных механических систем, по отношению к которым они совпадают с уравнениями движения Ньютона, записанными в произвольной (зависящей от выбора обобщенных координат) системе криволинейных координат (доказательство этого утверждения мы опускаем).

Замечание 2. Следует иметь в виду, что выбор обобщенных координат системы неоднозначен: если q и - два набора обобщенных координат одной и той же системы, то эти наборы есть однозначные функции друг друга вида

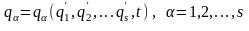(13.14)

Преобразование (13.14) от одного набора обобщенных координат q к другому набору называют точечным преобразованием. Подставляя (13.14) в (13.13), получаем новое однозначное представление через :

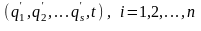(13.15)

Ясно, что если теперь переходить в уравнении (13.12) к обобщенным координатам с помощью (13.15), то получим уравнения Лагранжа той же формы, что и (13.13), но только в штрихованных координатах. Т.о., уравнения Лагранжа инвариантные относительно точечных преобразований (13.14).

Исследуем теперь более подробно структуру уравнений Лагранжа (13.13) для различных классов (см. § 7) механических систем. Эта структура определяется конкретным видом обобщенных сил и кинетической энергией Т. Рассмотрим вначале зависимость формы (13.13) от вида функций .

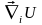Пусть все активные силы (как внутренние так и внешние) являются потенциальными, т.е. =- , где 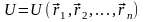- полная потенциальная энергия системы (см. § 7). Подставляя сюда (13.3), т.е. рассматривая U как неявную функцию обобщенной силы (13.10), имеем:

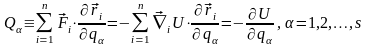, (13.16)

где , а зависимость от есть результат нестационарности связей. Очевидно, что не зависит от обобщенных скоростей , т.е.

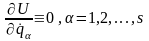. (13.17)

С учетом (13.16) и (13.17) уравнения Лагранжа (13.13) можно представить в виде

,

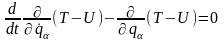или

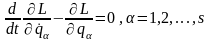, (13.18)

где функция обобщенных координат , обобщенных скоростей и времени вида

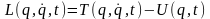(13.19)

называется функцией Лагранжа механической системы. Хотя здесь функцию Лагранжа (13.19) мы ввели формальным образом с целью записи уравнений Лагранжа (13.13) для механических систем с потенциальными активными силами в форме (13.18), однако в § 14 мы покажем, что 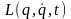является важнейшей функцией состояния механической системы.

Замечание 1. Легко убедиться, что к виду (13.18) уравнения Лагранжа (13.13) приводятся также и для класса механических систем с обобщенно-потенциальными силами, т.е. для таких систем, обобщенные силы которых можно представить в виде

, (13.20)

где 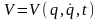- так называемый обобщенный потенциал, или потенциал, зависящий от скорости. Функция Лагранжа для указанных систем определяется как разность кинетической энергии системы и ее обобщенного потенциала, т.е.

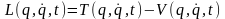. (13.21)

Важнейшим примером системы с обобщенно-потенциальными силами является система заряженных частиц, движущихся во внешнем электромагнитном поле. Например, в виде (13.20) можно представить силу Лоренца (см. часть II этого курса).

Замечание 2. Если на механическую систему наряду с потенциальными (или обобщенно-потенциальными) активными силами действуют и диссипативные силы (т.е. силы приводящие к рассеянию механической энергии системы), то при записи уравнений Лагранжа (13.13) поступают следующим образом. Каждую обобщенную силу разбивают на две части:

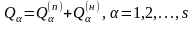, (13.22)

где (или )

- обобщенные силы, обусловленные действием на систему только потенциальных (или обобщенно-потенциальных) сил, и

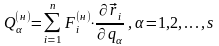, (13.23)

• обобщенные силы, возникающие в результате действия на систему непотенциальных диссипативных сил вязкого трения. Легко видеть, что уравнения Лагранжа (13.13) в этом случае можно представить в виде

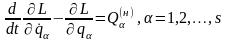, (13.24)

где (или ).

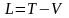Рассмотрим теперь структуру кинетической энергии 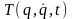несвободной системы и ее влияние на вид . По определению (см. § 3 и § 9) кинетическая энергия любой системы является однородной и положительно определенной квадратичной формой скоростей материальных точек системы. Однако кинетическая энергия несвободной системы в общем случае оказывается неоднородной квадратичной формой относительно обобщенных скоростей системы.

Действительно, подставляя (13.6) в определение 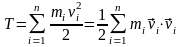кинетической энергии, получаем:

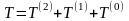, (13.25)

где

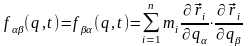, , (13.26)

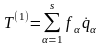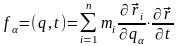, , (13.27)

. (13.28)

Таким образом, из (13.25) – (13.28) видно, что нестационарность связей, налагаемых на механическую систему, приводит к двум эффектам: 1) 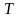оказывается неоднородной квадратичной формой ; 2) как так и 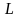системы становятся явно зависимыми от времени.

В случае, когда на систему наложены только стационарные связи, а все активные силы, действующие на нее, являются потенциальными, то 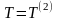, и функцию Лагранжа системы можно представить в виде (см. (13.19) и (13.26))

. (13.29)

Так как рассматриваемой системы есть однородная квадратичная форма от , то полезно следующее

математическое замечание. Если - однородная функция порядка n, то имеет место равенство (теорема Эйлера)

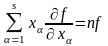. (13.30)

Действительно, функция называется однородной порядка n, если

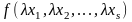= . (13.31)

Дифференцируя (13.31) по , имеем

.

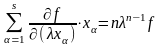Полагая здесь =1, мы приходим к (13.30).

На основании теоремы Эйлера (13.30) для кинетической энергии 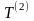имеем следующее равенство:

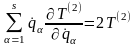, (13.32)

которым мы в дальнейшем воспользуемся.

Замечание. Важнейшее значение уравнений Лагранжа в форме (13.18) состоит в том, что при соответствующем обобщении понятий их можно использовать не только в механике, но и в других областях физики, например для изучения движения классических физических полей, т.е. систем с бесконечным числом степеней свободы.