
Внешние и внутренние силы
. В механике внешними силами по отношению к данной системе материальных точек (т. е. такой совокупности материальных точек, в которой движение каждой точки зависит от положений или движений всех остальных точек) называются те силы, к-рые представляют собою действие на эту систему других тел (других систем материальных точек), не включенных нами в состав данной системы. Внутренними силами являются силы взаимодействия между отдельными материальными точками данной системы. Подразделение сил на внешние и внутренние является совершенно условным: при изменении заданного состава системы некоторые силы, ранее бывшие внешними, могут стать внутренними, и обратно. Так, например, при рассмотрении
движения системы, состоящей из земли и ее спутника луны, силы взаимодействия между этими телами будут внутренними силами для этой системы, а силы притяжения солнца, остальных планет, их спутников и всех звезд будут внешними силами по отношению к указанной системе. Но если изменить состав системы и рассматривать движение солнца и всех планет как движение одной общей системы, то внешн. силами будут только силы притяжений, оказываемых звездами; все же силы взаимодействия между планетами, их спутниками и солнцем становятся для этой системы силами внутренними. Точно так же, если при движении паровоза выделим поршень парового цилиндра как отдельную систему материальных точек, подлежащую нашему рассмотрению, то давление пара на поршень по отношению к нему явится внешней силой, и то же давление пара будет одной из внутренних сил, если будем рассматривать движение всего паровоза в целом; в этом случае внешними силами по отношению ко всему паровозу, принятому за одну систему, будут: трение между рельсами и колесами паровоза, сила тяжести паровоза, реакция рельсов и сопротивление воздуха; внутренними силами будут все силы взаимодействия между частями паровоза, напр. силы взаимодействия между паром и поршнем цилиндра, между ползуном и его параллелями , между шатуном и пальцем кривошипа, и т. п. Как видим, по существу нет различия между внешними и внутренними силами, относительное же различие между ними определяется лишь в зависимости от того, какие тела мы включаем в рассматриваемую систему и какие считаем не входящими в состав системы. Однако указанное относительное различие сил имеет весьма существенное значение при исследовании движения данной системы; по третьему закону Ньютона (о равенстве действия и противодействия), внутренние силы взаимодействия между каждыми двумя материальными точками системы равны по величине и направлены по одной и той же прямой в противоположные стороны; благодаря этому при разрешении различных вопросов о движении системы материальных точек возможно исключить все внутренние силы из уравнений двшкения системы и тем самым сделать возможным самое исследование о движении всей системы. Этот метод исключения внутренних, в большинстве случаев неизвестных, сил связи имеет существенное значение при выводах различных законов механики системы.
Абсолютно упругий удар - соударение двух тел, в результате которого в обоих участвующих в столкновении телах не остается никаких деформаций и вся кинетическая энергия тел до удара после удара снова превращается в первоначальную кинетическую энергию (отметим, что это идеализированный случай). Для абсолютно упругого удара выполняются закон сохранения кинетической энергии и закон сохранения импульса. Обозначим скорости шаров массами m1 и m2 до удара через ν1 и ν2, после удара - через ν1' и ν2' (рис. 1). Для прямого центрального удара векторы скоростей шаров до и после удара лежат на прямой линии, проходящей через их центры. Проекции векторов скоростей на эту линию равны модулям скоростей. Их направления учтем знаками: положительное соотнесем движению вправо, отрицательное - движению влево.
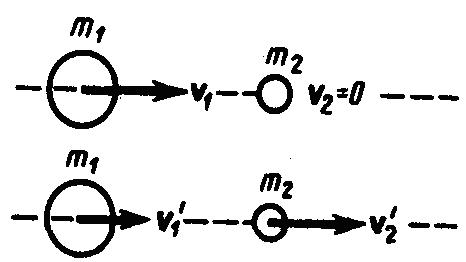
Рис.1
При указанных
допущениях законы сохранения имеют вид
![]() (1)
(1)
![]() (2)
Произведя соответствующие
преобразования в выражениях (1) и (2),
получим
(2)
Произведя соответствующие
преобразования в выражениях (1) и (2),
получим
![]() (3)
(3)
![]() (4)
откуда
(4)
откуда
![]() (5)
Решая уравнения (3) и (5), находим
(5)
Решая уравнения (3) и (5), находим
![]() (6)
(6)
![]() (7)
Разберем несколько примеров.
1. При ν2=0
(7)
Разберем несколько примеров.
1. При ν2=0
![]() (8)
(8)
![]() (9)
Проанализируем выражения (8) в
(9) для двух шаров различных масс:
а)
m1=m2.
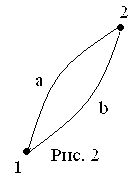
Если второй шар до удара висел неподвижно
(ν2=0)
(рис. 2), то после удара остановится первый
шар (ν1'=0),
а второй будет двигаться с той же
скоростью и в том же направлении, в
котором двигался первый шар до удара
(ν2'=ν1);
(9)
Проанализируем выражения (8) в
(9) для двух шаров различных масс:
а)
m1=m2.
Если второй шар до удара висел неподвижно
(ν2=0)
(рис. 2), то после удара остановится первый
шар (ν1'=0),
а второй будет двигаться с той же
скоростью и в том же направлении, в
котором двигался первый шар до удара
(ν2'=ν1);
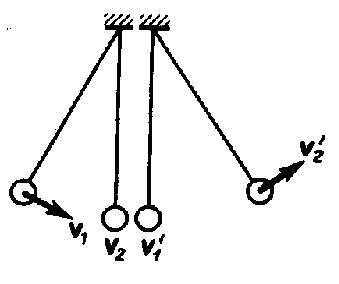
Рис.2
б) m1>m2. Первый шар продолжает двигаться в том же направлении, как и до удара, но с меньшей скоростью (ν1'<ν1). Скорость второго шара после удара больше, чем скорость первого после удара (ν2'>ν1' ) (рис. 3);
Рис.3
в) m1<m2. При ударе направление движения первого шара изменяется - шар отскакивает обратно. При этом второй шар движется в сторону, в которую двигался первый шар до удара, но с меньшей скоростью, т. е. ν2'<ν1 (рис. 4);
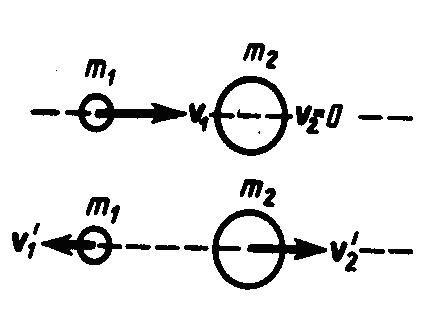
Рис.4
г) m2>>m1 (например, столкновение шара со стеной). Из уравнений (8) и (9) следует, что ν1'= -ν1; ν2' ≈ 2m1ν2'/m2. 2. При m1=m2 выражения (6) и (7) будут иметь вид ν1'= ν2; ν2'= ν1; т. е. шары равной массы как бы обмениваются скоростями. Абсолютно неупругий удар - соударение двух тел, в результате которого тела соединяются, двигаясь дальше как единое целое. Абсолютно неупругий удар можно продемонстрировать с помощью шаров из пластилина (глины), которые движутся навстречу друг другу (рис. 5).
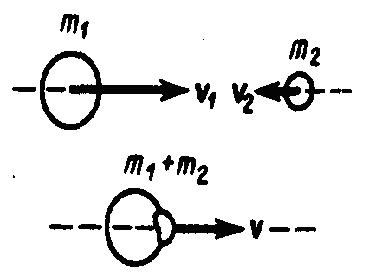
Рис.5
Если
массы шаров m1
и m2,
их скорости до удара ν1
и ν2,
то, используя закон сохранения импульса
![]()
 где
v
- скорость движения шаров после удара.
Тогда
где
v
- скорость движения шаров после удара.
Тогда
![]() (15.10)
В случае движения шаров навстречу
друг другу они вместе будут продолжать
движение в ту сторону, в которую двигался
шар с большим импульсом. В частном
случае, если массы шаров равны (m1=m2),
то
(15.10)
В случае движения шаров навстречу
друг другу они вместе будут продолжать
движение в ту сторону, в которую двигался
шар с большим импульсом. В частном
случае, если массы шаров равны (m1=m2),
то
![]() Определим,
как изменяется кинетическая энергия
шаров при центральном абсолютно неупругом
ударе. Так как в процессе соударения
шаров между ними действуют силы, зависящие
от их скоростей, а не от самих деформаций,
то мы имеем дело с дисипативными силами,
подобным силам трения, поэтому закон
сохранения механической энергии в этом
случае не должен соблюдаться. Вследствие
деформации происходит уменьшение
кинетической энергии, которая переходит
в тепловую или другие формы энергии.
Это уменьшение можно определить по
разности кинетической энергии тел до
и после удара:
Определим,
как изменяется кинетическая энергия
шаров при центральном абсолютно неупругом
ударе. Так как в процессе соударения
шаров между ними действуют силы, зависящие
от их скоростей, а не от самих деформаций,
то мы имеем дело с дисипативными силами,
подобным силам трения, поэтому закон
сохранения механической энергии в этом
случае не должен соблюдаться. Вследствие
деформации происходит уменьшение
кинетической энергии, которая переходит
в тепловую или другие формы энергии.
Это уменьшение можно определить по
разности кинетической энергии тел до
и после удара:
![]() Используя
(10), получаем
Используя
(10), получаем
![]() Если
ударяемое тело было первоначально
неподвижно (ν2=0),
то
Если
ударяемое тело было первоначально
неподвижно (ν2=0),
то
![]() и
и
![]() Когда
m2>>m1
(масса неподвижного тела очень велика),
то ν<<ν1
и практически вся кинетическая энергия
тела переходит при ударе в другие формы
энергии. Поэтому, например, для получения
значительной деформации наковальня
должна быть значительно массивнее
молота. Наоборот, при забивании гвоздей
в стену масса молота должна быть гораздо
большей (m1>>m2),
тогда ν≈ν1
и почти вся энергия тратится на возможно
большее перемещение гвоздя, а не на
остаточную деформацию стены.
Абсолютно
неупругий удар - это пример потери
механической энергии под действием
диссипативных сил.
Когда
m2>>m1
(масса неподвижного тела очень велика),
то ν<<ν1
и практически вся кинетическая энергия
тела переходит при ударе в другие формы
энергии. Поэтому, например, для получения
значительной деформации наковальня
должна быть значительно массивнее
молота. Наоборот, при забивании гвоздей
в стену масса молота должна быть гораздо
большей (m1>>m2),
тогда ν≈ν1
и почти вся энергия тратится на возможно
большее перемещение гвоздя, а не на
остаточную деформацию стены.
Абсолютно
неупругий удар - это пример потери
механической энергии под действием
диссипативных сил.
14
1. Работа переменной силы. Рассмотрим материальную точку, движущуюся под действием силы Р по прямой. Если действующая сила постоянна и направлена вдоль прямой, а перемещение равно s, то, как известно из физики, работа А этой силы равна произведению Ps. Теперь выведем формулу для подсчета работы, совершаемой переменной силой.
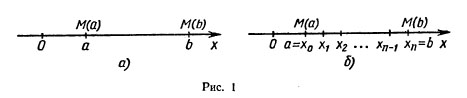
Пусть точка движется по оси Ох под действием силы, проекция которой на ось Ох есть функция f от х. При этом мы будем предполагать, что f есть непрерывная функция. Под действием этой силы материальная точка переместилась из точки М (а) в точку М (b) (рис. 1, а). Покажем, что в этом случае работа А подсчитывается по формуле
![]()
 (1)
(1)
Разобьем
отрезок [а; b] на п отрезков одинаковой
длины
![]() .Это
отрезки [а; x1],
[x1;
x2],...,
[xn-1;b]
(рис. 1,6). Работа силы на всем отрезке [а;
b] равна сумме работ этой силы на полученных
отрезках. Так как f есть непрерывная
функция от x, при достаточно малом отрезке
[а; x1]
работа силы на этом отрезке приблизительно
равна f (а) (x1—а)
(мы пренебрегаем тем, что f на отрезке
меняется). Аналогично работа силы на
втором отрезке [x1;
x2]
приближенно равна f (x1)
(x2
— x1)
и т. д.; работа силы на n-ом отрезке
приближенно равна f (xn-1)(b
— xn-1).
Следовательно, работа силы на всем
отрезке [а; b] приближенно равна:
.Это
отрезки [а; x1],
[x1;
x2],...,
[xn-1;b]
(рис. 1,6). Работа силы на всем отрезке [а;
b] равна сумме работ этой силы на полученных
отрезках. Так как f есть непрерывная
функция от x, при достаточно малом отрезке
[а; x1]
работа силы на этом отрезке приблизительно
равна f (а) (x1—а)
(мы пренебрегаем тем, что f на отрезке
меняется). Аналогично работа силы на
втором отрезке [x1;
x2]
приближенно равна f (x1)
(x2
— x1)
и т. д.; работа силы на n-ом отрезке
приближенно равна f (xn-1)(b
— xn-1).
Следовательно, работа силы на всем
отрезке [а; b] приближенно равна:
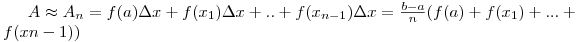
и точность приближенного равенства тем выше, чем короче отрезки, на которые разбит отрезок [а;b] Естественно, что это приближенное равенство переходит в точное, если считать, что n→∞:
![]()
Поскольку An при n →∞ стремится к интегралу рассматриваемой функции от а до b, формула (1) выведена. 2. Мощность.
Мощность P - это скорость совершения работы,
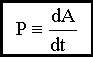
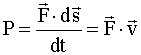 Здесь
v - скорость материальной точки, к которой
приложена сила
Здесь
v - скорость материальной точки, к которой
приложена сила
![]()
Все силы, встречающиеся в механике , принято разделять на консервативные и неконсервативные.
Сила, действующая
на материальную точку, называется
консервативной (потенциальной), если
работа этой силы зависит только от
начального и конечного положений точки.
Работа консервативной силы не зависит
ни от вида траектории, ни от закона
движения материальной точки по траектории
(см. рис. 2):
![]() .
.
Изменение направления
движения точки вдоль малого участка на
противоположное вызывает изменение
знака элементарной работы
![]() ,
следовательно,
,
следовательно,
![]() .
Поэтому работа консервативной силы
вдоль замкнутой траектории 1a2b1
равна нулю:
.
Поэтому работа консервативной силы
вдоль замкнутой траектории 1a2b1
равна нулю:
![]() .
.
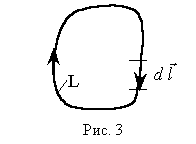
Точки 1и 2, а также участки замкнутой траектории 1a2 и 2b1 можно выбирать совершенно произвольно. Таким образом, работа консервативной силы по произвольной замкнутой траектории L точки ее приложения равна нулю:
![]() или
или
![]() .
(5)
.
(5)
В этой формуле
кружок на знаке интеграла показывает,
что интегрирование производится по
замкнутой траектории. Часто замкнутую
траекторию L
называют замкнутым контуром L
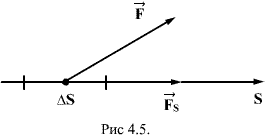
(рис. 3). Обычно задаются направлением
обхода контура L
по ходу часовой стрелки. Направление
элементарного вектора перемещения
![]() совпадает
с направлением обхода контура L.
В этом случае формула (5) утверждает:
циркуляция
вектора
совпадает
с направлением обхода контура L.
В этом случае формула (5) утверждает:
циркуляция
вектора
![]() по
замкнутому контуру L равна нулю.
по
замкнутому контуру L равна нулю.
Следует отметить, что силы тяготения и упругости являются консервативными, а силы трения неконсервативными. В самом деле, поскольку сила трения направлена в сторону, противоположную перемещению или скорости, то работа сил трения по замкнутому пути всегда отрицательна и, следовательно, не равна нулю.
Диссипативная система (или диссипативная структура, от лат. dissipatio — «рассеиваю, разрушаю») — это открытая система, которая оперирует вдали от термодинамического равновесия. Иными словами, это устойчивое состояние, возникающее в неравновесной среде при условии диссипации (рассеивания) энергии, которая поступает извне. Диссипативная система иногда называется ещё стационарной открытой системой или неравновесной открытой системой.
Диссипативная система характеризуется спонтанным появлением сложной, зачастую хаотичной структуры. Отличительная особенность таких систем — несохранение объёма в фазовом пространстве, то есть невыполнение Теоремы Лиувилля.
Простым примером такой системы являются ячейки Бенара. В качестве более сложных примеров называются лазеры, реакция Белоусова — Жаботинского и биологическая жизнь.
Термин «диссипативная структура» введен Ильёй Пригожиным.
Последние исследования в области «диссипативных структур» позволяют делать вывод о том, что процесс «самоорганизации» происходит гораздо быстрее при наличии в системе внешних и внутренних «шумов». Таким образом, шумовые эффекты приводят к ускорению процесса «самоорганизации».
15
Кинетическая энергия
энергия механической системы, зависящая от скоростей движения её точек. К. э. Т материальной точки измеряется половиной произведения массы m этой точки на квадрат её скорости υ, т. е. Т = 1/2 mυ2. К. э. механической системы равна арифметической сумме К. э. всех её точек: Т = Σ1/2 mkυ2k. Выражение К. э. системы можно ещё представить в виде Т = 1/2 Mυc2 + Tc, где М — масса всей системы, υc — скорость центра масс, Tc — К. э. системы в её движении вокруг центра масс. К. э. твёрдого тела, движущегося поступательно, вычисляется так же, как К. э. точки, имеющей массу, равную массе всего тела. Формулы для вычисления К. э. тела, вращающегося вокруг неподвижной оси, см. в ст. Вращательное движение.
Изменение К. э.
системы при её перемещении из положения
(конфигурации) 1
в положение 2
происходит под действием приложенных
к системе внешних и внутренних сил и
равно сумме работ
![]()
![]()
![]() .
Это равенство
выражает теорему об изменении К. э., с
помощью которой решаются многие задачи
динамики.
.
Это равенство
выражает теорему об изменении К. э., с
помощью которой решаются многие задачи
динамики.
При скоростях, близких к скорости света, К. э. материальной точки
![]()
,
где m0 — масса покоящейся точки, с — скорость света в вакууме (m0с2 — энергия покоящейся точки). При малых скоростях (υ<< c) последнее соотношение переходит в обычную формулу 1/2 mυ2.
Кинетическая энергия.
Кинетическая энергия - энергия движущегося тела.(От греческого слова kinema - движение). По определению кинетическая энергия покоящегося в данной системе отсчета тела обращается в ноль.
Пусть тело движется
под действием постоянной
силы
![]() в
направлении действия силы.
в
направлении действия силы.
Тогда:
![]() .
.
Т.к.
![]() .
.
Т.к. движение
равноускоренное, то:
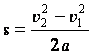 .
.
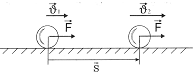
Следовательно:
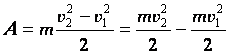 .
.
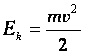
- кинетической энергией называется
величина, равная половине произведения массы тела на квадрат его скорости.
[Ek]=Дж.
Кинетическая энергия - величина относительная, зависящая от выбора СО, т.к. скорость тела зависит от выбора СО.
Т.о.
![]()
- эта формула выражает теорему о кинетической энергии: изменение кинетической энергии тела (материальной точки)за некоторый промежуток времени равно работе, совершенной силой, действующей на тело, за этот же промежуток времени
Эта теорема справедлива для любого движения и для сил любой природы. Если тело разгоняется из состояния покоя, то Ek1=0. Тогда A = Ek2. Следовательно, кинетическая энергия численно равна работе, которую необходимо совершить, чтобы разогнать тело из состояния покоя до данной скорости.
Вывод: Работа силы равна изменению кинетической энергии тела, т.е. A = Ek. Причем, A>0, если Ek увеличивается, и А<0, если Ek<0.
A = Ek
16
Потенциальная
энергия
![]() —
скалярная
физическая
величина,
характеризующая способность некоего
тела (или материальной точки) совершать
работу
за счет его нахождения в поле действия
сил. Другое определение: потенциальная
энергия — это функция координат,
являющаяся слагаемым в лагранжиане
системы, и описывающая взаимодействие
элементов системы[1].
Термин «потенциальная энергия» был
введен в XIX веке шотландским
инженером и физиком Уильямом
Ренкином.
—
скалярная
физическая
величина,
характеризующая способность некоего
тела (или материальной точки) совершать
работу
за счет его нахождения в поле действия
сил. Другое определение: потенциальная
энергия — это функция координат,
являющаяся слагаемым в лагранжиане
системы, и описывающая взаимодействие
элементов системы[1].
Термин «потенциальная энергия» был
введен в XIX веке шотландским
инженером и физиком Уильямом
Ренкином.
Единицей измерения энергии в СИ является Джоуль.
Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии.
Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными.
Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля.
Любая физическая система стремится к состоянию с наименьшей потенциальной энергией.
Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела.
Потенциальная энергия в поле тяготения Земли вблизи поверхности приближённо выражается формулой:
Ep = mgh,
где Ep — потенциальная энергия тела, m — масса тела, g — ускорение свободного падения, h — высота положения центра масс тела над произвольно выбранным нулевым уровнем.
Каждой точке
потенциального поля соответствует, с
одной стороны, некоторое значение
вектора силы
![]() ,
действующей на тело, и, с другой стороны,
некоторое значение потенциальной
энергии
,
действующей на тело, и, с другой стороны,
некоторое значение потенциальной
энергии
![]() .
Следовательно, между силой и потенциальной
энергией должна существовать определенная
связь.
.
Следовательно, между силой и потенциальной
энергией должна существовать определенная
связь.
Для установления
этой связи вычислим элементарную работу
![]() ,
совершаемую силами поля при малом
перемещении
,
совершаемую силами поля при малом
перемещении
![]() тела,
происходящем вдоль произвольно выбранного
направления в пространстве, которое
обозначим буквой
тела,
происходящем вдоль произвольно выбранного
направления в пространстве, которое
обозначим буквой
![]() .
Эта работа равна
.
Эта работа равна
![]()
где
![]() -
проекция силы
на
направление
.
-
проекция силы
на
направление
.
Поскольку в данном
случае работа совершается за счет запаса
потенциальной энергии
,
она равна убыли потенциальной энергии
![]() на
отрезке оси
:
на
отрезке оси
:
![]()
Из двух последних выражений получаем
![]()
Откуда
![]()
Последнее выражение дает среднее значение на отрезке . Чтобы
получить значение в точке нужно произвести предельный переход:
![]()
Так как может изменяться не только при перемещении вдоль оси , но также и при перемещениях вдоль других направлений, предел в этой формул представляет робой так называемую частную производную от по :
![]()
Это соотношение справедливо для любого направления в пространстве, в частности и для направлений декартовых координатных осей х, у, z:
![]()
Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы:
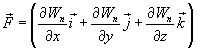
в математике вектор
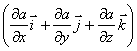 ,
,
где а - скалярная
функция х, у, z, называется градиентом
этого скаляра обозначается символом
![]() .
Следовательно сила равна градиенту
потенциальной энергии, взятого с обратным
знаком
.
Следовательно сила равна градиенту
потенциальной энергии, взятого с обратным
знаком
|
17
Полная механическая энергия системы – сумма ее кинетической и потенциальной энергии.
W=Wk+Wп=const (3.25)
Формула (3.25) выражает закон сохранения энергии в замкнутой системе, в которой действуют только консервативные силы: полная механическая энергия замкнутой системы тел, взаимодействующих между собой только консервативными силами, при любых движениях этих тел не изменяется. Происходят лишь взаимные превращения потенциальной энергии тел в их кинетическую энергию и обратно.
Системы, в которых полная механическая энергия сохраняется, называют консервативными.
Для полной механической энергии закон сохранения энергии имеет следующее выражение: полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения и упругости, остается неизменной.
18
Вращением твердого тела вокруг неподвижной оси называется такое движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, перпендикулярной плоскостям этих окружностей. Сама эта прямая есть ось вращения (рис. а).
Примером такого движения может послужить: вращение колес, валов двигателей и т.д.
Угловая скорость. Каждая точка вращающегося тела движется по окружности и различные точки проходят за время Δt разные пути. Так дуга АА1 больше дуги ВВ1, поэтому модуль скорости точки А больше, чем точке В (рис. б). Но радиусы окружностей поворачиваются за время Δt на один и тот же угол φ. Этот угол отсчитывается между лучами, выходящими из одной точки оси и перпендикулярными ей:
Первый луч - ОХ - неподвижен в пространстве
Второй луч - ОА - тесно связан с телом.
Пусть тело вращается равномерно, т.е. за одинаковые промежутки времени поворачивается на одинаковые углы. Быстрота вращения тела определяется углом поворота любого луча, связанного с телом, за данный интервал времени; она характеризуется угловой скоростью. Например, если одно тело за каждую секунду поворачивается на угол π/2, а другое - на угол π/4, то мы говорим, что первое тело вращается быстрее второго.
Угловой скоростью при равномерном вращении называется величина, равная отношению угла поворота тела к промежутку времени, за который этот поворот совершен.
Угловая скорость обозначается буквой ω («омега»), по определению она равна: ω=φ/Δt. Угловая скорость выражается в радианах в секунду (рад/с). Напомним что 1 радиан = 57°.
Угловою скорость можно выразить через частоту вращения, т.е число полных оборотов за 1 с. Если тело делает ν («ню») оборотов за 1 с, то время одного оборота равно 1/ν. Это называется периодом вращения и обозначают буквой Т.
Полному обороту тела соответствует угол φ=2π. Поэтому получим формулу: ω=2π/Т или ω=2πν.
Связь между линейной и угловой скоростью. Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть ее отличие от угловой скорости.
При вращении твердого тела разные его точки имеют разные линейные скорости, но угловая скорость для всех точек одинакова.
Между линейной скоростью какой-либо точки вращающегося тела и угловой скорость существует связь.Точка, лежащая на окружности радиуса R, за один оборот пройдет путь 2πR. А так как, время одного оборота тела есть период Т, то модуль линейной скорости можно найти так: v=2πR/T=2πRν или v=ωR.
Отсюда видно, что , чем дальше расположена точка тела от оси вращения, тем больше ее линейная скорость.
Модуль ускорения точки, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности: a=v2/R, но v=ωR. Следовательно, a=ω2R.
Чем дальше расположена точка твердого тела от оси вращения, тем больше по модулю ускорение он имеет.
