2.2. Парная нелинейная регрессия

В данном разделе следует:

1. получить уравнение парной нелинейной квадратичной регрессии y=a+bx+cx²+ε;

2. оценить тесноту нелинейной связи переменных с помощью индекса корреляции ;

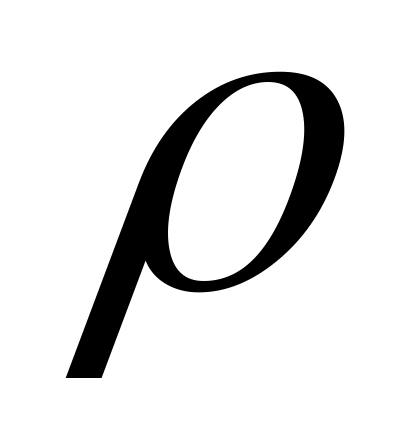3. оценить качество подгонки квадратичного уравнения коэффициентом детерминации R²;

4. оценить качество модели с помощью средней относительной ошибки аппроксимации ;

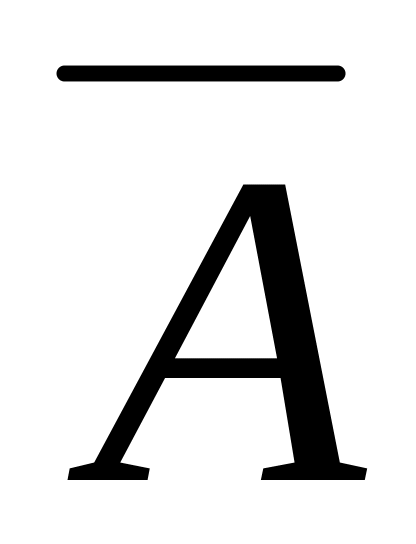5. аналогичные расчеты выполнить для:

• линейной модели y=a+bx+ε;

• гиперболической модели y=a+b/x+ε;

• степенной модели y=a·x^b·ε;

• показательной модели y=a·b^x·ε;

  6. результаты совместить на одном графике, сделать вывод какая из этих моделей предпочтительнее.

Оценка параметров параболы второй степени (квадратичной регрессии) при помощи МНК приводит к системе следующих нормальных уравнений:

Система линейных алгебраических уравнений (СЛАУ) в матричном виде выглядит следующими образом:

AX=B

где:

, ,

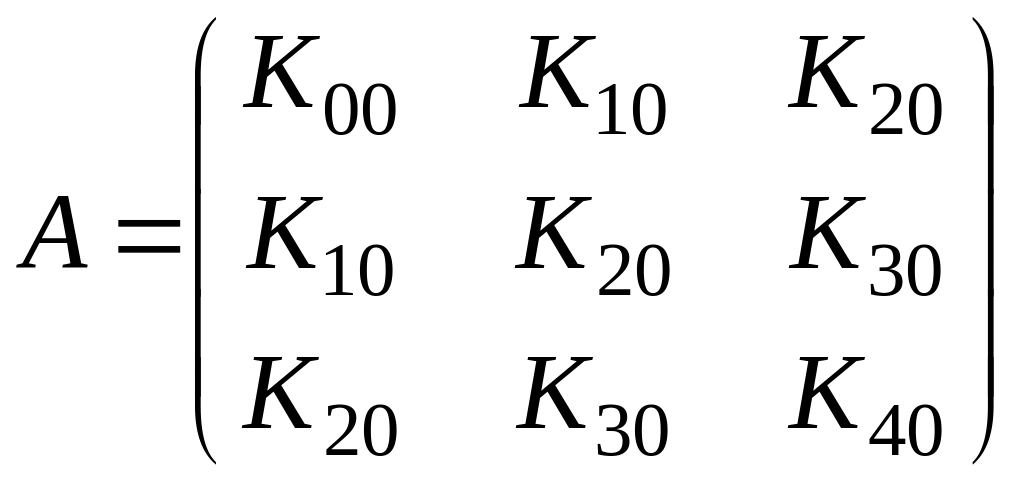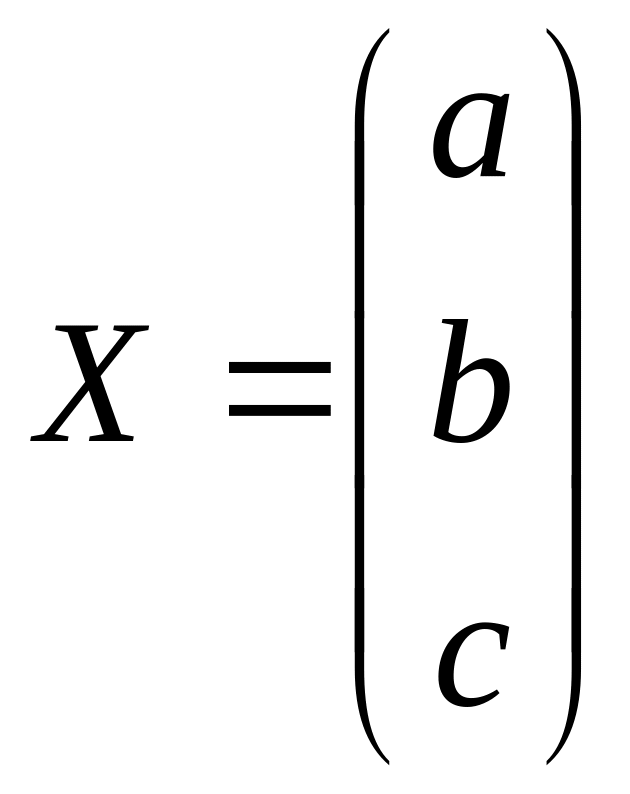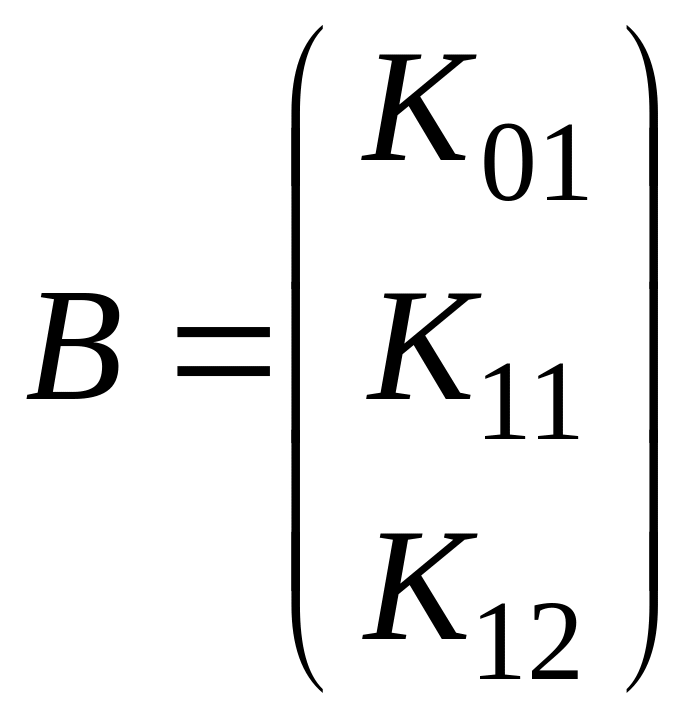
Для удобства обозначим коэффициенты уравнения следующим образом: K₀₀=n, K₁₀=Σx, K₂₀= Σx², K₃₀= Σx³, K₄₀= Σx⁴, K₀₁=Σy, K₁₁=Σyx, K₁₂=Σyx².

Алгоритм метода Крамера для системы уравнений состоящей из трех неизвестных заключается в следующем: вычисляем определитель основной матрицы системы дельта - Δ, если он не равен нулю, значит система совместна, то есть имеет решение, и тогда находим определитель Δ₁, который отличается от первого тем, что первый столбец заменяем столбцом свободных коэффициентов, аналогично определяются остальные определители Δ₂ и Δ₃.

В результате подстановки, матрица главного определителя системы будет выглядеть:

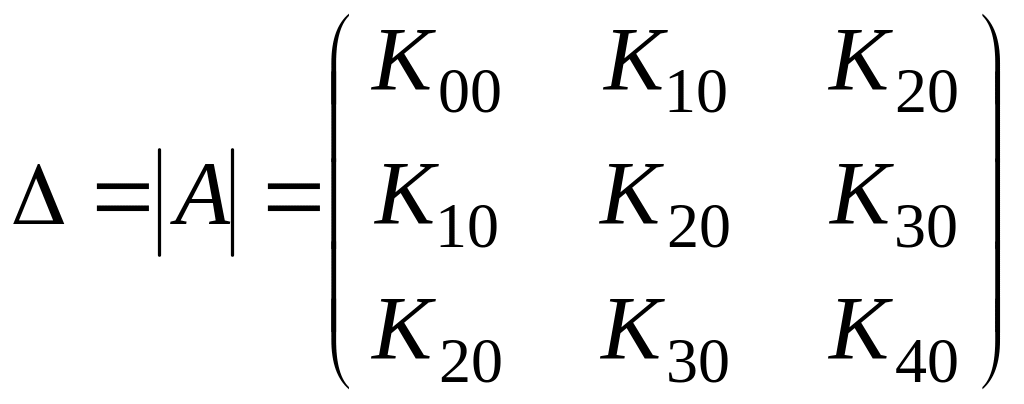
Соответственно матрицы первого, второго и третьего определителей:

, ,

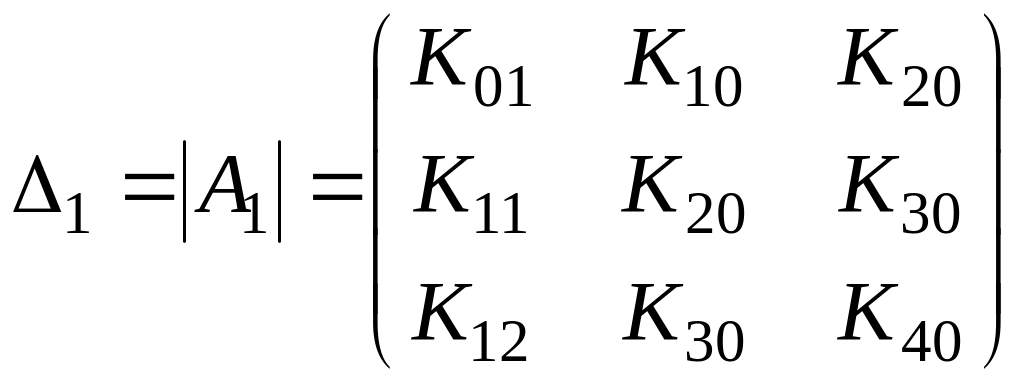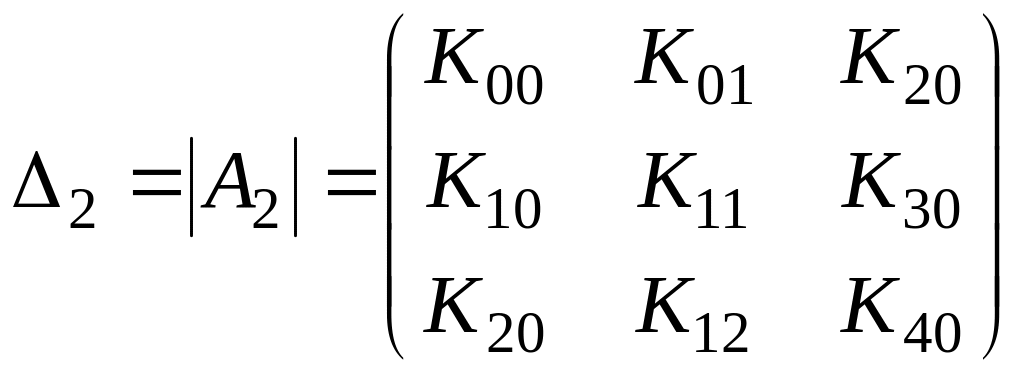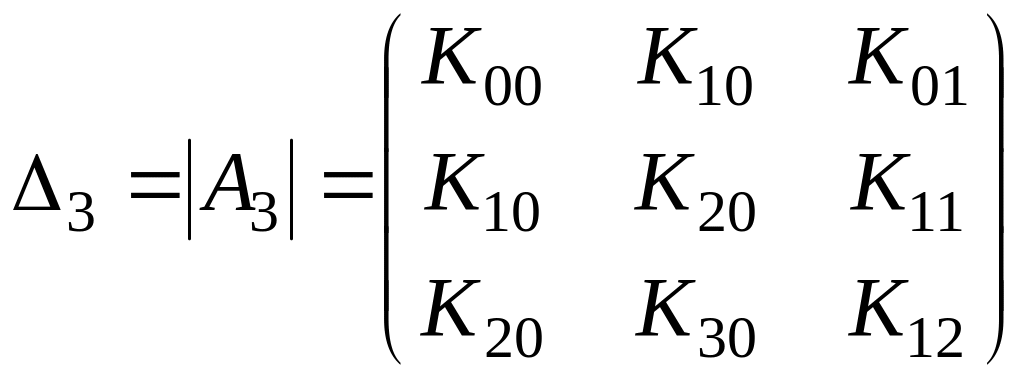
Неизвестные параметры системы определяются следующим образом:

, ,

Для оценки тесноты нелинейной связи переменных используют индекс корреляции:

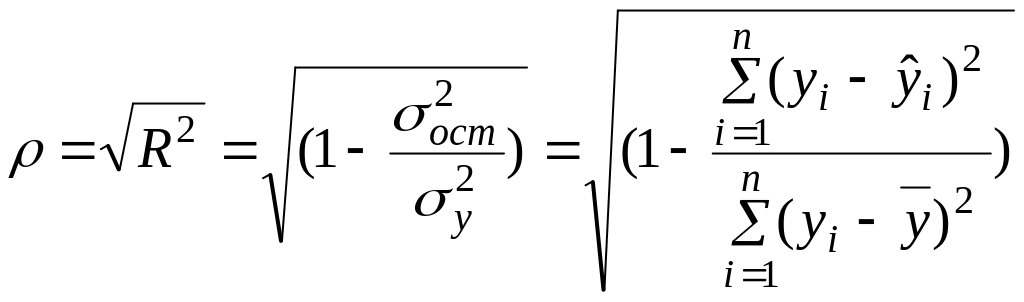
Коэффициент детерминации R² и средняя относительная ошибка характеризуют качество не только линейного, но и нелинейного уравнения регрессии. Силу связи переменных в нелинейной (как и в линейной) регрессии характеризует средний коэффициент эластичности .

Особенностью модели вида y=a+b/x+ε (гипербола) является то, что она нелинейная по объясняющей переменной.

Гипербола приводится к линейному уравнению заменой: z=1/x, тогда уравнение примет вид: y=a+bz+ε.

Система линейных уравнений при применении МНК будет выглядеть следующим образом:

Модель y=a·x^b·ε (степенная) нелинейна относительно оцениваемых параметров, однако ее можно считать внутренне линейной, т.к. логарифмирование данного уравнения по основанию е приводит его к линейному виду:

Обозначим Y=ln(y), A=ln(a), X=ln(x), E=ln(ε).

Вместо исходного нелинейного степенного уравнения получим уравнение Y=A+bX+E, линейное относительно вновь введенных переменных.

Модель y=a·b^x·ε (показательная) также нелинейна по объясняемым переменным и может быть сведена к линейной. Линеаризация аналогична проведенному выше преобразованию.

Прологарифмируем обе части уравнения регрессии:

ln((y)=ln(a)+x·ln(b)+ln(ε)

Введем промежуточные переменные Y=ln(y), A=ln(a), B=ln(b), E=ln(ε), тогда уравнение примет вид: Y=A+x·B+E.