2 Получение математической модели системы управления

Система управления может быть представлена приблизительно структурной схемой, изображенной на рисунке 2.1.

Рисунок 2.1 – Структурная схема исследуемой системы стабилизации

2.1 Идентификация модели объекта управления

В качестве объекта управления рассматривается измеритель-регулятор ТРМ-10. Весьма распространенным в практике методом идентификации промышленных объектов управления является скачкообразное изменение величины на входе (в режиме установившегося сигнала на выходе) и регистрация соответствующей реакции на выходе. Если пренебречь длительностью скачка и его величину принять за единицу, то изменение выходной величины по отношению к изменению величины на входе будет представлять переходную характеристику объекта.

При таком экспериментальном исследовании переходная характеристика (кривая разгона) часто наблюдается как апериодический (монотонный) процесс с точкой перегиба или как колебательный монотонно затухающий процесс и в обоих случаях выходная величина явно стремится к новому постоянному значению. В таких случаях часто пытаются идентифицировать объект управления как объект 2-го и выше порядков, вычисляя тем или иным способом коэффициенты дифференциального уравнения (или передаточной функции) по экспериментальной переходной характеристике.

Для получения кривой разгона объекта управления, ТРМ-10 нагревали до 80 градусов Цельсия и каждые 30 секунд снимали показания с термопары и с рассогласования температуры, преобразованного в вольты. Полученные данные являются реакцией системы на единичный скачок. По полученной характеристике требуется произвести идентификацию объекта.

2.1.1 Предварительная обработка экспериментальных данных

Полученные экспериментально две переходные характеристики представлены на рисунке 2.2.

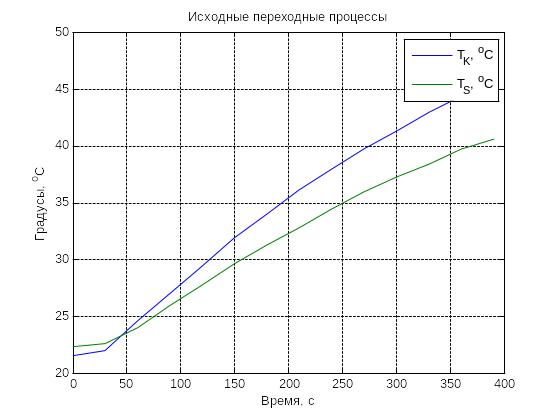
Рисунок 2.2 – Экспериментальная переходная характеристика

Полученные данные необходимо нормировать и усреднить, используя следующее соотношение:

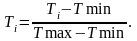
Полученный усредненный процесс представлен на рисунке 2.3.

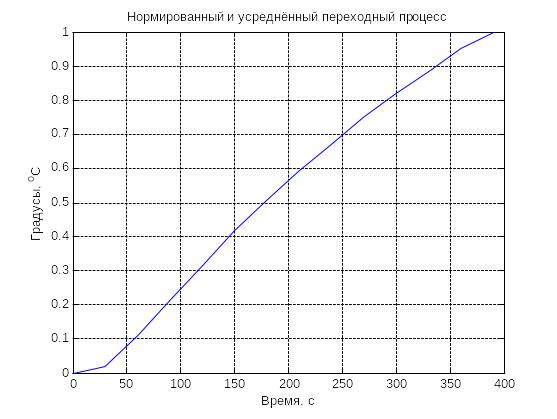
Рисунок 2.3 – Нормированный и усредненный переходный процесс

Структура аппроксимирующего выражения для передаточной функции объекта может быть выбрана в общем случае в виде:

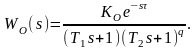
Коэффициент усиления объекта управления 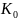можно найти по графику переходного процесса. Постоянные времени передаточной функции могут быть найдены методом площадей, геометрическим и методом Ротача.

2.1.2 Определение коэффициента усиления объекта управления

Для определения коэффициента усиления объекта управления воспользуемся статической характеристикой объекта управления (рисунок 2.4), построенной по экспериментальным данным.

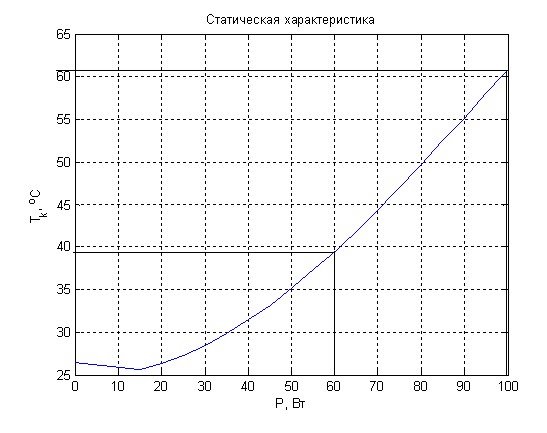
Рисунок 2.4 – Статическая характеристика объекта управления

Выделим на графике линейный участок. Коэффициент усиления объекта управления определим из соотношения:

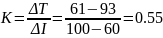
2.1.3 Аппроксимация объекта управления математической моделью 1-го порядка

Представим математическую модель объекта как апериодическое звено первого порядка с запаздыванием:

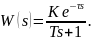
Коэффициент усиления для нормированного переходного процесса равен единице. Запаздыванием выберем равное 30 (это следует из рисунка 2.3). Постоянную времени найдем интегральным методом (удобно для автоматизации процесса нахождения постоянной времени в прикладных программах):

Более точно постоянную времени можно найти интегральным методом (это удобно для автоматизации процесса нахождения постоянной времени в прикладных программах):

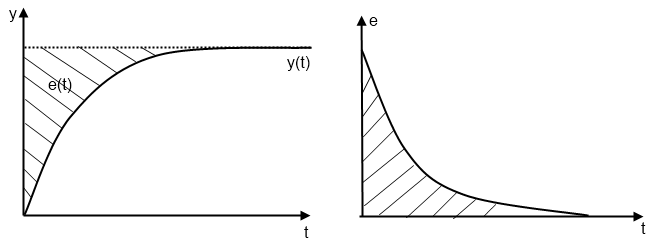
Отсюда нетрудно заметить, что можно найти из соотношения:

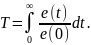
В нашем случае T= 187.5092.

Полученный переходный процесс для данной модели показан на рисунке 2.5. Реализация метода для нахождения постоянной времени приведена в приложении А. Для данного случая найдена передаточная функция следующего вида:

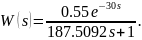
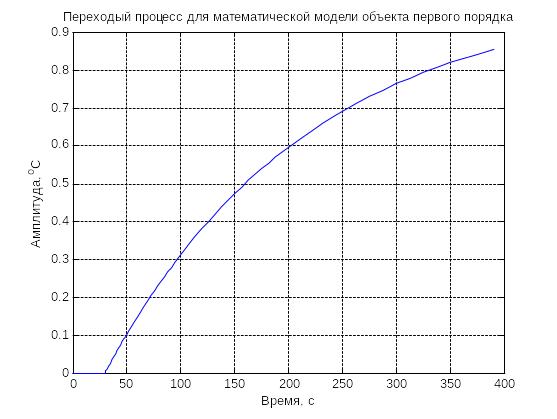
Рисунок 2.5 – Переходный процесс для математической модели объекта первого порядка

2.1.4 Аппроксимация объекта управления математической моделью 2-го порядка

Представим математическую модель объекта как апериодическое звено второго порядка без запаздывания с помощью метода, предложенного в [1], в литературе используется понятие метод Ротача в частном случае. Способ предполагает отыскание точки перегиба на экспериментальной кривой и проведение через нее касательной до пересечения с горизонтальной осью координат (ось времени) и с асимптотой, к которой стремится переходная функция.

Передаточная функция ищется в виде:

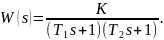
Для метода необходимо считать с графика отрезки T_a и T_b , как показано на рисунке 2.6.

Таким образом, по двум интервалам, полученным по экспериментальным данным, необходимо найти две постоянные времени T₁ и T₂.

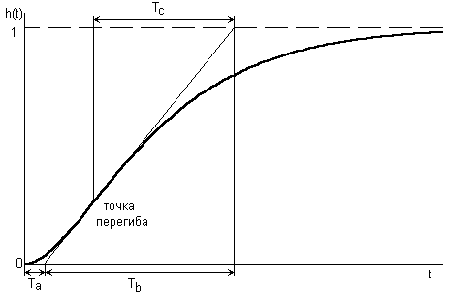
Рисунок 2.6 – Измеряемые отрезки на экспериментальной переходной функции

Реализация метода для нахождения двух постоянные времени T₁ и T₂ приведена в приложении А.

В результате получены значения отрезков T_a=30 и T_b=313. После определения отрезков методом половинного деления решаются уравнения, и потом происходит вычисление постоянных времени. Для данного случая они T₁= 76.5135 и T₂=158.6992. Переходный процесс для полученной модели приведен на рисунке 2.7.

Для данного случая найдена передаточная функция следующего вида:

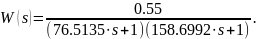
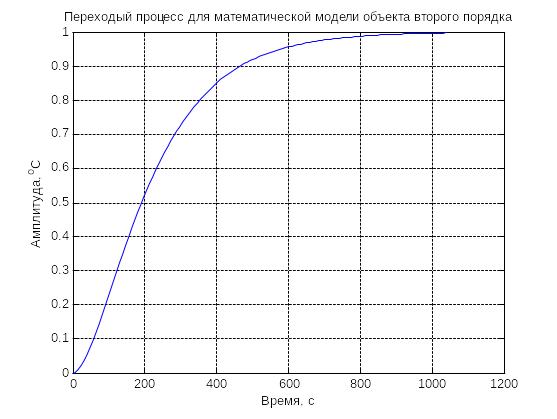
Рисунок 2.7 – Переходный процесс для математической модели объекта второго порядка

2.1.5 Аппроксимация объекта управления математической моделью 3-го порядка

Когда экспериментальная информация представлена в виде переходной характеристики и неизвестно, какой порядок имеет система, возникают определенные трудности. Одним из возможных методов ее решения является метод, известный под названием метода площадей [2, 3]. Модель, получаемая методом площадей, в общем случае даёт лучшее описание реальной системы, так как она строится при произвольном расположении полюсов.

Передаточная функция ищется в виде:

Таким образом, задача определения W(s) по известной h(t) состоит в отыскании способа вычисления коэффициентов A1, A2, A3, ...

Связь между h(t) и W(s) задается известным выражением:

.

Рассмотрим выражение:

С другой стороны, по определению преобразования Лапласа:

Обозначим [1 - h(t)/K] = x и применим разложение

Тогда

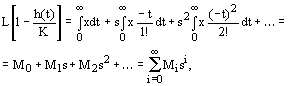
где

Следовательно, получим тождество:

,

Умножая знаменатель левой части на правую часть и приравнивая коэффициенты при равных степенях s, получим:

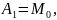
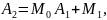
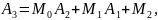
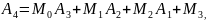
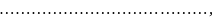
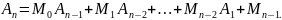
Подставим в последнюю формулу M_i:

.

Таким образом, последовательно можно вычислить:

,

,

,

,

,

.

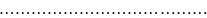Реализация данного метода приведена в приложении А. Для данного случая найдена передаточная функция следующего вида:

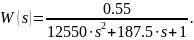
Переходный процесс представлен на рисунке 2.8.

Рисунок 2.8 – Переходный процесс для математической модели объекта третьего порядка

2.1.6 Сравнительный анализ полученных математических моделей объекта

В предыдущих пунктах получены конкурирующие математические модели при помощи различных методов идентификации. Необходимо проанализировать полученные модели, чтоб выбрать модель, которая наиболее точней аппроксимирует объект управления по полученным экспериментальным данным, для этого как критерий отбора используем функцию потерь:

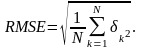
Здесь 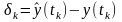– рассогласование между измеренным экспериментально выходом 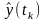и выходом 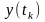системы в момент времени t_k, полученного в результате моделирования , где N – объём выборки измерений выхода системы.

Сводная характеристика представлена в приведенной ниже таблице 2.1.

Таблица 2.1 – Сводная характеристика оценок конкурирующих моделей

Порядок модели	Метод расчета	RSME
Первый	интегральный	23.7913
Второй	метод Ротача	0.0768
Третий	метод площадей	0.0242

Как видно из приведенных значений оценок, математическая модель, полученная с помощью метода площадей, наилучшим образом аппроксимирует экспериментальные данные и можно принять её за эталонную модель исследуемого объекта. То есть передаточная функция объекта управления будет иметь вид:

Экспериментальные данные и данные, полученные в результате моделирования, приведены на рисунке 2.9.

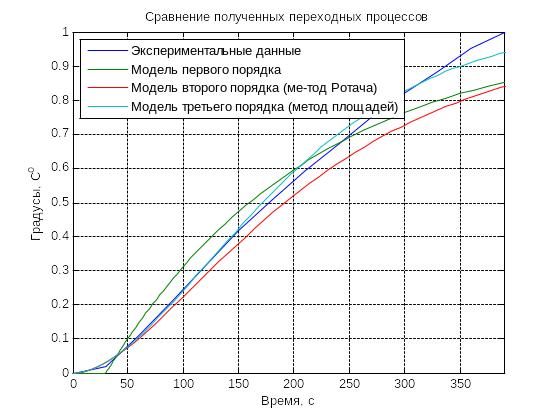
Рисунок 2.9 – Сравнительная характеристика качества аппроксимации