
Неориентированные графы
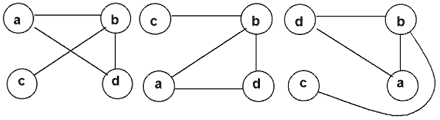
Граф - это двойка <V, E>, где V - непустое множество вершин, а Е - множество ребер, соединяющих эти вершины попарно (иначе говоря, ребро --- это пара вершин). Если две вершины, связанные между собой ребром, равноправны, то графы называются неориентированными: нет никакой разницы между "началом" и "концом" ребра.
Ориентированные графы
Орграф - это граф, все ребра которого имеют направление. Такие направленные ребра называются дугами. На рисунках дуги изображаются стрелочками.
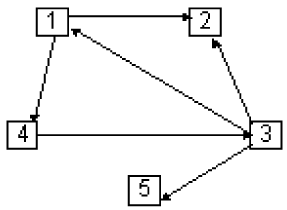
В отличие от ребер, дуги соединяют две неравноправные вершины: одна из них называется началом дуги ( дуга из нее исходит ), вторая - концом дуги ( дуга в неё входит ). Можно сказать, что любое ребро - это пара дуг, направленных навстречу друг другу.
Способы представления графов:
Первый способ: массив ребер.
Пусть в графе M ребер. Заведем массив размером Mx2, в котором будем хранить ребра парами вершин, которые они соединяют. Это наиболее понятный, но достаточно неудобный способ хранения графа. Однако у него есть один большой плюс - при таком способе представления легко вводить дополнительные характеристики ребер. Например, чтобы сохранить веса ребер, достаточно сделать массив размером Mx3 и в дополнительную ячейку для каждого ребра записать его вес.
Второй способ: матрица смежности.
Матрица смежности Sm - это квадратная матрица размером NxN ( N - количество вершин в графе ), заполненная единицами и нулями по следующему правилу:
Если в графе имеется ребро e, соединяющее вершины u и v, то Sm[u,v] = 1, в противном случае Sm[u,v] = 0. Аналогично, если граф имеет кратные ребра, то в элемент Sm[u,v] запишем количество ребер из вершины u в вершину v.
Заметим, что данное определение подходит как ориентированным, так и неориентированным графам: матрица смежности для неориентированного графа будет симметричной относительно своей главной диагонали, а для орграфа - несимметричной.
Задать взвешенный граф при помощи матрицы смежности тоже возможно. Необходимо лишь внести небольшое изменение в определение:
Если в графе имеется ребро e, соединяющее вершины u и v, то Sm[u,v] = ves(e), в противном случае Sm[u,v] = 0.
В матрице смежности графа без петель на главной диагонали стоят 0.
Третий способ: списки смежности.
Этот способ задания графов подразумевает, что для каждой вершины будет указан список всех смежных с нею вершин (для орграфа - список вершин, являющихся концами исходящих дуг ). Наиболее естественно применять этот способ для задания орграфов, однако и для остальных вариантов он тоже подходит.
УКАЗАНИЕ: Для работы со списками в DELPHI используйте указатели или класс TLIST. В С++ используйте указатели или класс VECTOR.
ПРИМЕР. Задать граф списками смежности. Вывести на экран.
program Graph1;
{$APPTYPE CONSOLE}
uses
SysUtils,
classes;
const n=5;
var i,j:integer; v:array[1..n] of TList; p:^integer;
begin
for I := 1 to n do
begin
v[i]:=TList.Create;//создаем объект класса TList(список)
writeln(I, ':');
while not eoln do//заполняем список смежности для вер. i
begin
new(p);
read(p^);
v[i].Add(p);
end;
readln;
end;
for I := 1 to n do
begin
for j := 0 to v[i].Count-1 do
write((integer(v[i].Items[j]^)),' ');
writeln;
end;
readln;
end.
ЗАДАЧИ.
1. По матрице смежности построить списки смежности неориентированного графа и подсчитать степени его вершин.
2. По массиву рёбер построить списки смежности ориентированного графа и подсчитать полустепени исхода его вершин.
3. По матрице смежности построить списки смежности ориентированного графа и подсчитать полустепени захода его вершин.
4. По массиву рёбер построить списки смежности неориентированного графа и подсчитать степени его вершин.
5. По массиву рёбер построить списки смежности неориентированного графа, записи в каждом списке упорядочить по убыванию номеров вершин.
7. По матрице смежности построить списки смежности ориентированного графа, записи в каждом списке упорядочить по убыванию номеров вершин.
9. По матрице смежности построить списки смежности неориентированного графа, удалить из графа все рёбра, начинающиеся и заканчивающиеся в вершинах n1, n2, n3.
10. По таблице рёбер ориентированного графа построить списки смежности, добавить рёбра с началом в вершинах с номерами, кратными 2, и концом в вершинах с номерами, кратными 3.
11. По массиву рёбер ориентированного графа построить списки смежности, удалить из графа вершины с номерами n1 и n2.
12. По массиву рёбер ориентированного графа построить списки смежности, удалить из графа рёбра, оканчивающиеся в вершинах n1 и n2.
12. По матрице смежности ориентированного графа построить списки смежности, добавить рёбра с началом в вершинах n1, n2 и концом в вершинах n3, n4.
13. По массиву рёбер неориентированного графа построить списки смежности, удалить из графа все рёбра, обе вершины которых кратны 3.
14. По массиву рёбер ориентированного графа построить списки смежности и найти все вершины, которые являются его истоками, и все его вершины, которые являются его стоками.
15. По массиву рёбер ориентированного графа построить списки смежности, записи в каждом списке упорядочить по возрастанию номеров вершин.
16. По матрице смежности неориентированного графа построить списки смежности, записи в каждом списке упорядочить по возрастанию номеров вершин.
17. По массиву рёбер неориентированного графа построить матрицу смежности. Проверить, что заданный неориентированный граф является транзитивным. Граф называется транзитивным, если всегда из того, что вершины u и v соединены ребром и вершины v и w соединены ребром следует, что вершины u и w соединены ребром.
18. Ориентированный граф называется турниром, если между любой парой его различных вершин существует ровно одно ребро. Для заданного списком ребер графа проверьте, является ли он турниром.
19. Ориентированный граф называется полуполным, если между любой парой его различных вершин есть хотя бы одно ребро. Для заданного списком ребер графа проверьте, является ли он полуполным. По списку
20. Неориентированный граф называется полным, если любая пара его различных вершин соединена хотя бы одним ребром. Для заданного списком ребер графа проверьте, является ли он полным.
21. Неориентированный граф называется регулярным, если все его вершины имеют одинаковую степень. Для заданного списком ребер графа проверьте, является ли он регулярным.
22. Напомним, что вершина ориентированного графа называется истоком, если в нее не входит ни одно ребро и стоком, если из нее не выходит ни одного ребра. Ориентированный граф задан матрицей смежности. Найдите все вершины графа, которые являются истоками, и все его вершины, которые являются стоками.
23. Ориентированный граф задан списком ребер. Найдите степени всех вершин графа.
24. Ориентированный граф задан матрицей смежности. Найдите полустепени захода и полустепени исхода всех вершин графа.
25. Простой неориентированный граф задан списком ребер, выведите его представление в виде матрицы смежности.
26. Ориентированный граф задан матрицей смежности, выведите его представление в виде списка ребер.
