
- •Раздел 7
- •1. Система координат на плоскости
- •1.1. Декартова система координат
- •Повторение некоторых сведений из раздела «Элементы векторной алгебры»
- •1.2. Преобразование системы координат
- •1. Параллельный перенос осей координат
- •2. Поворот осей координат
- •1.3. Полярная система координат
- •1.4. Линии на плоскости
- •2. Уравнение прямой на плоскости
- •2.1. Общее уравнение прямой
- •2.2. Уравнение прямой с угловым коэффициентом
- •2.3. Каноническое уравнение прямой
- •2.4. Параметрические уравнения прямой
- •2.5. Уравнение прямой, проходящей через две точки
- •2.6. Уравнение прямой в отрезках
- •2.7. Расположение двух прямых на плоскости
- •Условия параллельности двух прямых
- •Условия перпендикулярности двух прямых
- •Угол между двумя прямыми
- •2.8. Расстояние от точки до прямой
- •3. Линии второго порядка
- •3.1. Окружность
- •3.2. Эллипс
- •3.3. Гипербола
- •3.4. Парабола
- •4. Уравнения поверхности и
- •4.1. Системы координат в пространстве
- •1. Прямоугольные декартовы координаты в пространстве
- •2. Цилиндрические координаты
- •3. Сферические координаты
- •4.2. Уравнения поверхности и линии в пространстве
- •5. Уравнение плоскости
- •5.1. Общее уравнение плоскости
- •5.6. Расположение двух плоскостей Условия параллельности и перпендикулярности двух плоскостей
- •Угол между двумя плоскостями
- •5.7. Расстояние от точки до плоскости
- •6. Уравнение прямой
- •6.1. Канонические и параметрические уравнения прямой
- •6.2. Уравнение прямой, проходящей через две точки
- •6.3. Общие уравнения прямой в пространстве
- •6.4. Взаимное расположение двух прямых в пространстве
- •6.5. Угол между двумя прямыми
- •6.6. Расстояние от точки до прямой. Расстояние между двумя скрещивающимися прямыми
- •6.7. Взаимное расположение прямой и плоскости
- •Определение точки пересечения прямой и плоскости
- •Угол между прямой и плоскостью
- •7. Поверхности второго порядка
- •7.1. Канонические уравнения и поверхности второго порядка
3.4. Парабола
Определение 3.5. Параболой называется множество точек плоскости, равноудаленных от данной точки, называемой фокусом параболы, и данной прямой, называемой ее директрисой.
Расстояние от фокуса
![]() до директрисы называется фокальным
параметром параболы и обозначается
до директрисы называется фокальным
параметром параболы и обозначается
![]() .
.
Для вывода уравнения параболы выберем
систему координат
так, чтобы ось
прошла через фокус
перпендикулярно директрисе в направлении
от директрисы к
,
а начало координат
![]() расположим посередине между фокусом и
директрисой.
расположим посередине между фокусом и
директрисой.
В выбранной системе координат фокус
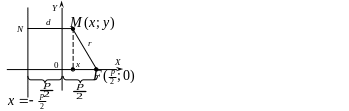
![]() ,
а уравнение директрисы имеет вид
,
а уравнение директрисы имеет вид
![]() .
Пусть
произвольная точка
параболы. Соединим точку
с
,
где
.
Пусть
произвольная точка
параболы. Соединим точку
с
,
где
![]() называется фокальным радиусом
точки
.
Проведем отрезок
называется фокальным радиусом
точки
.
Проведем отрезок
![]() перпендикулярно директрисе. Согласно
определению параболы
перпендикулярно директрисе. Согласно
определению параболы
![]() .
По формуле расстояния между двумя
точками находим:
.
По формуле расстояния между двумя
точками находим:
![]() ,
а
,
а
![]() .
.
Следовательно,
![]() .
.
Возведя обе части уравнения в квадрат, получим
![]() ,
,
т.е.
![]() .
(3.7)
.
(3.7)
Уравнение (3.7) называется каноническим уравнением параболы.
Для любой точки
параболы
![]() .
Так как для точек эллипса и гиперболы
.
Так как для точек эллипса и гиперболы
![]() ,
то для параболы естественно считать
эксцентриситет
,
то для параболы естественно считать
эксцентриситет
![]() .
.
Чтобы установить форму параболы и построить ее в прямоугольной системе координат , проведем исследование ее канонического уравнения.
1. В уравнении (3.7) переменная входит в четной степени, значит, парабола симметрична относительна оси ; ось является осью симметрии параболы.
2. Так как
![]() ,
то из (3.7) следует, что
,
то из (3.7) следует, что
![]() .
Следовательно, парабола расположена
справа от оси
.
.
Следовательно, парабола расположена
справа от оси
.

Уравнения вида
![]() ,
,
![]() и
и
![]() также определяют параболы, которые
изображены на рисунке.
также определяют параболы, которые
изображены на рисунке.
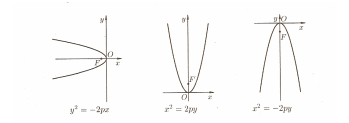
Нетрудно показать, что график квадратного
трехчлена
![]() ,
где
,
где
![]() ,
,
![]() и
любые действительные числа, представляет
собой параболу в смысле приведенного
выше ее определения.
и
любые действительные числа, представляет
собой параболу в смысле приведенного
выше ее определения.
Замечание. Если вершина
параболы
![]() или
смещена в точку
,
то ее каноническое уравнение имеет вид
или
смещена в точку
,
то ее каноническое уравнение имеет вид
![]() или
или
![]() .
.
Для параболы
![]() ,
осью симметрии служит прямая
,
осью симметрии служит прямая
![]() ,
а фокус имеет координаты
,
а фокус имеет координаты
![]() ,
директриса описывается уравнением
,
директриса описывается уравнением
![]() .
.
Аналогично для параболы
![]() ,
осью симметрии служит прямая
,
осью симметрии служит прямая
![]() ,
а фокус имеет координаты
,
а фокус имеет координаты
![]() ,
директриса описывается уравнением
,
директриса описывается уравнением
![]() .
.
Пример 3.3. Установить вид кривой второго порядка, заданной уравнением
![]() .
.
Решение. Выделим в этом уравнении полные квадраты:
![]()
![]()
![]()
 .
.
Данное уравнение определяет гиперболу
с центром в точке
![]() ;
действительная полуось
;
действительная полуось
![]() ,
мнимая полуось
,
мнимая полуось
![]() ;
эксцентриситет
;
эксцентриситет
 .
.
4. Уравнения поверхности и
ЛИНИИ В ПРОСТРАНСТВЕ
4.1. Системы координат в пространстве
1. Прямоугольные декартовы координаты в пространстве
Прямоугольная декартова система координат в пространстве определяется тремя пересекающимися в одной точке взаимно перпендикулярных осей, занумерованных в определенном порядке и масштаба (отрезка для измерения длин).
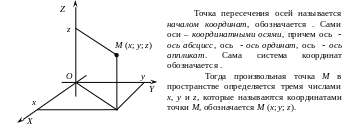
Прямоугольная система координат
![]() в пространстве позволяет установить
взаимно однозначное соответствие между
точками пространства и тройками чисел
x, y
и z
их координатами.
в пространстве позволяет установить
взаимно однозначное соответствие между
точками пространства и тройками чисел
x, y
и z
их координатами.
Каждая пара координатных осей определяет
координатную плоскость. Координатные
плоскости обозначают соответственно
,
![]() ,
,
![]() .
Эти координатные плоскости делят все
точки пространства, на принадлежащие
им, на восемь частей, называемых октантами.
.
Эти координатные плоскости делят все
точки пространства, на принадлежащие
им, на восемь частей, называемых октантами.
