
- •Раздел 7
- •1. Система координат на плоскости
- •1.1. Декартова система координат
- •Повторение некоторых сведений из раздела «Элементы векторной алгебры»
- •1.2. Преобразование системы координат
- •1. Параллельный перенос осей координат
- •2. Поворот осей координат
- •1.3. Полярная система координат
- •1.4. Линии на плоскости
- •2. Уравнение прямой на плоскости
- •2.1. Общее уравнение прямой
- •2.2. Уравнение прямой с угловым коэффициентом
- •2.3. Каноническое уравнение прямой
- •2.4. Параметрические уравнения прямой
- •2.5. Уравнение прямой, проходящей через две точки
- •2.6. Уравнение прямой в отрезках
- •2.7. Расположение двух прямых на плоскости
- •Условия параллельности двух прямых
- •Условия перпендикулярности двух прямых
- •Угол между двумя прямыми
- •2.8. Расстояние от точки до прямой
- •3. Линии второго порядка
- •3.1. Окружность
- •3.2. Эллипс
- •3.3. Гипербола
- •3.4. Парабола
- •4. Уравнения поверхности и
- •4.1. Системы координат в пространстве
- •1. Прямоугольные декартовы координаты в пространстве
- •2. Цилиндрические координаты
- •3. Сферические координаты
- •4.2. Уравнения поверхности и линии в пространстве
- •5. Уравнение плоскости
- •5.1. Общее уравнение плоскости
- •5.6. Расположение двух плоскостей Условия параллельности и перпендикулярности двух плоскостей
- •Угол между двумя плоскостями
- •5.7. Расстояние от точки до плоскости
- •6. Уравнение прямой
- •6.1. Канонические и параметрические уравнения прямой
- •6.2. Уравнение прямой, проходящей через две точки
- •6.3. Общие уравнения прямой в пространстве
- •6.4. Взаимное расположение двух прямых в пространстве
- •6.5. Угол между двумя прямыми
- •6.6. Расстояние от точки до прямой. Расстояние между двумя скрещивающимися прямыми
- •6.7. Взаимное расположение прямой и плоскости
- •Определение точки пересечения прямой и плоскости
- •Угол между прямой и плоскостью
- •7. Поверхности второго порядка
- •7.1. Канонические уравнения и поверхности второго порядка
5.6. Расположение двух плоскостей Условия параллельности и перпендикулярности двух плоскостей
Пусть две плоскости P1 и P2 заданы своими общими уравнениями:
![]() ;
;
![]() .
.
Если плоскости P1
и P2 параллельны,
то параллельны и их нормальные векторы
![]() и
и
![]() .
Отсюда, учитывая условие параллельности
векторов, получаем условие параллельности
двух плоскостей:
.
Отсюда, учитывая условие параллельности
векторов, получаем условие параллельности
двух плоскостей:
![]()
![]() .
.
Если
![]() ,
то
и, значит, условие перпендикулярности
двух плоскостей имеет вид:
,
то
и, значит, условие перпендикулярности
двух плоскостей имеет вид:
![]() .
.
Угол между двумя плоскостями
Если коэффициенты
![]() и
и
![]() плоскостей
плоскостей
;
не пропорциональны, то плоскости P1 и P2 пересекаются по некоторой прямой L. Проведем плоскость P, перпендикулярную к линии L. Эта плоскость пересекается с P1 и P2 по прямым и . Угол между прямыми и называется углом между плоскостями P1 и P2.
Поскольку
![]() и
и
![]() ,
то угол между векторами
,
то угол между векторами
![]() и
и
![]() (
)
равен углу
между плоскостями P1
и P2. Тогда
равенство
(
)
равен углу
между плоскостями P1
и P2. Тогда
равенство
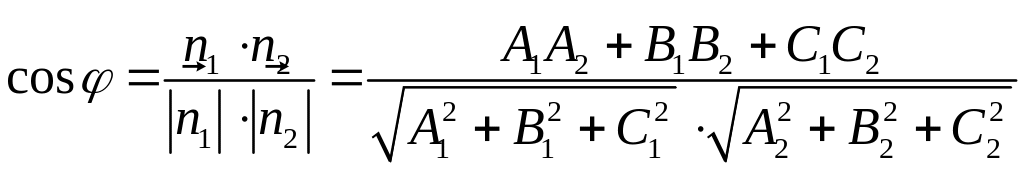 (5.7)
(5.7)
и определяет косинус искомого угла между плоскостями P1 и P2.
5.7. Расстояние от точки до плоскости
Пусть задана точка
и плоскость
![]() .
Расстояние от точки
до плоскости P находится
по формуле
.
Расстояние от точки
до плоскости P находится
по формуле
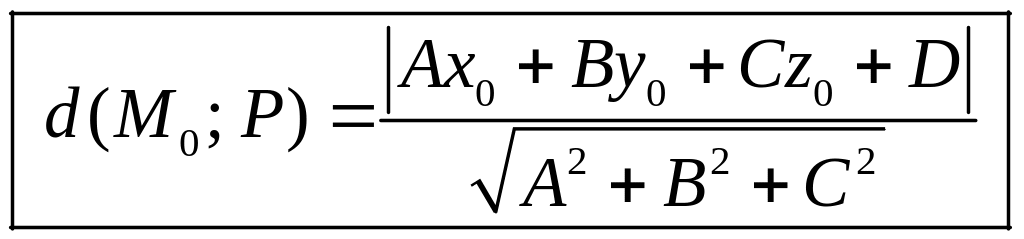 .
(5.8)
.
(5.8)
Вывод этой формулы такой же, как вывод формулы расстояния от точки до прямой.
Пример 5.3. Установить взаимное расположение заданных плоскостей. Если плоскости параллельные, то найти расстояние между плоскостями; если плоскости пересекаются, найти угол между плоскостями:
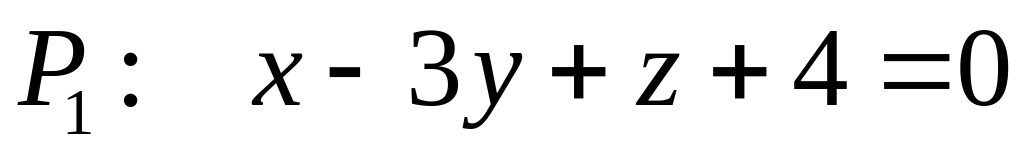 и
и
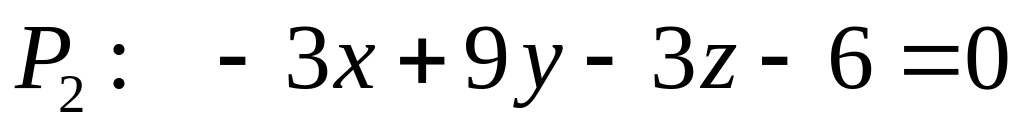 ;
; и
и
 .
.
Решение. 1) Определяем координаты
нормальных векторов данных плоскостей:
![]() и
и
![]() .
Так как выполняется условие
.
Так как выполняется условие
![]() ,
то плоскости P1
и P2 параллельны.
,
то плоскости P1
и P2 параллельны.
Например, в плоскости P2
выберем точку M,
принадлежащую этой плоскости. Для этого,
например, придадим переменным x
и y значения равные
нулю, т.е.
и
,
и найдем z:
![]()
![]() .
Значит
.
Значит
![]() .
Найдем расстояние от точки M
до плоскости P1:
.
Найдем расстояние от точки M
до плоскости P1:
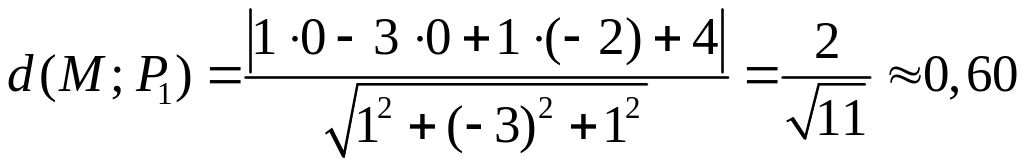 .
.
2) Определяем координаты нормальных
векторов данных плоскостей:
![]() и
и
![]() .
Так как выполняется условие
.
Так как выполняется условие
![]() ,
то плоскости P1
и P2 не являются
параллельны. Значит, они пересекаются.
,
то плоскости P1
и P2 не являются
параллельны. Значит, они пересекаются.
Используя формулу (5.8) находим косинус угла между этими плоскостями:
 .
.
Тогда
![]() .
.
6. Уравнение прямой
В ПРОСТРАНСТВЕ
6.1. Канонические и параметрические уравнения прямой
Прямая L в пространстве определяется однозначно, если:
а) известны точка, через которую она проходит, и ненулевой вектор, параллельный прямой;
б) или известны две точки этой прямой.
Постановка задачи: Составить
уравнение прямой, проходящей через
точку
,
и параллельной вектору
![]() .
Вектор
называется направляющим вектором
прямой.
.
Вектор
называется направляющим вектором
прямой.
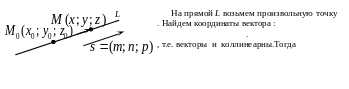
![]() .
(6.1)
.
(6.1)
Равенства (6.1) называются каноническими уравнениями прямой в пространстве.
Пусть
![]() и
радиус-векторы
точек
и
соответственно. Тогда три вектора
и
радиус-векторы
точек
и
соответственно. Тогда три вектора
![]() ,
,
![]() и
связаны соотношением
и
связаны соотношением
![]() .
(6.2)
.
(6.2)
Так как векторы
и
![]() коллинеарны, то существует число
,
такое, что
коллинеарны, то существует число
,
такое, что
![]() .
Тогда из уравнения (6.2) имеем
.
Тогда из уравнения (6.2) имеем
![]() .
(6.3)
.
(6.3)
Соотношение (6.3) называется векторным параметрическим уравнением прямой в пространстве. В координатной форме уравнение (6.3) равносильно трем уравнениям
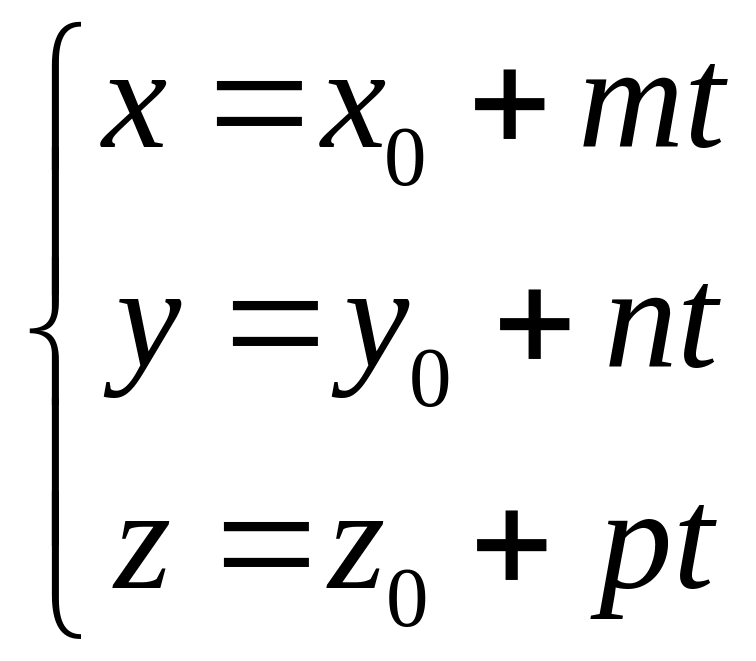 ,
,
(6.4)
,
,
(6.4)
Равенства (6.4) называются параметрическими уравнениями прямой в пространстве.
Замечание. Уравнение (6.1) можно было бы получить сразу из параметрических уравнений прямой (6.4), исключив параметр . Из уравнений (6.4) находим
![]() .
.
