1.5. Разные замечания. В этом пункте мы приведем некоторые замечания и дополнения к теореме 1.1.

Одно обобщение теоремы 1.1. Теорема 1.1 является частным случаем одной абстрактной теоремы, в которой речь идет об абстрактных пространствах и и абстрактном операторе ; см. Лионс и Мадженес [1].

Если взамен (1.28) мы предположим, что

(1.80)

то все утверждения теоремы 1.1 верны с одним только изменением:

(1.81)

В доказательстве существования мы пишем после (1.47)

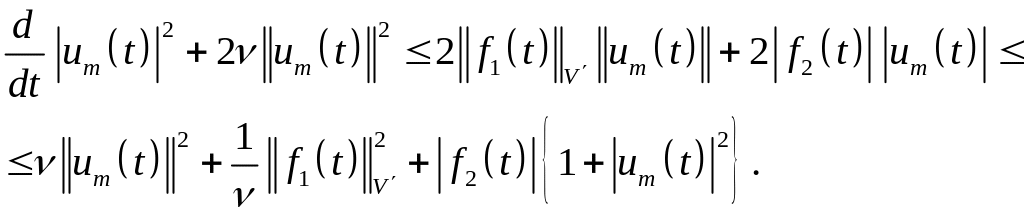
(1.82)

Отсюда

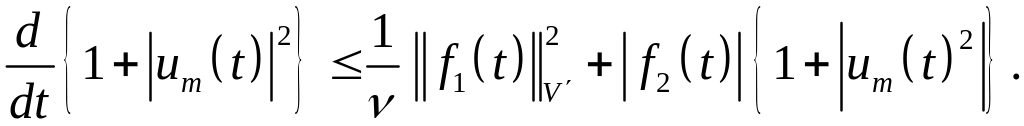(1.83)

Умножая это на , приходим к неравенству

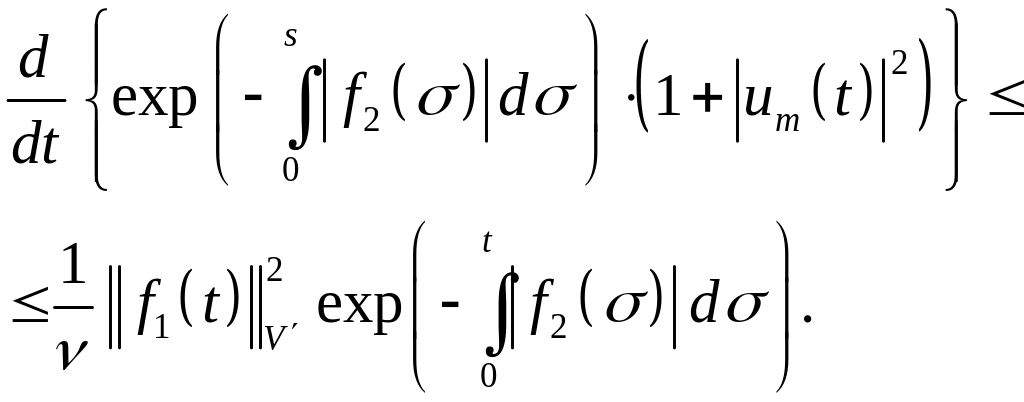
Интегрируя его от , получаем равномерную по оценку, аналогичную (1.50), откуда следует (1.51). Интегрируя затем (1.82) от до , получаем (1.53). Доказательство существования проводится далее в точности так же, как в п. 1.3. Что касается производной , то мы имеем

(1.84)

Легко видеть, что лемма 1.2 верна также, если

(1.85)

Заметив это, мы можем доказать единственность и непрерывность точно так же, как в п. 1.4.

Случай неограниченной области .

Для эволюционной задачи при рассмотрении неограниченных областей введение пространства , привлекавшегося в стационарном неограниченном случае (гл. I, п. 2.3), не является более необходимым. Все предыдущие результаты остаются верными, если область неограниченна, а снабжено нормой 1.9. Предположим, в самом общем случае, что удовлетворяет (1.80). Мы имеем в точности такие же результаты, как в теореме 1.1, если удовлетворяет (1.28), и такие же результаты, как в теореме 1.1, если удовлетворяет (1.80). Единственное отличие заключается в том, что мы должны вместо (1.80) использовать следующее неравенство:

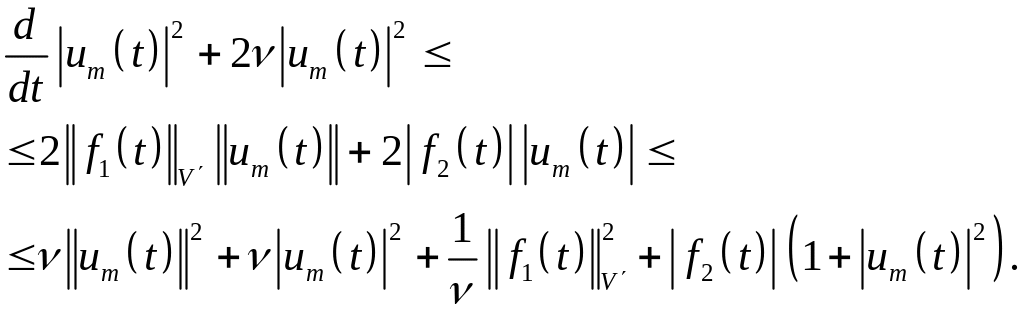(1.86)

Отсюда

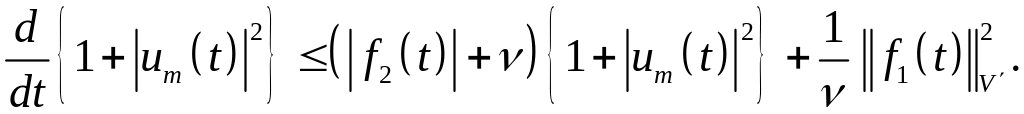(1.87)

К этому неравенству применяется далее точно та же процедура, что и к неравенству (1.83), для получения утверждения (1.51). После этого, интегрируя (1.86) от до , приходим к оценке

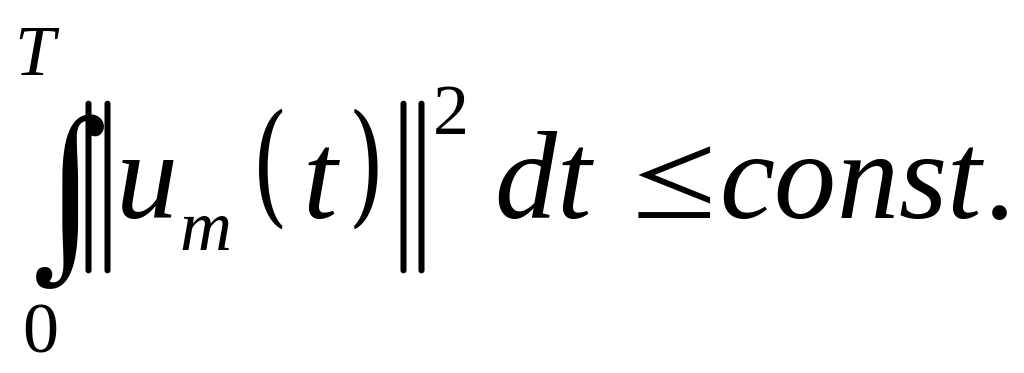
Эта оценка вместе с (1.51) дает (1.53). Доказательство существования единственности и непрерывности решения проводится далее точно так же, как выше.

Интерпретация вариационной задачи.

Мы хотим теперь уточнить, в каком смысле функция , определяемая теоремой 1.1, является решением исходной задачи (1.23) – (1.26).