Доказательство непрерывности и единственности.
Это доказательство основывается на следующей лемме, которая является частным случаем интерполяционной теоремы Лионса – Мадженеса [1]:
Лемма 1.2. Пусть
тройка
гильбертовых пространств, каждое из
которых вложено в последующее как в
(1.5), причем
пространство,
сопряженное к
.
Если функция
принадлежит
,
а ее производная
принадлежит
,
то
п.в. равна некоторой непрерывной функции
из
в
и имеет место следующее равенство,
которое выполняется в смысле скалярных
распределений на
:
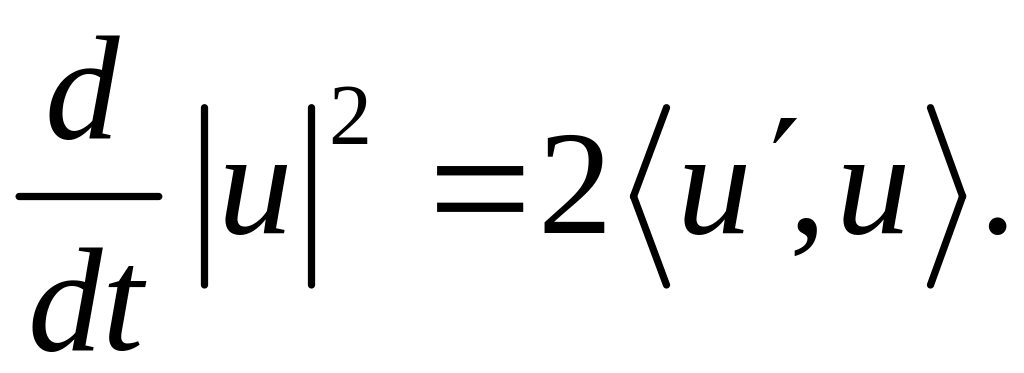(1.68)
Равенство (1.68)
имеет смысл, так как обе функции
интегрируемы на
Ниже мы дадим доказательство этой леммы, более элементарное, чем приведенное у Лионса и Мадженеса [1].
Если принять, что
лемма уже доказана, то (1.39) становится
очевидным, и остается только проверить
единственность решения. Предположим,
что
и
два
решения задачи (1.36) – (1.38), и пусть
.
Тогда
принадлежит тем же пространствам, что
и
,
и
(1.69)
Умножая первое
равенство (1.69) скалярно на
,
находим, что
п.в.
Используя теперь (1.68) с , замененным на , получаем
откуда
для каждого
.
Тем самым доказательство теоремы 1.1.
полностью завершено.
Доказательство леммы 1.2.
Элементарное доказательство леммы 1.2, о котором упоминалось выше, мы оформим в виде двух следующих лемм.
Лемма 1.3. В предположениях леммы 1.2 справедливо равенство (1.68).
Доказательство.
Регуляризуя функцию
,
действующую из
в
и равную
на
и
вне этого интервала, мы легко получаем
последовательность функций
,
удовлетворяющую условиям
для всякого есть бесконечно дифференцируемая функция
из в ; (1.70)
при
в
в
(1.71)
Ввиду (1.6) и (1.70) равенство (1.68) очевидным образом выполняется для :
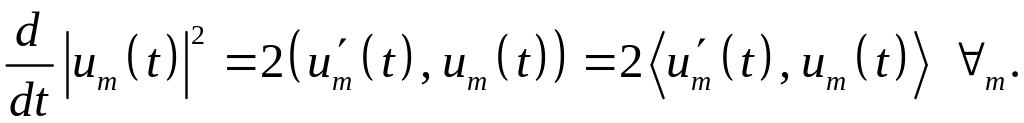(1.72)
Из (1.71) следует, что при
в
в
Здесь сходимость также понимается в смысле теории распределений; итак, мы можем перейти к пределу в (1.72) в смысле теории распределений; в пределе получим в точности (1.68).
Так как функция
интегрируема на
,
равенство (1.68) показывает, что функция
из леммы 1.3 удовлетворяет условию
(1.73)
В том частном случае, когда функция удовлетворяет (1.36) – 1.38), это было доказано непосредственно, в п.1.3.
Согласно лемме
1.1,
непрерывная
функция из
в
Поэтому, используя еще (1.73) и приводимую
ныне лемму 1.4, получаем, что
сладо
непрерывная функция из
в
,
т.е.
функция
непрерывна. (1.74)
Приняв пока на
веру этот факт, мы можем завершить
доказательство леммы 1.2. Нам надо
показать, что для каждого
при
(1.75)
Распишем выражение слева:
Когда
.
Действительно, в силу (1.68),
а в силу (1.74),
.
Тем самым (1.75) доказано.
Используемую в доказательстве леммы 1.2 лемму мы сформулируем в немного более общем виде, чем это нам нужно.
Лемма 1.4. Пусть
и
два
банаховых пространства, таких, что
(1.76)
причем вложение
непрерывно. Если функция
принадлежит
и слабо непрерывна как функция со
значениями в
,
то
слабо непрерывна как функция со значениями
в
Доказательство.
Заменив, если надо,
на замыкание
в
,
мы можем считать, что
плотно в
.
Тогда плотное непрерывное вложение
в
дает по двойственности плотное непрерывное
вложение
(сопряженного к
)
в
(сопряженное к
):
(1.77)
По предположению,
для каждого
при
(1.78)
и нам надо показать, что (1.78) верно также для каждого .
Покажем сначала,
что
для каждого
и
(1.79)
В самом деле,
регулярную функцию
,
равную
на
и
вне этого интеграла, мы получаем
последовательность функций
,
действующих из
в
,
таких, что
и
при
Так как
мы получаем в пределе
Из этого равенства следует включение и неравенство (1.79).
Наконец, докажем
(1.78) для
.
Так как
плотно в
,
то
такое, что
.
Запишем
Так как
,
то по предположению о непрерывности
имеем
при
и, следовательно,
Так как произвольно мало, то этот верхний предел равен , и (1.78) доказано.