2.5. Метод параболической аппроксимации

В этом методе функция f(x) заменяется не линейной, а параболической функцией, что является более точной заменой. Следовательно, метод может обеспечить более быструю сходимость к решению. На первом этапе параболу обычно строят по трем точкам: крайним и средней точкам интервала (а, b), где отделен корень, т.е. (а, f(а)), ((а+b)/2, f((а +b)/2)), (b, f(b)). По полученному уравнению параболы у = с₂ x²+с₁х+c₀ находят приближенный корень (приближенный потому что парабола приближённо заменяет f(x)), для чего решают уравнение с₂х²+с₁х+c₀=0. На втором этапе строят параболу по трём точкам: найденному приближенному корню и двум предыдущим точкам (слева и справа от этой точки), лежащим по разные стороны оси х. Такой вариант выбора точек на практике быстрее приводит к решению по сравнению с вариантом, когда для построения параболы берутся последовательно три последние точки. Эта процедура повторяется многократно до тех пор, пока величина отрезка, внутри которого находится корень, не будет меньше e – предварительно заданной погрешности.

На рис. 4.4 приведён один шаг уточнения корня методом параболической аппроксимации. Начальная парабола проведена через точки a, c, b (здесь c, является серединой отрезка [а, b]); х – пересечение параболы с осью x. Следующая парабола должна проводиться через точки (c, f(c)), (х, f(x)), (b, f(b)).

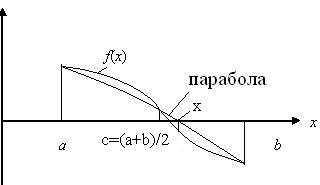
Рис. 4.4. Параболическая аппроксимация

2.6. Метод простой итерации

Рассматриваемый метод реализует третий подход из представленных в концепции. Предварительно исходное уравнение f(x) = 0 преобразуют к виду (x) = х, что является частным случаем более общей структуры g(x) = f(x). Затем выбирают начальное значение x₀ и подставляют его в левую часть уравнения, но (x₀)  x₀, поскольку x₀ взято произвольно и не является корнем уравнения. Полученное (x₀) = x₁ рассматривают как очередное приближение к корню. Его снова подставляют в левую часть уравнения (x₁) и получают следующее значение х₂ (х₂ = (x₁)) и т.д. В общем случае x_i+1=(x_i). Получающаяся таким образом последовательность x₀, х₁, х₂, х₃, ... при определённых условиях может сходиться к корню х*. Таким условием является |'(х)|1 на [а,b], причём, чем ближе модуль к нулю, тем выше окажется скорость сходимости к решению. В противном случае последовательность расходится от искомого решения ("метод не сходится").

Существуют различные способы преобразования уравнения (х)=0 к виду (х)=х; одни могут привести к выполнению условия сходимости всегда, другие – только в отдельных случаях. Самый простой способ следующий:

(x)+х=0+x, (x)+х= (х) ==> (х)=х,

но он не всегда приводит к успеху. Существует другой способ, в соответствии с которым (х)=х–(х)/k, причем k следует выбирать так, чтобы |k > Q/2, где и знак k совпадал бы со знаком f’(x) на [a, b].

3. Реализация метода половинного деления для уточнения корня

Исходное уравнение преобразуется к виду f(x)=0. Для отделения искомого корня строится таблица значений и график функции f(x) на отрезке [a,b], заданном из области определения функции. Для этого используется программа, разработанная в предыдущих лабораторных работах. Например, для уравнения f(x)=0 с функцией f(x)=6/x–3xe^x+x²–4 задаётся интервал [-5,-0.5] из области определения (-,0)U(0,+). На рис. 4.5 показаны таблица значений и график рассматриваемой функции. Как видно из таблицы и графика на интервале [-3,-2] функция f(x) меняет знак с + на –. Следовательно, на этом интервале она пересекает ось абсцисс (принимает значение 0). Поэтому данный интервал надо задать в качестве исходного для уточнения корня по одному из методов: половинного деления, хорд, комбинированный, параболической аппроксимации. Для методов Ньютона и простой итерации в качестве начального приближения следует задать одну из границ выбранного интервала.

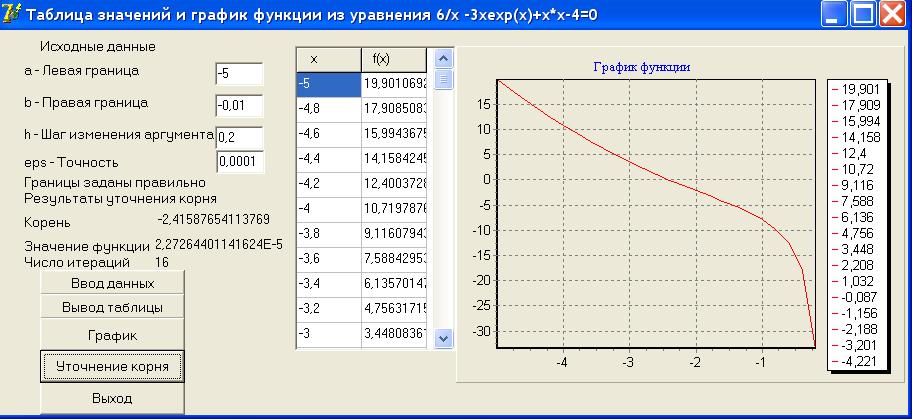
Рис. 4.5. Результаты отделения и уточнения корня уравнения

На рис. 4.5 показан общий вид окна программы для отделения и уточнения корня нелинейного уравнения 6/x–3xe^x+x²–4=0. Объект Edit4 используется для ввода заданной точности eps. Объекты Label5, Label9, Label11Label13 используются для отображения соответствующих пояснений к результатам уточнения корня. Объекты Label16Label8 – для вывода результатов вычислений: корня уравнения, значения функции и количества итераций по уточнению корня. Объект Label10 используется для вывода соответствующего сообщения о правильности задания интервала [a, b] (например, при a > b будет выдано сообщение «Границы заданы неправильно»). Кнопка Button5, с определённым для неё названием (поле Caption) «Уточнение корня», используется для вызова подпрограммы уточнения корня по методу половинного деления.