Лабораторная работа 4 Решение алгебраических и трансцендентных уравнений
Цель занятия – ознакомление с методами и приобретение навыков решения нелинейных алгебраических и трансцендентных уравнений.
1. Общие сведения и постановка задачи
Многие инженерные задачи, такие как определение установившихся режимов или нахождения положений равновесия электромеханических систем, сводятся к решению трансцендентных уравнений, т.е. отысканию таких значений аргумента x, при которых уравнение f(x)=0 обращается в тождество. Здесь f –заданная непрерывная функция аргумента x.
Класс трансцендентных уравнений является настолько широким, что общего метода их решения пока не существует. Имеющиеся методы решения трансцендентных уравнений включают два этапа:
отделения корня, т.е. определение интервала значений аргумента, на котором содержится искомый корень;
уточнение корня, т.е. сокращение интервала, содержащего искомый корень, до величины, соответствующей требуемой точности определения корня.
На этапе отделения корня интервал должен быть определён так, чтобы в нем было гарантировано существование корня. Для этого используют дополнительные сведения о характере решаемого уравнения, предварительное значение интервала может быть выбрано из общефизических соображений. Если такие подходы не могут быть использованы, тогда приходится с достаточно большим шагом исследовать всю область допустимых значений (ОДЗ) функции f(x), чтобы обнаружить интервал, на котором существует корень уравнения f(x)=0. Для этого следует использовать программу построения графика или табулирования функции f(x) (построения таблицы значений функции) при изменении аргумента x с заданным шагом h на интервале, выбранном из области определения функции. Если f(x) – непрерывная функция, то на границах интервала, где существует корень, функция будет иметь разный знак. Необходимо иметь в виду, что при выполнении этого условия на интервале может существовать нечетное количество корней, тогда как при существовании на интервале четного количества корней функция на границах интервала будет иметь одинаковый знак, и предлагаемый критерий такие корни не зафиксирует. Это показывает, насколько сложна и неопределенна задача отделения корней произвольного трансцендентного уравнения.
2. Численные методы решения нелинейных алгебраических и трансцендентных уравнений
В отличие от задачи отделения корней, задача уточнения корня может быть успешно алгоритмизирована. Наиболее широко для уточнения корня используются метод половинного деления, метод хорд и метод Ньютона (метод касательных).
2.1. Метод половинного деления
Алгоритм уточнения корня методом половинного деления заключается в последовательном делении пополам интервала, на котором присутствует корень.
Рассмотрим функцию f(x), которая на границах интервала [a, b] принимает значения f(a) и f(b), имеющие разные знаки (рис.4.1). В предположении о непрерывности f(x) это гарантирует существование корня на рассматриваемом интервале.
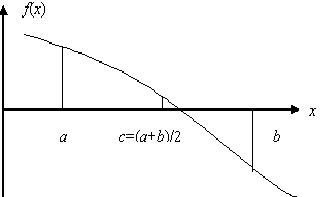
Рис. 4.1. Деление отрезка пополам
Найдем значение функции f(c) в середине рассматриваемого интервала с=(a+b)/2. В зависимости от соотношения знаков f(a) и f(с) для следующего шага алгоритма выбирается подинтервал [a, c] или [c, b]. Если знаки функции на концах интервала [a,c] совпадают, то в качестве левой границы нового интервала принимается точка с. Если знаки f(a) и f(c) различны, то точка с принимается за правую границу интервала. В этом новом интервале отыскивается его средняя точка, отбрасывается одна половина интервала, и этот процесс продолжается до тех пор, пока оставшийся интервал не станет меньше допустимой погрешности определения корня e.
Достоинством метода половинного деления является гарантия получения решения при весьма слабых ограничениях на вид функции f(x).
Основной недостаток – медленная сходимость, что требует большого количества повторения вычислений (итераций). Поскольку при каждом повторении интервал сокращается в два раза, то при n‑кратном повторении интервал сократится в 2n раз. Для сокращения интервала в 1024 раз требуется 10 повторений, для сокращения в 1048576 раз требуется 20 повторений.