2.2. Метод хорд
Более быструю сходимость может обеспечить метод хорд. Но он оказывается тем более эффективным, чем более гладкой является функция f(x) на рассматриваемом интервале.
В отличие от метода половинного деления точка c выбирается на пересечении хорды, соединяющей значения функции на границах интервала, с осью абсцисс (рис.4.2).
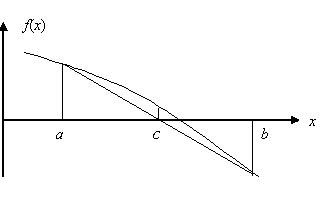
Рис.4.2. Метод хорд
Формула для вычисления точки c=[b f(a)–a f(b)]/[f(a)–f(b)]. Для точки с вычисляется значение функции f(c).
Из двух подинтервалов (a, c) и (c, b) выбирается тот, на котором существует корень, и вычисления повторяются до тех пор, пока оставшийся интервал не станет меньше допустимой погрешности уточнения корня.
Метод хорд применим только для монотонных функций.
Сходимость метода зависит от свойств функции f(x). Если f(b) f’’(b)>0 то строящаяся на каждой итерации хорда будет иметь правый фиксированный («закрепленный») конец. Итерационная формула для уточнения корня будет иметь вид
.
При этом последовательность x1, x2, … будет приближаться к корню слева. Если же f(a) f’’(a)>0, то строящаяся на каждой итерации хорда будет иметь левый фиксированный («закрепленный») конец и итерационная формула для уточнения корня будет иметь вид
.
При этом последовательность x1,x2,… будет приближаться к корню справа.
2.3. Метод Ньютона
Чтобы более эффективно использовать гладкость функции f(x), можно воспользоваться методом Ньютона, который называется также методом касательных. Метод Ньютона требует, чтобы кроме функции f(x) была известна и её первая производная f’(x)=df(x)/dx. Предположим, что приближенное значение корня равно x1 (рис.4.3).
Рис. 4.3. Метод Ньютона (касательных)
Функция f(x) в этой точке равна f(x1). Заменяя f(x) касательной в т. x1, найдём следующее приближение корня x2=x1–(f(x1)/f’(x1)). В точке x2 вновь вычисляется f(x2) и производная f’(x2)=d f(x)/dx/x=x2 и определяется очередное приближение x3. Так продолжается до тех пор, пока модуль разности двух последовательных приближений корня не станет меньше допустимой погрешности отыскания корня.
В общем виде итерационная формула метода Ньютона выглядит следующим образом
xi+1=xi – f(xi)/f’(xi).
Метод Ньютона обеспечивает достаточно быструю сходимость, если f(x) – выпуклая монотонная функция, но может оказаться расходящимся в других случаях. Следует обратить внимание на следующую особенность метода Ньютона: последовательность х1, х2, x3, ... приближается к корню с другой стороны, чем при использовании метода хорд при прочих равных условиях.
2.4. Комбинированный метод
Данный метод, так же как и предыдущие, базируется на замене нелинейной функции f(x) линейной. Но с учётом стремления к корню метода хорд и метода Ньютона с разных сторон для повышения эффективности используются оба алгоритма одновременно. Один шаг делается методом хорд, а следующий (с другой стороны) – методом Ньютона. При этом интервал, где содержится корень, сокращается с обеих сторон, что обусловливает другое условие окончания поиска. Поиск можно прекратить, как только разница между правым и левым концами интервала станет меньше предварительно заданной погрешности e.
Алгоритмы используемых методов следует выбирать с учетом упомянутых выше особенностей функций.