
ЛЕКЦИЯ № 2.4
по дисциплине «Системный анализ и принятие решений»
Тема № 2. Математические методы моделирования систем
Симплекс-метод Вопросы занятия
1 Вычислительный алгоритм симплекс-метода
2 Особенности решения задачи с двухсторонними ограничениями и ненулевыми граничными условиями
Литература
1 Справочник по оптимизационным задачам в асу/ в. А. Бункин, д. Колев, б. Я. Курицкий и др. – л.: Машиностроение, 1984. – 212 с.
2 Терехов Л. Л. Экономико-математические методы: учебник. – М.: Наука, 1972. – 360 с.
3 Зуховицкий С. И. Математические методы сетевого планирования / С. И. Зуховицкий, И. А. Радчик. – М.: Наука, 1965. – 296 с.
4 Экономико-математические методы и модели. Компьютерные технологии решения: учеб. пособие/ И. Л. Акулич, Е .И. Велесько, П. Ройш, В. Ф. Стрельчонок. – Мн.: БГЭУ, 2003. – 348 с.
+5 Бережная Е. В., Бережной В. И. Математические методы моделирования экономических систем: учеб. пособие. – М.: Финансы и статистика, 2003. – 368 с.
Введение
Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём направленного перебора вершин выпуклого многогранника (симплекса) в многомерном пространстве (например, вершин треугольника на плоскости, вершин четырёхгранника в 3–мерном пространстве) до определения координат вершины, в которой целевая функция принимает оптимальное значение.
Первый метод линейного программирования, названный методом разрешающих множителей, разработан Л. В. Канторовичем в 1939 году [Л. В. Канторович. Математические методы организации и планирования производства. Л.: Изд-во ЛГУ, 1939]. Симплекс-метод был разработан американским математиком Джорджем Данцигом (George Dantzig) в 1947 году.
Разновидностями симплекс-метода (модифицированный, с обратной матрицей, двойственный и другие) используется один и тот же математический подход к решению задачи линейного программирования, который рассматривается на примере вычислительного алгоритма. Во втором вопросе представлены общая постановка задачи линейного программирования и методы её решения.
1 Вычислительный алгоритм симплекс-метода
Вычислительный алгоритм симплекс-метода применяется для решения задачи линейного программирования (ЛП) с односторонним ограничением и требованием неотрицательности переменных:
 (1)
(1)
Алгоритм симплекс-метода включает пять этапов, которые рассмотрим на примере решения следующей задачи ЛП:
 (2)
(2)
Этап 1. Представить исходные данные в виде симплекс-таблицы.
Вводим дополнительные
(базисные) переменные y
в ограничения и записываем задачу в
стандартной форме (предварительно
записываем систему таким образом, чтобы
в ограничениях были знаки «![]() »,
и вводим дополнительные переменные):
»,
и вводим дополнительные переменные):
 (3)
(3)
Значения свободного члена c0 и коэффициентов cj, при свободных переменных x в уравнении целевой функции, свободных членов bi и коэффициентов аij при свободных переменных в уравнениях ограничений записываем в симплекс-таблицу (таблица 1).
Таблица 1
|
Свободный член |
x1 |
x2 |
x3 |
E |
0 |
-2 |
2 |
1 |
y1 |
1 |
-1 |
-1 |
1 |
y2 |
-5 |
-2 |
0 |
-1 |
y3 |
2 |
1 |
1 |
0 |
y4 |
2 |
0 |
2 |
1 |
Этап 2. Проверить совместимость ограничений (наличие ОДР).
Признак 1. Ограничения совместимы, если на каждой итерации (результате повторения математической операции) в каждой строке, имеющей отрицательный свободный член, есть хотя бы один отрицательный элемент.
Из таблицы 1 видно, что признак 1 выполняется.
Этап 3. Найти допустимое решение (координаты любой вершины ОДР).
Признак 2. Решение является допустимым, если в строках базисных переменных симплекс-таблицы все свободные члены неотрицательные.
Из таблицы 1 видно, что признак 2 не выполняется.
Если это требование не выполняется, производится обмен переменных. На каждой итерации такого обмена одна переменная из свободных переводится в базисные, а одна базисная – в свободные.
Алгоритм перехода при обмене переменных состоит из пяти шагов.
1 Числа, содержащиеся в исходной симплекс-таблице, записать в верхних левых частях ячеек новой симплекс-таблицы.
2 Выбрать разрешающий элемент.
В строке, содержащей отрицательный свободный член, выбрать отрицательный элемент. Столбец, в котором находится выбранный элемент, принять в качестве разрешающего.
От выбора разрешающего столбца зависит число итераций, в результате которых находится допустимое решение. Для выбора разрешающего столбца проводится сложный анализ. На оптимальное решение выбор столбца не влияет.
В качестве разрешающего столбца могут быть приняты столбцы x1 и x3. Разрешающим принят столбец x1.
В разрешающем столбце
для всех элементов аij,
имеющих одинаковый знак со свободным
членом bi,
определить отношение bi/аij.
Значение
![]() может быть равно нулю. Строку с минимальным
значением bi/аij
выбрать в качестве разрешающей.
может быть равно нулю. Строку с минимальным
значением bi/аij
выбрать в качестве разрешающей.
Для
рассматриваемого примера
![]() и в качестве разрешающей принимаем
строку y3.
и в качестве разрешающей принимаем
строку y3.
Разрешающим элементом принимается элемент, принадлежащий разрешающим столбцу и строке.
3 Заполнить нижние правые части ячеек симплекс-таблицы по следующим правилам:
1) ячейку
разрешающего элемента заполнить
![]() ,
где
,
где
![]() –разрешающий
элемент;
–разрешающий
элемент;
2) ячейки
разрешающей строки заполнить элементами,
стоящими в этих ячейках, умноженными
на
![]() ;
;
3) ячейки разрешающего столбца заполнить элементами, стоящими в этих ячейках, умноженными на минус ;
4) выделить в разрешающей строке все верхние числа, а в разрешающем столбце – все нижние числа;
5) все остальные ячейки заполнить произведением выделенных чисел, находящихся в той же строке и в том же столбце, в которых расположена данная ячейка.
Таблица 1 преобразована в таблицу 2.
Т аблица
2
аблица
2
x1 |
y3 |
||||
|
Свободныйчлен |
x1 |
x2 |
x3 |
|
E |
0 4 |
-2 2 |
2 2 |
1 0 |
|
y1 |
1 2 |
-1 1 |
-1 1 |
1 0 |
|
y2 |
-5 4 |
-2 2 |
0 2 |
-1 0 |
|
y3 |
2 2 |
1 1 |
1 1 |
0 0 |
|
y4 |
2 0 |
0 0 |
2 0 |
1 0 |
|
4 Перейти к следующей симплекс-таблице.
В новой симплекс-таблице:
1) поменять местами обмениваемые переменные;
2) в разрешающих строке и столбце записать в верхней левой части каждой ячейки число, стоящее в нижней правой части данной ячейки;
3) в остальных ячейках записать в верхней левой части сумму двух чисел, стоящих в каждой ячейке.
Новая симплекс-таблица представлена в таблице 3 (левые верхние части ячеек).
Т аблица
3
аблица
3
x3 |
y2 |
||||
|
Свободныйчлен |
y3 |
x2 |
x3 |
|
E |
4 -1 |
2 2 |
4 2 |
1 1 |
|
y1 |
3 -1 |
1 2 |
0 2 |
1 1 |
|
y2 |
-1 1 |
2 -2 |
2 -2 |
-1 -1 |
|
x1 |
2 0 |
1 0 |
1 0 |
0 0 |
|
y4 |
2 -1 |
0 2 |
2 2 |
1 1 |
|
5 Проверить признаки.
Если признак 2 выполняется, полученное решение является допустимым. В противном случае проверяется признак 1. Если признак 1 выполняется, то обмен переменных повторяется ещё раз. В противном случае допустимое решение получено быть не может.
Из таблицы 3 видно, что признак 2 не выполняется, а признак 1 выполняется.
Повторяем обмен переменных.
Результаты повторного обмена переменных представлены в таблице 4. Признак 2 выполняется и значения в таблице 4 являются допустимым решением рассматриваемого примера.
Таблица 4
|
Свободный член |
y3 |
x2 |
y2 |
E |
3 |
4 |
6 |
1 |
y1 |
2 |
3 |
2 |
1 |
x3 |
1 |
-2 |
-2 |
-1 |
x1 |
2 |
1 |
1 |
0 |
y4 |
1 |
2 |
4 |
1 |
Из таблицы 4 следует, что x1=2; x3=1; y1=2; y4=1; y3=x2=y2=0; E=3 (см. столбец свободного члена).
Этап 4. Проверить наличие оптимального решения, то есть ограниченность целевой функции.
Признак 3а. Целевая функция имеет минимальное значение (ограничена снизу), если на каждой итерации в каждом столбце, в строке целевой функции которого находится положительный элемент, есть хотя бы один положительный элемент.
Признак выполняется для таблиц 2; 3; 4.
Признак 3б. Целевая функция имеет максимальное значение (ограничена сверху), если на каждой итерации в каждом столбце, в строке целевой функции которого находится отрицательный элемент, есть хотя бы один положительный элемент.
Этап 5. Найти оптимальное решение.
Признак 4а. Целевая функция имеет максимальное значение в том случае, когда в строке целевой функции все элементы, кроме свободного члена, который не рассматривается, положительные.
Признак 4б. Целевая функция имеет минимальное значение в том случае, когда в строке целевой функции все элементы, кроме свободного члена, который не рассматривается, отрицательные.
Признак 4в. Если в строке целевой функция все элементы, кроме свободного члена, который не рассматривается, одного знака и при этом есть хотя бы один нулевой элемент, то полученное нулевое решение является альтернативным.
Последнее означает, что есть и другой набор значений переменных, при которых целевая функция имеет такое же оптимальное значение.
Признак 4б для симплекс-таблицы 4 не выполняется. В этом случае продолжается обмен переменных так же, как при поиске допустимого решения, за исключением: разрешающим принимается столбец, в строке целевой функции которого находится элемент, не соответствующий по знаку проверяемому признаку.
Очередные симплекс-таблицы для рассматриваемого примера представлены в таблицах 5-7.
В таблице 7 признак 4б выполняется и полученное решение является оптимальным (в смысле минимума целевой функции). При x1=3/2; x3=2; y1=1/2; y3=1/2; x2=y4=y2=0; min E=1.
Т аблица
5
аблица
5
x2 |
y4 |
||||
|
Свободныйчлен |
y3 |
x2 |
y2 |
|
E |
3 -3/2 |
4 -3 |
6 -3/2 |
1 -3/2 |
|
y1 |
2 -1/2 |
3 -1 |
2 -1/2 |
1 -1/2 |
|
x3 |
1 1/2 |
-2 1 |
-2 1/2 |
-1 1/2 |
|
x1 |
2 -1/4 |
1 -1/2 |
1 -1/4 |
0 -1/4 |
|
y4 |
1 1/4 |
2 1/2 |
4 1/4 |
1 1/4 |
|
Т аблица 6
y3 |
x2 |
||||
|
Свободныйчлен |
y3 |
y4 |
y2 |
|
E |
3/2 -1/2 |
1 -2 |
-3/2 -1/2 |
-1/2 -1/2 |
|
y1 |
3/2 -1 |
2 -4 |
-1/2 -1 |
1/2 -1 |
|
x3 |
3/2 1/2 |
-1 2 |
1/2 1/2 |
-1/2 1/2 |
|
x1 |
7/4 -1/4 |
1/2 -1 |
-1/4 -1/4 |
-1/4 -1/4 |
|
x2 |
1/4 1/2 |
1/2 2 |
1/4 1/2 |
1/4 1/2 |
|
Таблица 7
|
Свободный член |
x2 |
y4 |
y2 |
E |
1 |
-2 |
-2 |
-1 |
y1 |
1/2 |
-4 |
-3/2 |
-1/2 |
x3 |
2 |
2 |
1 |
0 |
x1 |
3/2 |
-1 |
-1/2 |
-1/2 |
y3 |
1/2 |
2 |
1/2 |
1/2 |
2 Особенности решение задачи с двухсторонними ограничениями и ненулевыми граничными условиями
Задача ЛП с двухсторонними ограничениями и ненулевыми граничными условиями записывается в виде:
 (4)
(4)
Каждое ограничение и граничное условие можно представить в виде двух неравенств:
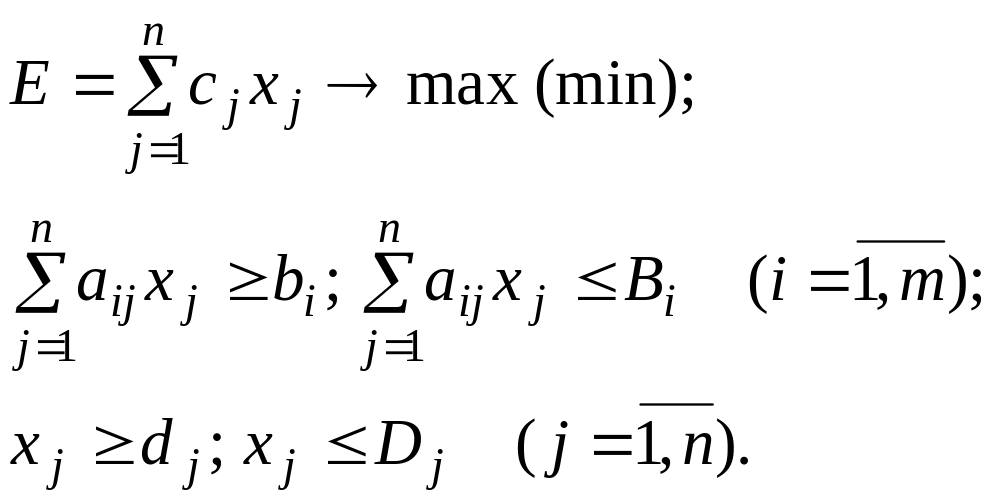 (5)
(5)
Таким образом, задача приводится к виду задачи (1).
Задача (1) решается с числом ограничений m и числом основных и дополнительных переменных m+n. Следовательно, размерность задачи с учётом целевой функции и столбца свободных членов составляет (m+1)(m+n+1).
Задача (5) решается с числом ограничений 2m+2n и числом основных и дополнительных переменных n+2m+2n=2m+3n. Следовательно, размерность задачи составляет (2m+2n+1)(2m+3n+1). Для решения задачи такой большой размерности применяется модифицированный симплекс-метод с мультипликативным представлением обратной матрицы [3].
При
использовании данного метода вместо
матрицы размерностью (2m+2n+1)(2m+3n+1)
выделяется матрица размерностью
(q+1)(q+2),
где
![]() .Таким
приёмом обеспечивается решение задач
большей размерности с помощью
последовательного решения задач меньшей
размерности.
.Таким
приёмом обеспечивается решение задач
большей размерности с помощью
последовательного решения задач меньшей
размерности.
Профессор В. П. Фандеев

