Теорема о циркуляции

Поскольку электростатическое поле является центральным, то силы, действующие на заряд в таком поле, являются консервативными (см. любой учебник по механике). Так как Edl представляет собой элементарную работу, которые силы поля производят над единичным зарядом, а работа консервативных сил на замкнутом пути равна нулю, то

(2.18)

Это утверждение называется теоремой о циркуляции вектора E.

Теорема Стокса — одна из основных теорем дифференциальной геометрии и математического анализа об интегрированиидифференциальных форм, которая обобщает несколько теорем анализа. Названа в честь Дж. Г. Стокса.

Общая формулировка

Пусть на ориентируемом многообразии   размерности   заданы ориентируемое  -мерное подмногообразие   идифференциальная форма   степени   класса   ( ). Тогда, если граница подмногообразия   положительно ориентирована, то

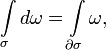
где   обозначает внешний дифференциал формы  .

Теорема распространяется на линейные комбинации подмногообразий одной размерности, так называемые цепи. В этом случае формула Стокса реализует двойственность между когомологией де Рама и гомологией циклов многообразия  .

Ро́тор, или вихрь — векторный дифференциальный оператор над векторным полем.

Обозначается

(в русскоязычной литературе) или

(в англоязычной литературе),

а также - как векторное умножение дифференциального оператора набла на векторное поле:

Результат действия этого оператора на конкретное векторное поле F называется ротором поля F или, короче, просто ротором F и представляет собой новое векторное^[1] поле:

Поле rot F (длина и направление вектора rot F в каждой точке пространства) характеризует в некотором смысле^[2] вращательную составляющую поля F соответственно в каждой точке.

Математическое определение

Ротор   векторного поля   — есть вектор, проекция которого   на каждое направление n есть предел отношенияциркуляции векторного поля по контуру L, являющемуся краем плоской площадки ΔS, перпендикулярной этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку:

.

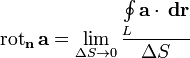Направление обхода контура выбирается так, чтобы, если смотреть в направлении  , контур L обходился по часовой стрелке^[3].

В трёхмерной декартовой системе координат ротор (в соответствии с определением выше) вычисляется следующим образом (здесьF - обозначено некое векторное поле с декартовыми компонентами  ; i, j, k - орты декартовых координат):

или

(что можно считать альтернативным определением, по сути совпадающим с определением в начале параграфа, по крайней мере при условии дифференцируемости компонент поля).

Для удобства можно формально представлять ротор как векторное произведение оператора набла (слева) и векторного поля:

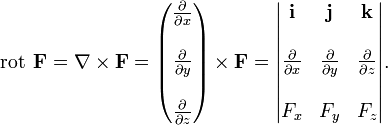
Закон кулона

Иначе: Два точечных заряда в вакууме действуют друг на друга с силами, которые пропорциональны произведению модулей этих зарядов, обратно пропорциональны квадрату расстояния между ними и направлены вдоль прямой, соединяющей эти заряды. Эти силы называются электростатическими (кулоновскими).

Важно отметить, что для того, чтобы закон был верен, необходимы:

1. точечность зарядов — то есть расстояние между заряженными телами много больше их размеров — впрочем, можно доказать, что сила взаимодействия двух объёмно распределённых зарядов со сферически симметричными непересекающимися пространственными распределениями равна силе взаимодействия двух эквивалентных точечных зарядов, размещённых в центрах сферической симметрии;

2. их неподвижность. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд;

3. взаимодействие в вакууме.

Однако с некоторыми корректировками закон справедлив также для взаимодействий зарядов в среде и для движущихся зарядов.^[1]

В векторном виде в формулировке Ш. Кулона закон записывается следующим образом:

где   — сила, с которой заряд 1 действует на заряд 2;   — величина зарядов;   — радиус-вектор (вектор, направленный от заряда 1 к заряду 2, и равный, по модулю, расстоянию между зарядами —  );   — коэффициент пропорциональности. Таким образом, закон указывает, что одноимённые заряды отталкиваются (а разноимённые — притягиваются).

Закон сохранения электрического заряда гласит, что алгебраическая сумма зарядов электрически замкнутой системысохраняется.

Закон сохранения заряда выполняется абсолютно точно. На данный момент его происхождение объясняют следствием принципакалибровочной инвариантности^[1][2]. Требование релятивистской инвариантности приводит к тому, что закон сохранения заряда имеетлокальный характер: изменение заряда в любом наперёд заданном объёме равно потоку заряда через его границу. В изначальной формулировке был бы возможен следующий процесс: заряд исчезает в одной точке пространства и мгновенно возникает в другой. Однако, такой процесс был бы релятивистски неинвариантен: из-за относительности одновременности в некоторых системах отсчёта заряд появился бы в новом месте до того, как исчез в предыдущем, а в некоторых — заряд появился бы в новом месте спустя некоторое время после исчезновения в предыдущем. То есть был бы отрезок времени, в течение которого заряд не сохраняется. Требование локальности позволяет записать закон сохранения заряда в дифференциальной и интегральной форме