Лабораторна робота № 7

Тема: Вивчення миттєвих швидкостей транспортних засобів на стаціонарних постах.

Мета: Навчитись досліджувати миттєві швидкості транспортних засобів у транспортних потоках та, застосовуючи методи теорії ймовірностей, знаходити середньозважені швидкості.

Теоретичні відомості

Основними поняттями теорії ймовірностей є подія і її кількісна характеристика – ймовірність події. Під подією розуміють будь-який факт, який може відбутися або не відбутися у результаті деякого експерименту (досліду, випробування).

Щоб кількісно порівняти між собою події за ступенем можливості, до кожної з них необхідно поставити у відповідності визначене число; із збільшенням величини числа збільшується можливість події.

Частість події (статистична ймовірність події) визначається за формулою

(7.1)

де - кількість появ події;

- загальна кількість проведених досліджень.

Нехай із сукупності однотипних автомобілів у транспортному потоці , що рухаються смугою руху населеного пункту, 12 порушило обмеження швидкісного режиму. У такому випадку частота автомобілів-порушників , а відносна частота або частіть,

.

Частість події носить вибірковий характер і може помітно змінюватись від однієї групи дослідів до іншої. Однак, із збільшенням кількості досліджень вона поступово втрачає свій випадковий характер і проявляє тенденцію до стабілізації, тобто наближується з незначним відхиленням до постійної (середньої) величини.

Число, навколо якого прагне стабілізуватись частість події при необмеженій кількості дослідів, називається ймовірністю події. Тому, для наближеної експериментальної оцінки ймовірності події достатньо обчислити її відносну частоту при великій кількості дослідів.

Частість достовірної події, тобто події, яка обов’язково відбудеться за результатами дослідів, завжди рівна одиниці; частість неможливої події, тобто події, яка не відбудеться за результатами дослідів, завжди рівна нулю. У загальному випадку частість випадкової події змінюється від 0 до 1, тобто .

Різноманітність випадкових величин досить велика, а множина значень, які вони приймають може бути скінченою, парною, непарною. Більше того, ці значення можуть розміщуватись дискретно або суцільно заповнювати інтервал часової прямої.

Універсальною характеристикою будь-яких випадкових величин є функція розподілу випадкової величини.

Нехай - випадкова величина і - довільне дійсне число. Функція 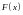дійсної змінної рівна ймовірності того, що , називається функцією розподілу ймовірності випадкової величини :

(7.2)

Випадкові величини позначають великими літерами латинської абетки , а їх можливі значення малими літерами. Для позначення ймовірності події зазвичай використовують латинські літери або .

Таким чином, випадковою величиною називається змінна величина, значення якої залежать від випадкових обставин і для якої визначена функція розподілу ймовірностей.

Дискретна випадкова величина – це випадкова величина, яка може приймати кінцеву або численну величину можливих значень. Наприклад, величина швидкості автомобілів транспортного потоку у населеному пункті може вважатися дискретною випадковою величиною, оскільки діє обмеження швидкісного режиму.

Ряд розподілу дискретних випадкових величин можна також представляти графічно. Всі можливі значення випадкової величини відкладаються на осі абсцис, а ймовірності, що відповідають їм – на осі ординат.

Значення ймовірностей 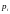часто можна задати одною формулою для всіх . Найбільш відомі закони розподілу:

• біномінальний, для якого можливі значення випадкової величини – цілі числа , ;

, де (7.3)

• пуассонівський, для якого можливі значення – всі невід’ємні цілі числа , причому

, де (7.4)

• геометричний – із цією ж множиною можливих значень і

, де (7.5)

Зазначимо, що кількість успіхів (появи об’єкту, який досліджується) в незалежних дослідах з ймовірністю успіху в окремому досліді має біномінальний розподіл; якщо ж , , , то в межі дане число розподілене за пуассонівський розподілом.

Неперервна випадкова величина може приймати незчисленну множину можливих значень, які суцільно заповнюють деякий проміжок, і подати їх у вигляді будь-якої таблиці абсолютно неможливо. Не дивлячись на це, різні інтервали можливих значень випадкової величини є неоднаково ймовірними, і неперервна випадкова величина характеризується розподілом не конкретних значень, а величин інтервалів.

Із наведеного визначення слідує, що неперервний розподіл характеризується щільністю ймовірності, або диференціальним законом розподілу випадкової величини.

Щільність імовірності неперервної випадкової величини (швидкість) в точці рівна межі відношення імовірності попадання цієї випадкової величини на елементарну ділянку від до до довжини цієї ділянки , коли прямує до 0.

(7.6)

Відповідно, щільність імовірності вказує на те, як часто появляється випадкова величина біля точки при багатократному повторенні досліду. Крива, яка відображає щільність імовірності випадкової величини називається кривою розподілу (рис. 7.1).

При розв’язанні багатьох практичних завдань часто достатньо вказати лише окремі числові параметри, які характеризують суттєві особливості того або іншого розподілу. Це, передусім, деяке середнє значення, около якого групуються можливі значення даної випадкової величини, а також ступінь розкиду цих значень відносно середнього.

У даній лабораторній роботі розглядаємо дискретні величини, відповідно на їх описі і зосередимо нашу увагу.

Перша із вказаних характеристик, що визначає положення випадкової величини на числовій осі, називається математичним очікуванням (середнім значенням) випадкової величини. Для дискретної випадкової величини , що приймає можливі значення , , …, ,… із ймовірностями , ,… ,…,

(7.7)

Наприклад, на перегоні міської вулиці під час досліджень встановлено, що всі швидкості легкових автомобілів приймали значення около чотирьох значень: 46, 52, 43 та 45 км/год. Зі 100 замірів, перше постерігалось у 15 випадках, друге – 50 випадках, третє – 15 випадках, четверте – 20 випадках. Для даного спостереження математичне очікування розрахується:

км/год

Відповідно, математичним очікуванням дискретної випадкової величини називається сума добутків всіх можливих значень випадкової величини на ймовірність цих значень.

Дисперсією випадкової величини називається математичне очікування квадрату відхилення величини від її математичного очікування, тобто

(7.8)

Дисперсія дискретної випадкової величини виражається формулою

(7.9)

На практиці часто використовується інша числова характеристика випадкової величини – середнє квадратичне відхилення, що представляє собою позитивний квадратний корінь з її дисперсії:

(7.10)

Якщо припустити, що X – випадкова величина (миттєва швидкість), яка приймає значення з імовірністю , то будь яка функція від цих імовірностей буде називатись теоретичною характеристикою випадкової величини. Якщо замість в цю функцію підставити частість подій , одержимо емпіричну характеристику. Емпіричні характеристики позначаються тими ж символами, що і теоретичні, але із зірочкою зверху.

Емпіричне середнє:

, (7.11)

де - частота значень при n спостереженнях X; - результат і-го спостереження, при сходяться до .

Емпірична дисперсія

(7.12)

Відомо, що частості випадкових величин прямують до ймовірностей цих величин при необмеженій кількості дослідів . Тому емпіричні характеристики випадкових величин при необмеженому збільшення співпадають з теоретичними.