- •41) Методы вычисления определенного интеграла
- •42) Приложения определенного интеграла: Вычисление площади плоской фигуры, объема тела вращения, длины кривой.
- •43) Несобственные интегралы.
- •44) Двойные интегралы, определение, вычисление.
- •Замена переменных в двойном интеграле.
- •Тройные интегралы, определение, вычисление
- •Замена переменных в тройном интеграле
- •48) Применение кратных интегралов к вычислению площадей, объемов.
- •49) Криволинейные интегралы 1 и 2 рода. Определение, вычисление.
- •50) Формула Грина.
- •51) Дифференциальные уравнения 1-го порядка, задача Коши
Замена переменных в тройном интеграле
Для тройного интеграла имеет место следующее правило замены переменных.
Если
функция ![]() непрерывна
в замкнутой области V, а функции
непрерывна
в замкнутой области V, а функции
![]()
![]()
![]() (1)
(1)
имеют непрерывные частные производные в замкнутой области Т пространства UVW и взаимно однозначно отображают эту область на область V пространства XYZ, то имеет место следующая формула:
![]()
![]() (2)
(2)
где 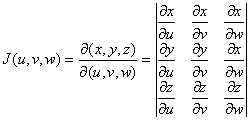 -
якобиан отображения (1).
-
якобиан отображения (1).
Подобно тому как в случае двух переменных модуль якобиана отображения равнялся коэффициенту изменения бесконечно малой площади, модуль якобиана отображения (1) равен коэффициенту изменения бесконечно малого объема при отображении (1).
48) Применение кратных интегралов к вычислению площадей, объемов.
Площадь S, показанная на рисунке может быть вычислена с помощью двойного интеграла по формуле:
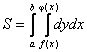
Объем
V = 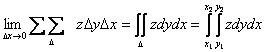
49) Криволинейные интегралы 1 и 2 рода. Определение, вычисление.
Криволинейные интегралы первого рода |
|
|
|
Определение Пусть
кривая C описывается
векторной функцией
Криволинейный
интеграл
|
Свойства криволинейного интеграла первого рода
Криволинейный интеграл I рода обладает следующими свойствами:
Интеграл не зависит от ориентации кривой;
Пусть кривая C1 начинается в точке A и заканчивается в точке B, а кривая C2 начинается в точкеB и заканчивается в точке D (рисунок 2). Тогда их объединением будет называться криваяC1 U C2, которая проходит от A к B вдоль кривой C1 и затем от B к D вдоль кривой C2. Для криволинейных интегралов первого рода справедливо соотношение
![]()
Если гладкая кривая C задана параметрически соотношением
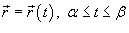 и
скалярная функция F непрерывна
на кривой C,
то
и
скалярная функция F непрерывна
на кривой C,
то
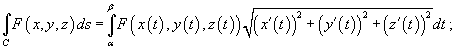
Если C является гладкой кривой в плоскости Oxy, заданной уравнением
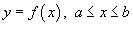 ,
то
,
то
![]()
Если гладкая кривая C в плоскости Oxy определена уравнением
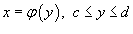 ,
то
,
то
![]()
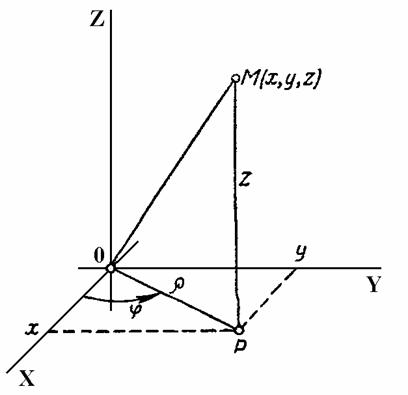
В полярных координатах интеграл
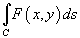 выражается
формулой
выражается
формулой
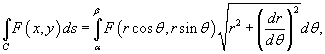
где
кривая C задана
в полярных координатах функцией ![]() .
.
Криволинейные интегралы второго рода |
|
|
|
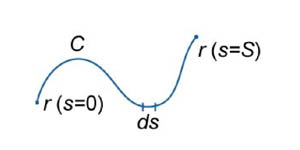
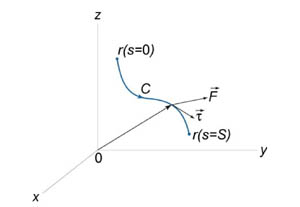
Определение Предположим, что кривая C задана векторной функцией , где переменная s − длина дуги кривой. Тогда производная векторной функции
представляет собой единичный вектор, направленный вдоль касательной к данной кривой (рисунок 1). В приведенной выше формуле α, β и γ − углы между касательной и положительными направлениями осейOx, Oy и Oz, соответственно.
|
Свойства криволинейного интеграла второго рода
Криволинейный интеграл II рода обладает следующими свойствами:
Пусть C обозначает кривую с началом в точке A и конечной точкой B. Обозначим через −Cкривую противоположного направления - от B к A. Тогда
![]()
Если C − объединение кривых C1 и C2 (рисунок 2 выше), то
![]()
Если кривая C задана параметрически в виде
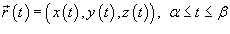 ,
то
,
то
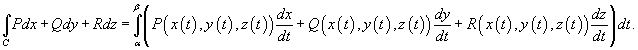
Если кривая C лежит в плоскости Oxy и задана уравнением
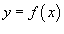 (предполагается,
что R
=0и t
= x),
то последняя формула записывается в
виде
(предполагается,
что R
=0и t
= x),
то последняя формула записывается в
виде
![]()

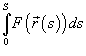 называется криволинейным
интегралом первого рода от
скалярной функции F вдоль
кривой C и
обозначается как
называется криволинейным
интегралом первого рода от
скалярной функции F вдоль
кривой C и
обозначается как