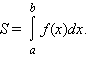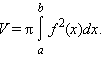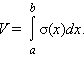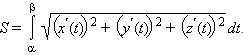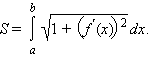41) Методы вычисления определенного интеграла

По Частям

.(7.8)

Метод интегрирования по частям заключается в следующем. Предложенный к вычислению неопределенный интеграл   мы приводим к виду  , причем так, чтобы по выражению   мы смогли най­ти первообразную функцию v (т.е. смогли бы проинтегрировать выражение dv); заметим, что здесь нам достаточно найти какую-нибудь одну из первообразных.

После этого применяем к нашему интегралу   формулу (7.8) в предположении, что вычисление интеграла   окажется проще, чем вычисление интеграла  , или что   окажется подобным интег­ралу   (с коэффициентом, отличным от единицы). Заметим при этом, что для получения окончательного результата может иной раз потребоваться применение метода интегрирования по частям последовательно несколько раз.

Подстановкой

Метод заключается в преобразовании аргумента подынтегральной функции по не­которой формуле, рассчитанной на то, чтобы интеграл в новой переменной оказался проще для вычисления. Например, при вычислении интеграла 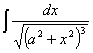 целесообразно  применить  подстановку  , так как тогда   интеграл в новой перемен­ной t оказывается табличным:

.

Ниже будет доказано, что новый интеграл равен старому; тогда

.

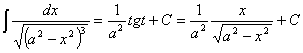Итак, пусть для вычисления неопределенного интеграла   от непрерывной функции f{x) произведена подстановка:  , где функция   монотонная и имеет непрерывную производную; обозначим через   обратную функцию, существование и непрерывность которой следуют из предположенной нами монотонности и непрерывности подстановочной функции  . В силу нашей подстановки  ,  . Заме­няя f(x) и dx их новыми выражениями, мы приводим исходный интеграл к виду  , где   есть непрерывная функция аргумента t.

Докажем, что новый интеграл будет равен исходному:

t.                                  (7.9)

Для этого нам достаточно будет доказать совпадение дифференциалов от левой и от правой части равенства (7.9) при  , или, что то же, при  . Имеем

, 

42) Приложения определенного интеграла: Вычисление площади плоской фигуры, объема тела вращения, длины кривой.

Площадь криволинейной трапеции, ограниченной неотрицательной функцией f (x), осью абсцисс и прямыми x = a, x = b, определяется как 

Объем тела вращения

Пусть тело образовано вращением вокруг оси OX криволинейной трапеции, ограниченной непрерывной на отрезке [a; b] функцией f (x). Его объем выражается формулой 

Пусть тело заключено между плоскостями x = a и x = b, а площадь его сечения плоскостью, проходящей через точку x, – непрерывная на отрезке [a; b] функция σ (x). Тогда его объем равен 

Длина Кривой

Пусть задана кривая    Тогда длина ее участка, ограниченного значениями t = α и t = β выражается формулой 

В частности, длина плоской кривой, задаваемой на координатной плоскости OXY уравнением y = f (x), a ≤ x ≤ b, выражается формулой