
Тема 1.1. Особые случаи при решении задач линейного программирования:
1. Неограниченность задачи.
Признак
неограниченности задачи:
Если существует такое k,
что
 в z-строке
и
в z-строке
и
 для всех i
в соответствующем столбце симплекс-таблицы,
то задача неограниченна.
для всех i
в соответствующем столбце симплекс-таблицы,
то задача неограниченна.
Пусть
k
номер столбца, β
– текущий базис, тогда
 ,
так как таблица описывает результат
приведения задачи к текущему базису.
,
так как таблица описывает результат
приведения задачи к текущему базису.
Выделим слагаемое с номером k в ограничениях и ЦФ:


Определим
вектор
 следующим образом:
следующим образом:
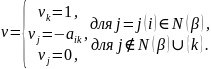
Пусть
X
– множество допустимых решений задачи,
а
 – текущее базисное решение; рассмотрим
луч
– текущее базисное решение; рассмотрим
луч
 .
.
Для
любого
 план
план
 :
:

Для целевой функции получаем:

при
 ,
так как
.
,
так как
.
Получаем,
что для плана
 «надбавка» v
к плану
«надбавка» v
к плану
 реализуется без дополнительных ресурсных
затрат, что невозможно.
реализуется без дополнительных ресурсных
затрат, что невозможно.
Получаем – необходимо изменение исходных данных с целью устранения данной ошибки.
2. Несовместность задачи.
Рассматривается задача в стандартной форме
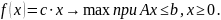
Здесь столбцы aj матрицы A описывают технологические способы, элементы вектора b – запас ресурсов или обязательство (цели) по их производству.
В данной формулировке несовместность задачи означает, что применяемые в модели технологии при имеющихся ресурсах не обеспечивают выполнение обязательств и достижение целей.
Так как реальная система как то работает, то несовместность задачи показывает, что проект (модель) нуждается в доработке.
Направления совершенствования модели:


Изменяем правые части ограничений задачи:
Насколько нужно увеличить каждое bi, чтобы задача стала разрешимой.
Вводим
вектор переменных «надбавок»
 .
.


где ri ≥ 0 – «стоимость» изменения правой части.
Важно: «стоимость» должна быть соизмеримой с исходной целевой функцией.
Пусть
есть ki
способов увеличения bi.
При этом способ k
может увеличить bi
не более чем на
 с удельными затратами
с удельными затратами
 .
Также пусть более дешевые способы имеют
меньшие номера:
.
Также пусть более дешевые способы имеют
меньшие номера:

Задача запишется следующим образом:



Утверждение: Если в оптимальном решении последней задачи zik > 0, то zik` = dik` для всех k` < k (способ применяется только после того, как исчерпаны возможности более дешевых способов).
Доказательство: Пусть в оптимальном решении задачи для некоторых k` < k имеем zik > 0, и zik` < dik`. Тогда существует такое δ >0, что zik – δ > 0 и zik` + δ < dik`. Заменяя в условиях задачи zik на zik – δ, а zik` на zik` + δ, видим, что все они выполняются. Но при этом значение целевой функции выросло на величину δ(rik – rik`) . А это противоречит оптимальности решения.
В некотором роде рассмотренные способы изменения правых частей сводятся к задаче добавления нового технологического способа производства.
Возникает вопрос: каким условиям должен соответствовать технологический способ, добавляемый в модель с целью устранения несовместности?
Рассматривается задача P в канонической форме:
c · x → max при Ax = b, x ≥ 0.
Будем считать, что вектор b ≥ 0.
Решение данной задачи происходит с симплекс-метода, с поиска исходного БДР методом искусственного базиса: рассматривается вспомогательная задача P1, которая всегда разрешима:
– Σi ti → max при Ax + t = b, x ≥ 0, t ≥ 0.
Пусть f1 – оптимальное решение задачи P1. | f1| указывает на минимальную достижимую величину «суммарного невыполнения» ограничений задачи P. Если задача P совместна, то f1 = 0 , иначе f1 < 0.
Устранение несовместности задачи – введение такого технологического способа, который повысит значение f1 (в идеале до нуля).
Рассмотрим задачу P1* , двойственную к вспомогательной:
h(y) = b · y → min при yA ≥ 0, yi ≥ –1 для всех i.
Так как задача P1 разрешима, то и двойственная к ней будет иметь решение y* и h(y*) = f1.
Предположим, что в исходную задачу вводится новый технологический способ: переменная x ≥ 0 с коэффициентами ai в ограничениях и c – в целевой функции. Аналогично строится вспомогательная задача P2.
Она будет отличаться от P1 введенной дополнительной переменной с теми же коэффициентами в ограничениях и нулевым коэффициентом в ЦФ.
Пусть x допустимое решение задачи P1, тогда решение (x, x) при x = 0 – допустимо в P2. Задача P2 совместна. Двойственная к ней P2* – также разрешима.
Отличие задачи P2* от задачи P1* в ограничении:
Σi aiyi ≥ 0 (*).
Задачи P2 и P2* разрешимы одновременно по первой теореме двойственности. Их целевые функции имеют одинаковые значения f2.
Пусть
Y1
и Y2
– множества допустимых решений задач
P1*
и P2*
соответственно. Поскольку любое
дополнительное ограничение сужает
область поиска решения, то Y1
 Y2.Поэтому
f1
≤
f2
– чем шире области минимизации (Y1),
тем меньше минимум.
Y2.Поэтому
f1
≤
f2
– чем шире области минимизации (Y1),
тем меньше минимум.
Если
решение задачи P1*
удовлетворяет условию (*), то оно также
является допустимым решением задачи
P2*:
y*
 Y2
и f2
= minY2
h(y)
≤ h(y*)
= f1
Y2
и f2
= minY2
h(y)
≤ h(y*)
= f1
Так как нам нужно, чтобы при добавлении способа значение целевой функции задачи P1 повышалось (f1 <f2), то, c учетом вышеупомянутого замечания, необходимо, чтобы условие (*) не выполнялось.
Утверждение: Для того, чтобы в несовместной задаче P с неотрицательным вектором b после введения нового технологического способа (a1,…,am, c) задача стала совместной, коэффициенты ai должны удовлетворять условию
Σi aiyi* < 0,
где yi* – двойственные оценки вспомогательной задачи P1.
Замечание: Указанное в утверждении условие необходимо, но, вообще говоря, недостаточно, чтобы при введении нового технологического способа задача стала совместной (потребуется введение нескольких дополнительных технологических способов).
