
- •1. Выборочный метод в системе статистического обследования.
- •1. Понятие и сущность выборочного наблюдения
- •3. Инструменты выборочного обследования.
- •5. Преимущество выборочного метода перед сплошным наблюдением.
- •2. Теоретические основы применения выборочного метода.
- •1. Основные законы случая и их роль в выборочных наблюдениях
- •2. Средняя и предельная ошибки выборки. Теоремы Чебышева и Ляпунова
- •3. Теорема Бернулли. Уточнение формулы средней ошибки выборки
- •3. Подготовка и организация выборочного обследования.
- •2. Программа проведения выборочного обследования
- •3. Разработка формуляр выборочного обследования
- •2. Построение основы выборки
- •4. Определение объема выборки.
- •1. Основные этапы определения объема выборки
- •2. Определение объема выборки в случае непрерывных переменных
- •3. Определение объема выборки при оценивании долей и процентов
- •5. Простой случайный отбор.
- •1. Формирование простой случайной выборки
- •2. Параметры выборочной совокупности
- •6. Расслоенный случайный отбор.
5. Преимущество выборочного метода перед сплошным наблюдением.
Выборочный метод по сравнению со сплошным наблюдением имеет следующие преимущества:
1) Меньшая стоимость мероприятий, проводимых в рамках обследования. Затраты на получение данных лишь относительно небольшой части всей совокупности намного меньше чем при сплошном наблюдении.
2) Более короткие сроки реализации мероприятий. Так как обследуется только часть совокупности, то данные выборочного обследования можно собрать и обобщить быстрее, чем при сплошном наблюдении.
3) Более широкая область применения. При некоторых видах обследования для сбора данных требуется привлечение более квалифицированного персонала или необходимо воспользоваться специальным оборудованием, как правило, и то и другое ограничено.
4) Большая достоверность. Если общий объем работы при выборочном обследовании достаточно большой, то можно привлечь более квалифицированный персонал, лучше его подготовить, более тщательно контролировать проведение, а так же обработку его результатов, поэтому выборочное обследование может дать более достоверные сведения, чем сплошное наблюдение.
2. Теоретические основы применения выборочного метода.
Закон больших чисел и закон распределения вероятностей, их роль в выборочных наблюдениях. Теоремы Чебышева и Ляпунова как основа оценки средней и предельной ошибок выборки. Теорема Бернулли: уточнение формулы средней ошибки выборки.
1. Основные законы случая и их роль в выборочных наблюдениях
Основным из законов случая, исследованием которого занимается теория вероятностей, является закон больших чисел (далее ЗБЧ). Что касается практики выборочного обследования, то действие ЗБЧ проявляется в нем в уменьшении величины случайной ошибки при увеличении численности выборки. Это позволяет с большей вероятностью указывать более узкие границы доверительного интервала, в котором может находиться неизвестная характеристика генеральной совокупности. Вместе с ЗБЧ основополагающее значение для вероятности оценки статистических результатов выборочного наблюдения имеет закон распределения вероятности. Согласно закону нормального распределения кривая нормального распределения при сравнительно небольшом числе наблюдений может служить хорошей аппроксимацией биномиального распределения*.
Для того, что бы законы случая могли проявиться, необходимо создать некоторые благоприятные для этого условия. При статистическом наблюдении такие условия создает случайный отбор.
Случайную выборку можно получить только при соблюдении определенной методики обеспечивающей случайность отбора (например, извлечение жребия или применение таблицы случайных чисел) но их можно использовать только в том случае, если исходная совокупность конечна и сравнительно не велика, так как оба метода предусматривают нумерацию единиц совокупности.
2. Средняя и предельная ошибки выборки. Теоремы Чебышева и Ляпунова
В процессе проведения выборочного наблюдения, как и при любом другом анализе статистических данных любого обследования, могут возникать два вида ошибок: регистрации и репрезентативности. Ошибки регистрации могут иметь случайный (непреднамеренный) или систематический (тенденциозный) характер. Их можно избежать при правильной организации и проведении наблюдения. Ошибки репрезентативности изначально присущи выборочному наблюдению и возникают в силу того, что выборочная совокупность не полностью воспроизводит генеральную. Избежать ошибок репрезентативности нельзя, однако, пользуясь методами теории вероятностей, основанными на использовании предельных теорем закона больших чисел, эти ошибки можно свести к минимальным значениям, границы которых устанавливаются с достаточно большой точностью.
Так ошибкой выборочного наблюдения имеет смысл считать разность между величиной параметра в генеральной совокупности и его величиной, вычисленной по результатам выборочного наблюдения. Для среднего значения ошибка будет определяться так:
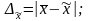 (1)
(1)
где
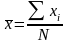 – генеральная средняя;
– генеральная средняя;
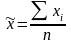 – выборочная
средняя;
– выборочная
средняя;
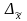 – предельная
ошибка выборки.
– предельная
ошибка выборки.
Предельная ошибка выборки по своей природе является случайной величиной. Исследованию закономерностей случайных ошибок посвящены предельные теоремы закона больших чисел. Наиболее популярно и достаточно просто эти закономерности раскрыты в теоремах Пафнутия Львовича Чебышева и Александра Михайловича Ляпунова.
Теорему Чебышева применительно методу выборочных обследований можно сформулировать следующим образом: при достаточно большом числе независимых наблюдений можно с вероятностью, близкой к единице (т.е. почти с полной достоверностью) утверждать что отклонение выборочной средней от генеральной будет сколь угодно малым. В теореме Чебышева доказано, что величина ошибки не должна превышать tμ. В свою очередь, величина μ, выражающее среднее квадратическое отклонение выборочной средней от генеральной средней, зависит от колеблемости признака в генеральной совокупности σ и числа отобранных единиц n. Эта зависимость выражается формулой:
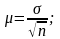 (2)
(2)
где μ зависит также и от способа формирования выборочной совокупности, о чем сказано ниже.
Величину
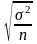 называют средней
ошибкой выборки.
называют средней
ошибкой выборки.
В этом выражении σ2 – генеральная дисперсия, а n – объем выборочной совокупности.
Соотношение между дисперсиями генеральной и выборочной совокупности выражается формулой:
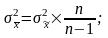 (3)
(3)
Поскольку
величина
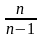 при достаточно больших n
близка к 1, можно приближенно считать,
что выборочная дисперсия равна
генеральной, т.е.
при достаточно больших n
близка к 1, можно приближенно считать,
что выборочная дисперсия равна
генеральной, т.е.
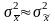 .
.
Следовательно, средняя ошибка выборки показывает, какие возможны отклонения характеристик выборочной совокупности от соответствующих характеристик генеральной совокупности. Однако о величине этой ошибки можно судить с определенной вероятностью. На величину вероятности указывает множитель t.
В теореме Ляпунова доказывается, что распределение выборочных средних (а, следовательно, и их отклонений от генеральной средней) при достаточно большом числе независимых наблюдений приближенно нормально при условии, что генеральная совокупность обладает конечной средней и ограниченной дисперсией.
Математически теорему Ляпунова можно записать так:
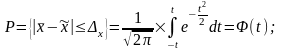 (4)
(4)
где
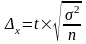 – предельная
ошибка выборки,
которая дает возможность выяснить, в
каких пределах находится величина
генеральной средней.
– предельная
ошибка выборки,
которая дает возможность выяснить, в
каких пределах находится величина
генеральной средней.
Значения указанного интеграла для различных значений коэффициента t вычислены и приводятся в специальных математических таблицах. В частности, при:
t = 1 Φ(t) = 0,683;
t = 1,5 Φ(t) = 0,866;
t = 2 Φ(t) = 0,954;
t = 2,5 Φ(t) = 0,988;
t = 3 Φ(t) = 0,997;
t = 3,5 Φ(t) = 0,999.
Поскольку
t
указывает
на вероятность расхождения тождества
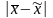 ,
т.е. на вероятность того, на какую величину
генеральная средняя будет отличаться
от выборочной средней, то это может быть
прочитано так: с вероятностью 0,683 можно
утверждать, что разность между выборочной
и генеральной средними не превышает
одной величины средней ошибки выборки.
Другими словами, в 68,3% случаев ошибка
репрезентативности не выйдет за пределы
± μ.
С вероятностью 0,954 можно утверждать,
что ошибка репрезентативности не
превышает ± 2μ
(т.е. в 95% случаев). С вероятностью 0,997,
т.е. довольно близкой к единице, можно
ожидать, что разность между выборочной
и генеральной средней не превзойдет
трехкратной средней ошибки выборки и
т.д.
,
т.е. на вероятность того, на какую величину
генеральная средняя будет отличаться
от выборочной средней, то это может быть
прочитано так: с вероятностью 0,683 можно
утверждать, что разность между выборочной
и генеральной средними не превышает
одной величины средней ошибки выборки.
Другими словами, в 68,3% случаев ошибка
репрезентативности не выйдет за пределы
± μ.
С вероятностью 0,954 можно утверждать,
что ошибка репрезентативности не
превышает ± 2μ
(т.е. в 95% случаев). С вероятностью 0,997,
т.е. довольно близкой к единице, можно
ожидать, что разность между выборочной
и генеральной средней не превзойдет
трехкратной средней ошибки выборки и
т.д.
Логическая связь здесь выглядит довольно ясно: чем больше пределы, в которых допускается возможная ошибка, тем с большей вероятностью судят о ее величине.
