18) Сформулировать свойство инвариантности характеристического уравнения линейного оператора

Характеристическим многочленом линейного оператора A: L → L называют характеристический многочлен его матрицы A, записанной в некотором базисе, а характеристическим уравнением этого оператора — характеристическое уравнение матрицы A.

Определение корректно, так как характеристический многочлен не зависит от выбора базиса. При этом коэффициенты 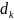характеристического многочлена, представленного в виде

= det(A − λE) = также не связаны с используемым базисом, т.е. являются инвариантами относительно выбора базиса. Другими словами, коэффициенты отражают свойства самого оператора, а не его матрицы A, являющейся записью оператора в конкретном базисе.

19) ДАТЬ ОПРЕДЕЛЕНИЕ СЛЕДА МАТРИЦЫ

След матрицы — операция, отображающая пространство квадратных матриц в поле, над которым определена матрица. След матрицы — это сумма элементов главной диагонали матрицы, то есть если   элементы матрицы  , то её след  .

20)СФОРМУЛИРОВАТЬ СВОЙСТВО ИНВАРИАНТНОСТИ СЛЕДА МАТРИЦЫ ЛИНЕЙНОГО ОПЕРАТОРА

Чтобы установить инвариантность следа, докажем общий факт: если A,B – такие матрицы, что AB и BA определены, то TrAB=TrBA

Действительно,

Если теперь B невырождена, получим

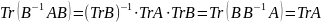
21)СФОРМУЛИРОВАТЬ ОПРЕДЕЛЕНИЯ СОБСТВЕННОГО ЗНАЧЕНИЯ И СОБСТВЕННОГО ВЕКТОРА ЛИНЕЙНОГО ОПЕРАТОРА

Ненулевой вектор x в линейном пространстве L называют собственным вектором линейного оператора A:L→L ,если для некоторого действительного числа λ выполняется соотношение Ax= λx. При этом число λ называют собственным значением линейного оператора A.

22)ДАТЬ ОПРЕДЕЛЕНИЕ СОБСТВЕННОГО ПОДПРОСТРАНСТВА ЛИНЕЙНОГО ОПЕРАТОРА,ОТВЕЧАЮЩЕГО ДАННОМУ СОБСТВЕННОМУ ЗНАЧЕНИЮ

Собственным подпространством линейного преобразования   для данного собственного числа   называется множество всех собственных векторов  , соответствующих данному собственному числу (дополненное нулевым вектором). Обозначим его  . По определению,

,где   — единичный оператор.

23)СФОРМУЛИРОВАТЬ ТЕОРЕМУ О СОБСТВЕННЫХ ВЕКТОРАХ ЛИНЕЙНОГО ОПЕРАТОРА,СООТВЕТСТВУЮЩИХ РАЗЛИЧНЫМ СОБСТВЕННЫМ ЗНАЧЕНИЯМ

Собственные векторы, отвечающие различным собственным значениям, линейно независимы.

24)СФОРМУЛИРОВАТЬ ТЕОРЕМУ О МАТРИЦЕ ЛИНЕЙНОГО ОПЕРАТОРА В БАЗИСЕ ИЗ СОБСТВЕННЫХ ВЕКТОРОВ

Если линейный оператор имеет собственный базис, то матрица оператора в собственном базисе имеет диагональный вид; диагональными элементами являются собственные значения оператора.

/*Матрица линейного оператора имеет диагональную форму тогда и только тогда, когда она записана в базисе, составленном из собственных векторов*/

25)СФОРМУЛИРОВАТЬ ОПРЕДЕЛЕНИЕ СОПРЯЖЕННОГО ЛИНЕЙНОГО ОПЕРАТОРА

Если существует такой оператор B, что для любых и из Rn справедливо ,

то оператор B называется сопряженным оператором к оператору A и обозначается A*:

(важно)( для Rn должно быть определено скалярное произведение векторов: , тоесть оно должно быть например Евклидовым)

26) СФОРМУЛИРОВАТЬ ОПРЕДЕЛЕНИЕ САМОСОПРЯЖЕННОГО ЛИНЕЙНОГО ОПЕРАТОРА

Если для любых и из Rn справедливо , то оператор A называется самосопряженным оператором.

27)СФОРМУЛИРОВАТЬ ТЕОРЕМУ О ВИДЕ МАТРИЦЫ САМОСОПРЯЖЕННОГО ОПЕРАТОРА В ОРТОНОРМИРОВАННОМ БАЗИСЕ

Матрица самосопряженного оператора в любом ортонормированном базисе является симметричной.

И наоборот: если матрица линейного оператора в некотором ортонормированном базисе является симметричyой, то этот оператор — самосопряженный.

28)СФОРМУЛИРОВАТЬ ТЕОРЕМУ О КОРНЯХ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ САМОСОПРЯЖЕННОГО ОПЕРАТОРА

Все корни характеристического уравнения самосопряженного оператора действительны.

Следствия(не уверен, что надо, но пусть будут):

1. Если матрица A является симметрической, то все корни ее характеристического уравнения det(A − λE) = 0 действительные.

2. Самосопряженный оператор, действующий в n-мерном евклидовом про- странстве, имеет n собственных значений, если каждое из них считать столько раз, какова его кратность.

3. Симметрическая матрица порядка n имеет n собственных значений, если каждое из них считать столько раз, какова его кратность.