Контрольные вопросы

1. Сколько ячеек должно быть на карте Карно для функции пяти переменных?

2. Можно ли найти минимальную форму записи логической функции с помощью метода Квайна?

3. Можно ли приступить к кодированию нулями и единицами (метод Квайна – Мак-Класки) следующей формы записи логической функции?

4. Обязательно ли включать в контуры ячейки с прочерками при минимизации неполностью определенных логических функций?

5. Для какой из функций: или необходимо найти сокращенную нормальную форму при минимизации неполностью определенных логических функций?

9. Свойства логических функций

Функция f(x₁, x₂, ..., x_i–1, x_i, x_i+1, ..., x_n) называется существенно зависящей от аргумента x_i, если хотя бы на одном наборе входных переменных

f(x₁, x₂, ..., x_i–1, 0, x_i+1, ..., x_n)  f(x₁, x₂, ..., x_i–1, 1, x_i+1, ..., x_n)

Функция называется сохраняющей нуль, если она равна нулю на нулевом наборе данных.

f(x₁, x₂, ..., x_n) = 0 при всех x_i = 0, i = 1, 2, ..., n

Функция называется сохраняющей единицу, если она равна единице на единичном наборе данных.

f(x₁, x₂, ..., x_n) = 1 при всех x_i = 1, i = 1, 2, ..., n

Функция называется самодвойственной, если она принимает противоположные значения на противоположных наборах аргументов.

Функция называется монотонной, если выполняется условие

f(x₁, x₂, …, x_n)  f(x₁’, x₂’, …, x_n’) при всех x_i  x_i’, i = 1, 2, ..., n

Замечание: если ни одно из условий x_i  x_i’ для всех i от 1 до n или x_i  x_i’ для всех i от 1 до n не выполняется, то говорят, что наборы x_i и x_i’ несравнимы. Пусть , , . Тогда , а и  , а также и  будут несравнимыми.

Функция называется линейной, если ее можно представить линейным полиномом Жегалкина

,

где a₀, a₁, ..., a_n - константы, которые могут принимать значения 0 и 1.

Пример 1. Определим свойства функции логического умножения И

1. Сохраняет нуль, так как f(0, 0) = 0.

2. Сохраняет единицу, так как f(1, 1) = 1.

3. Не является самодвойственной, так как .

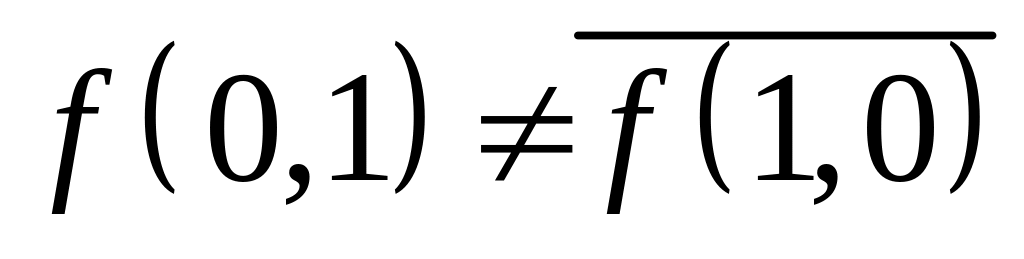4. Монотонна, так как

f(1, 1)   f(0, 1),

f(1, 1)   f(1, 0),

f(1, 1)   f(0, 0),

f(0, 1)   f(0, 0),

f(1, 0)   f(0, 0),

остальные наборы входных переменных несравнимы.

5. f(x₁, x₂) = x₁x₂ не является линейной, так как ее невозможно представить в виде линейного полинома Жегалкина.

Пример 2. Определить свойства логической функции, заданной таблицей

x1	0	0	0	0	1	1	1	1
x2	0	0	1	1	0	0	1	1
x3	0	1	0	1	0	1	0	1
f	0	1	0	1	0	1	0	1

f(0, 0, 0) = f(1, 0, 0)

f(0, 0, 1) = f(1, 0, 1)

f(0, 1, 0) = f(1, 1, 0)

f(0, 1, 1) = f(1, 1, 1)  f не зависит существенно от x₁

f(0, 0, 0) = f(0, 1, 0)

f(0, 0, 1) = f(0, 1, 1)

f(1, 0, 0) = f(1, 1, 0)

f(1, 0, 1) = f(1, 1, 1)  f не зависит существенно от x₂

f(0, 0, 0)  f(0, 0, 1)  f существенно зависит от x₃

f(0, 0, 0) = 0  f сохраняет ноль

f(1, 1, 1) = 1  f сохраняет единицу

f(0, 0, 0)  f(1, 1, 1)

f(0, 0, 1)  f(1, 1, 0)

f(0, 1, 0)  f(1, 0, 1)

f(0, 1, 1)  f(1, 0, 0)  f самодвойственна

f(1, 1, 1) > f(0, 0, 0)

f(1, 1, 0) = f(1, 0, 0)

f(1, 1, 0) = f(0, 1, 0)

f(1, 0, 1) > f(1, 0, 0)

f(1, 0, 1) = f(0, 0, 1)

f(0, 1, 1) > f(0, 1, 0)

f(0, 1, 1) = f(0, 0, 1)  f монотонна

Из таблицы значений функции f понятно, что f = x₃. Эта запись одновременно является и полиномом Жегалкина для функции f. Данный полином – линейный (так как в нем нет слагаемых, являющихся конъюнкциями нескольких переменных), следовательно, и функция f является линейной.

Пример 3. Определить свойства логической функции, заданной таблицей

x	0	0	0	0	1	1	1	1
y	0	0	1	1	0	0	1	1
z	0	1	0	1	0	1	0	1
f	1	1	0	1	0	1	0	1

f(0, 0, 0)  f(1, 0, 0)  f существенно зависит от x

f(0, 0, 0)  f(0, 1, 0)  f существенно зависит от y

f(0, 1, 0)  f(0, 1, 1)  f существенно зависит от z

f(0, 0, 0) = 1  f не сохраняет ноль

f(1, 1, 1) = 1  f сохраняет единицу

f(0, 0, 0) = f(1, 1, 1)  f не является самодвойственной

f(0, 1, 0) < f(0, 0, 0)  f не является монотонной

Получить полином Жегалкина можно из ДСНФ функции. Чтобы упростить данный процесс, попробуем сначала минимизировать нашу функцию, например, с помощью карты Карно.

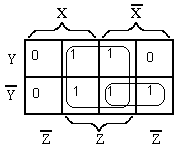
f(x, y, z) = z +xy = z xy xy z = z  (x  1)(y  1)  (x  1)(y  1)z =

= z  xy  x  y  1  xyz  xz  yz  z = xyz  xy  xz  yz  x  y  1

Замечание:

Были использованы следующие преобразования:

a + b = a  b  ab

a = a  1

a  a = 0

a  0 = a

Полученный полином Жегалкина не является линейным, следовательно, исходная функция f – не линейная.