Определения и формулировки теорем по математическому анализу.

2 Семестр.

За корректность приведенных ниже формулировок теорем и определений ответственности не несу

1-4. Определение возрастающей (убывающей) функции

возрастает (убывает) в точке , если существует и .

возрастает (убывает) на множестве , если для .

5-6. Определение выпуклой вверх (вниз) функции

выпукла вверх (вниз) на множестве , если график лежит не выше (не ниже) касательной в каждой точке .

7. Определение точки перегиба функции

Точка называется точкой перегиба, если при прохождении через меняется направление выпуклости графика.

8. Достаточное условие точки перегиба

Пусть имеет вторую производную в некоторой окрестности точки и . Тогда, если в указанной окрестности вторая производная имеет разные знаки слева и справа от , то график функции имеет перегиб в точке .

Если функция имеет в точке конечную третью производную и удовлетворяет в этой точке условию , , то график функции имеет перегиб в точке .

Пусть некоторое четное число и пусть имеет производную порядка в некоторой окрестности точки и производную порядка в самой точке . Тогда если

,

то график функции имеет перегиб в точке .

9. Определение точки экстремума функции одной переменной

- точка локального экстремума функции , если - точка локального максимума или минимума.

10-11. Определение точки локального минимума (максимума) функции одной переменной

имеет в точке локальный максимум (минимум), если .

12. Необходимое условие экстремума функции одной переменной

- дифференцируема в точке , - точка локального экстремума

13. Достаточное условие экстремума функции одной переменной

- дифференцируема, тогда - точка локального экстремума, если при прохождении через нее меняет знак.

- дважды дифференцируема, и в точке локальный минимум (максимум)

Пусть некоторое нечетное число и пусть имеет производную порядка в некоторой окрестности точки и производную порядка в самой точке . Тогда если

,

То в точке локальный максимум, если и минимум, если .

14. Определение интеграла Римана

Функция называется интегрируемой по Риману на , если для этой функции на указанном сегменте существует предел ее интегральных сумм при стремлении диаметра разбиений к нулю.

Число называют определенным интегралом Римана от в пределах от до и обозначают .

15. Определение верхней и нижней интегральных сумм

16. Верхний и нижний интегралы Дарбу

Верхним интегралом Дарбу от называют число , равное точной нижней грани множества верхних сумм для всевозможных разбиений сегмента .

Нижним интегралом Дарбу от называют число , равное точной верхней грани множества нижних сумм для всевозможных разбиений сегмента .

17. Необходимое и достаточное условие интегрируемости функций

Для того чтобы ограниченная на функция была интегрируема на этом сегменте необходимо и достаточно, чтобы .

Для того чтобы ограниченная на функция была интегрируема на этом сегменте необходимо и достаточно, чтобы сегмента , для которого .

18. Классы интегрируемых функций

Непрерывные на функции интегрируемы на этом сегменте по Риману.

Монотонные на интегрируемы на этом сегменте по Риману.

Пусть определена и ограничена на . Если конечное число интервалов покрывающих точки разрыва этой функции и имеющих общую сумму длин меньшую , то интегрируема по Риману на

19. Формула Ньютона-Лейбница.

Пусть непрерывна на

, - первообразная на .

20. Интегрирование по частям

Пусть и имеют непрерывные производные на , тогда

.

21. Интегрирование заменой переменного

Пусть имеет непрерывную производную на и , , причем . Тогда

( при условии, что непрерывна)

22. Определение среднего значения функции

называется средним значением функции на .

23. Теорема о среднем значении непрерывной функции

Если непрерывна на , то .

24. Первая теорема о среднем

- интегрируема

интегрируема

25. Вторая теорема о среднем

-интегрируемы

- монотонная

26. Определение несобственного интеграла первого рода.

Предел в случае, если он существует, называется несобственным интегралом первого рода от по полупрямой и обозначается символом , при этом говорят, что несобственный интеграл сходится и пишут .

27. Определение несобственного интеграла второго рода

Правый предел в случае, если он существует, называется несобственным интегралом второго рода от по и обозначается символом

При этом говорят, что интеграл сходится и пишут .

28. Критерий Коши сходимости интеграла первого рода

Для сходимости интеграла первого рода необходимо и достаточно, чтобы .

29. Критерий Коши рассходимости интеграла первого рода

Для рассходимости интеграла первого рода необходимо и достаточно, чтобы

.

30. Критерий Коши сходимости интеграла второго рода

Для сходимости интеграла второго рода необходимо и достаточно, чтобы

.

31. Критерий Коши рассходимости интеграла второго рода

Для рассходимости интеграла второго рода необходимо и достаточно, чтобы

.

32. Абсолютная и условная сходимость интеграла

при абсолютно сходится

при условно сходится.

33. Абсолютная и условная сходимость интеграла

при абсолютно сходится

при условно сходится.

34. Сходимость интеграла

сходится при .

35. Сходимость интеграла

сходится при .

36. Определение несобственного интеграла в смысле главного значения

Пусть определена на и интегрируема на каждом сегменте принадлежащем этой прямой. Будем говорить, что интегрируема по Коши, если существует предел

Называемый главным значением интеграла в смысле Коши.

37. Определение несобственного интеграла в смысле главного значения

Пусть определена на , быть может кроме точки , , и интегрируема на любом сегменте принадлежащем либо , либо . Будем говорить, что интегрируема по Коши, если существует предел

Называемый главным значением интеграла в смысле Коши.

38. Первый признак сравнения сходимости несобственного интеграл

определены на и , из сходимости сходимость .

Из расходимости расходимость .

39. Второй признак сходимости несобственного интеграла

знакоопределены и

и сходятся и расходятся одновременно.

40. Частный признак сравнения несобственного интеграла

Пусть на полупрямой функция удовлетворяющая соотношению , и постоянные, . Тогда сходится.

Если на справедливо соотношение , то интеграл расходится.

41. Признак Дирихле-Абеля сходимости несобственного интеграла

1. непрерывна на полупрямой и имеет на этой полупрямой ограниченную первообразную

2. - определена и монотонно не возрастает на полупрямой и имеет равный нулю предел при

3. существует и непрерывна в каждой точке полупрямой

Тогда интеграл сходится.

42. Определение абсолютной сходимости несобственного интеграла

Интеграл - сходится - абсолютно сходится.

43. Определения условной сходимости несобственного интеграла

Интеграл -расходится, - сходится условно сходится.

44. Вычисление площади ограниченной замкнутой кривой

Площадь плоской фигуры ограниченной двумя непрерывными кривыми ( и двумя прямыми ( )), равна

.

Если ( ) – параметрические уравнения кусочно гладкой простой замкнутой кривой , пробегаемой против хода часовой стрелки и ограничивающей слева от себя фигуру с площадью , то

.

45. Вычисление площади сектора, ограниченного кривой, в полярных координатах

Площадь сектора сектора ограниченной непрерывной кривой и двумя полупрямыми , равна

46. Вычисление длины дуги кривой в декартовой системе координат

Длина дуги отрезка гладкой (непрерывно дифференцируемой) кривой

равна

Если кривая задана уравнениями , где непрерывно дифференцируемы на , то длина дуги кривой равна

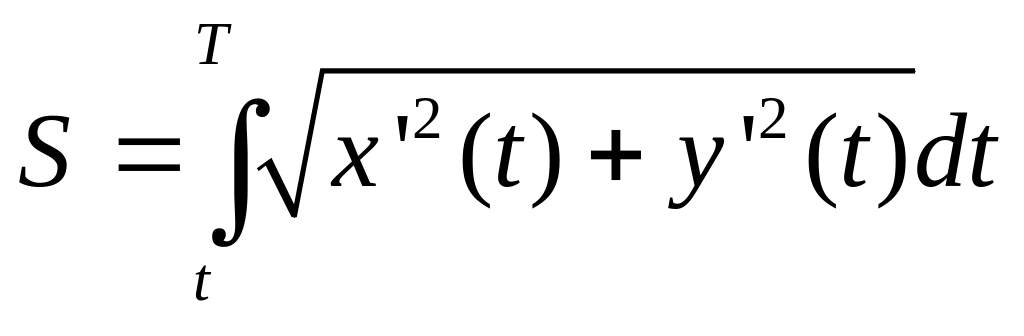
47. Вычисление длины дуги кривой в полярных системе координат

Если ( ) , где непрерывно дифференцируема на , то длина дуги соответствующего отрезка кривой равна

.

48. Вычисление площади поверхности вращения

Площадь поверхности, образованной вращением гладкой кривой вокруг оси , равна

,

где дифференциал дуги

1)

2)

3)

49. Вычисление объема тела вращения

Объем тела, образованного вращением вокруг оси криволинейной трапеции

,

где непрерывная функция, равен

.

50. Сходимость точек в n-мерном пространстве

 

Последовательность точек Евклидова пространства называется сходящейся, если существует точка пространства такая, что для выполняется неравенство . При этом точка называется предельной точкой последовательности .

 

51. Теорема Больцано-Вейерштрассе

 

Из любой ограниченной последовательности точек -мерного евклидова пространства можно выделить сходящуюся подпоследовательность.

52. Определение предела функции многих переменных