
- •Немного теории к коллоквиуму по дискретной математике (не все вопросы!!!)
- •Операции над множествами
- •Виды выборок
- •Теорема 1. Число перестановок без повторений
- •Теорема 2. Число перестановок с повторениями
- •Теорема 3. Число сочетаний без повторений
- •Теорема 4. Число сочетаний с повторениями
- •Лекция 4. Метод включения и исключения. Формула решета
- •Лекция 5. Задача о беспорядках
- •Функция Эйлера
- •Функция Мебиуса
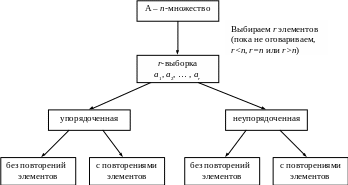
Виды выборок
Комбинаторику интересуют результаты отбора (построения выборок) и упорядочения элементов, выраженные в комбинаторных числах. Если после выбора элемент из множества удаляется (его нельзя еще раз выбрать) – это выборка без повторений. Если после выбора элемент из множества не удаляется и его можно выбрать еще раз – это выборка с повторениями. Если в выборках важен порядок элементов – это перестановки. Если же выборки с разным порядком элементов считаются одинаковыми – это сочетания.
С понятием отбора элементов в комбинаторике связано понятие выборки. Выборки могут быть упорядоченными и неупорядоченными, без повторений элементов и с повторениями.
Обозначим знаком
![]() отношение упорядоченности. Тогда запись
отношение упорядоченности. Тогда запись
![]() означает, что a предшествует b,
а
означает, что a предшествует b,
а
![]() - a предшествует или совпадает с b.
- a предшествует или совпадает с b.
|
|
|
|
r-перестановка без повторений из n-множества
|
r-перестановка c повторениями из n-множества
|
r-сочетание без повторений из n-множества
|
r-сочетание с повторениями из n-множества
|
Теорема 1. Число перестановок без повторений
Число r-перестановок без повторений из элементов n-множества равно
![]() .
.
# Пусть дано n-множество S и Ti – ni-подмножества множества S, где i=1,2,…,n. Тогда доказательство есть частный случай применения обобщенного правила произведения, где
n1=n, n2=n-1, n3=n-2, …, nr=n-r+1 #
Следствие 1. Число перестановок n предметов равно:
![]() .
.
Следствие 2.
![]() .
.
Следствие 3. При r>n
![]() (в перестановках с повторениями r
не может быть больше n, так как мы не
можем из n-множества забрать более,
чем n элементов).
(в перестановках с повторениями r
не может быть больше n, так как мы не
можем из n-множества забрать более,
чем n элементов).
По определению,
![]() (ноль предметов можно выбрать из n
предметов единственным способом –
ничего не выбирать).
(ноль предметов можно выбрать из n
предметов единственным способом –
ничего не выбирать).
Выборка. Виды выборок. Примеры. Упорядоченные выборки. Теоремы о числе упорядоченных выборок с повторениями. Доказательства.
Следствия.
Теорема 2. Число перестановок с повторениями
Число r-перестановок с повторениями
из n-множества равно
![]() .
.
# Следует из обобщённого правила произведения, где n1=n, n2=n, n3=n, …, nr=n. (Выбираем из исходного множества какой-либо элемент, ставим его на очередное место в перестановке, но из исходного множества не удаляем и его можно будет выбрать ещё раз) #
В перестановках с повторениями r может быть больше n, так как при выборе элемента мы не удаляем его из множества и можем выбрать еще раз.
Выборка. Виды выборок. Примеры. Неупорядоченные выборки. Теоремы о числе неупорядоченных выборок без повторений. Доказательства. Следствия.
Теорема 3. Число сочетаний без повторений
Число r-сочетаний без повторений из n-множества равно
![]() .
.
# Число r-перестановок без повторений
из n-множества равно
,
однако порядок элементов в r‑выборке
здесь нас не интересует. Число возможных
перестановок элементов в r-выборке
равно
![]() .
Следовательно, число сочетаний без
повторений в r! раз меньше числа
перестановок без повторений.
.
Следовательно, число сочетаний без
повторений в r! раз меньше числа
перестановок без повторений.
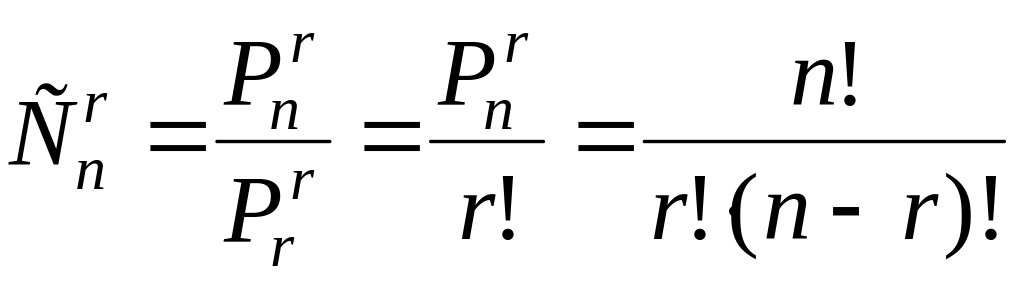 #
#
Следствие 1.
Свойство симметричности для числа
сочетаний без повторений:
![]() .
.
#
![]() #
#
Следствие 2.
![]() ,
т.к.
,
т.к.
![]() (Ноль предметов выбрать из n предметов
можно единственным способом – ничего
не выбирать. Выбрать n предметов из n без
учета порядка можно единственным
способом – выбрать все n предметов.)
(Ноль предметов выбрать из n предметов
можно единственным способом – ничего
не выбирать. Выбрать n предметов из n без
учета порядка можно единственным
способом – выбрать все n предметов.)
Следствие 3. При r>n
![]() (в сочетаниях с повторениями r не
может быть больше n, так как мы не
можем из n-множества забрать более,
чем n элементов).
(в сочетаниях с повторениями r не
может быть больше n, так как мы не
можем из n-множества забрать более,
чем n элементов).
Числа
![]() являются коэффициентами бинома Ньютона
(a+b)n:
являются коэффициентами бинома Ньютона
(a+b)n:
![]()
Например, (a+b)3 = a3 + 3a2b + 3ab2 + b3
![]() .
.
Поэтому числа сочетаний без повторений еще называют биномиальными коэффициентами.
Ещё одно обозначение этих чисел:
![]() .
.
Выборка. Виды выборок. Примеры. Неупорядоченные выборки. с повторениями. Доказательство с помощью метода отображений. Следствия. Метод Эйлера.
