ТЕОРИЯ
Дидактический материал к коллоквиуму 1. 1 семестра . Принимает: Клиндухов.
Ответ на Вопрос 1
аксиоматическое) определение действ чисел.
Непустое
множество
={x}
элементов x произвольнойприроды
называется множествомдействительных
чисел, если
выполняются следующие условия:
IНа
множестве
введена операция сложения
элементов, т.е. указан закон, согласно
которому каждой упорядоченнойпаре
элементов x, y
из
поставлен в соответствие элемент из
обозначаемый
x+yй
называемый суммой
элементов x и y
так, что выполняются следующие (аксиомы
сложения) условия:
(1)I
В
существует единственный нейтральный
элемент (называемый нулём при сложении)
такой, что для любого x
выполнено:
x+ = +x=x
(2)I Для каждого x существует единственный элемент из , называемый противоположным элементу x, обозначаемый (-x) и такой, что
x+(-x)=(-x)+x=
(3)I Для любых x, y, z
x+(y+z)=(x+y)+z(ассоциативность)
(4)I Для любых x, y из
x+y=y+x(коммутативность)
II На множестве введена операция умножения элементов, т.е. указан закон, согласовано которому каждойупорядоченнойпаре элементов x, y из поставлен в соответствие элемент из называемый произведениемx наy и обозначаемый xy так, что выполнены следующие условия (аксиомы умножения):
(1)IIВ существует единственный нейтральный элемент (единица при умножении) обозначаемый 1 такой, что для любого x :
x·1=1·x=x
(2)II
Для любого
x
{
} существует единственный элемент из
,
называемый обратным к x и обозначаемый
x-1
такой, что:
x· x-1=x-1·x=1
(3)II Для любыхx, y, z из :
x·(y·z)=(x·y)·z (ассоциативность)
(4)II Для любыхx, y, z из :
x·y=y·x(коммутативность)
Ответ на вопрос 2 Теор о сущ-нии верх/ нижней грани множества.
Теорема 1. (О существовании точной верхней грани у ограниченного сверху числового множества)
Любое непустое ограниченное сверху числовое множество имеет точную верхнюю грань.
Доказательство.
Пусть
X
,
X
и существует В такое, что для любого x
:
x
В.
Рассмотрим множество E всех чисел, ограничивающих множество X сверху.
E
,
так как В
E.
Следовательно, мы имеем два множества
X и E, обладающих свойством:
X , E и для каждого x и для каждого В E x В.
А тогда согласно аксиоме V (полноты и непрерывности) множества действительных чисел существует Во такое, что для любого x и для любого В E
x Во В.
Из
левой части неравенства x
Во
следует, что для любого x
:
x
Во
Во
ограничивает множество X сверху
Во
E.
Из правой части неравенства следует, что для любого В E: Во В, а так как Во E, то Во – наименьшее из чисел, ограничивающих множество X сверху
Во=supX.
Теорема 2. (О существовании точной нижней грани у ограниченного снизу числового множества).
Любое непустое ограниченное снизу числовое множество имеет точную нижнюю грань.
Доказательство.
Пусть
,
и
– ограниченно снизу, то есть существует
А такое, что для любого x
:
А
x.
Рассмотрим
множество X={-x;
x
}.
Тогда для любого -x
:
-x
-А,
то есть множество X ограничено сверху
и согласно теореме 1 существует Во=supX
для
любого x
:
x
Во
-x
-Во
-Во=inf
Ответ на вопрос 3
Определение.
Говорят, что задана числовая последовательность, если указан закон, согласно которому каждому натуральному числу n поставлено в соответствие число xn.
Беск малые -
0=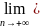
xn
для каждого
>0
существует номер N такой, что для каждого
номера n>N: │xn│<
xn
(-
,
).
Определение.
Последовательность, сходящаяся к нулю, называется бесконечно малой (б.м.).
Последовательность
{xn} называется бесконечно большой, если
(то есть, если
).
Ответ на вопрос 4
Число
а называется
пределом
последовательности (1), если для каждого
положительного числа
>0)
существует натуральное число (номер) N
такое, что для любого номера n>N:
│xn-a│
или
-
<xn-а<
а-
<xn<
xn
(а-
,
а+
)
Определение.
Числовая
последовательность называется сходящейся,
если она имеет предел, то есть если
существует число а
такое, что а=
xn
существует
а
такое, что для каждого
>0
существует номер N такой, что для каждого
номера n>N: │xn-a│
.
Теорема 2.
Любая сходящаяся последовательность ограничена. Обратное неверно.
Определение.
Последовательность называется ограниченной, если она ограничена и сверху и снизу.
Доказательство.
.Пусть {xn} сходится. Докажем, что она ограничена.
{xn}
сходится
существует число а
такое, что для каждого
>0,
а значит и для
=1>0
существует номер N=N(1) такой, что для
любого номера n>N:
│xn-а│< =1 а-1<xn<а+1 xn (а-1, а+1)
положим А=min{x1, x2,…, xN, a-1}
B=max{ x1, x2,…, xN, a+1}
Тогда
для любого
n, n=1, 2, …: А
В.