
Симплекс метод (алгоритм):
1) Зводимо задачу до станд. вигляду, при чому F(x) -> min і “>=”, “=”.
2) Склад. симплекс таблицю. Якщо серед обмеж є рівняння, необх. спочатку замінити 0 в базисі на вільну змінну.
3)Знаходимо допустимий розв’язок. Послідовно застов. Правило 1, до того моменту, покі всі члену будуть невід’ємні. Досягаємо невід’ємності вільних членів або відсутн. допустимої області.
Допустимий розв’язок –розв’язок, який задовольняє сист. обмеж та умову невід’ємн.
Базисний допуст. розв’язок – розв’язок допустимий, з вільними змінними рівними 0.
4)Знаход. оптим розв’язок (за Правилом 2)
Елементи ост. рядка назив. оцінками, x1, x2 – вільні змінні – це змінні, через яккі вираж. інш змінні сис-ми. Базисні змінні – це ті змінні, які вираж. з сист. через вільні змінні.
Для того, щоб знайти оптим. план ЗЛП вільні змінні повинні = 0, щоб потрапити у верш. многогранника. Ознакою оптим. плану. є невід’ємність оцінок.
Правило 2. Для прямув. до оптим. плану беремо віднош. додатніх вільних членів до від’ємн. ел-тів у їх рядках, які належ стовпчикам з від’ємн. оцінками. З усіх таких відн. обираємо найбільше і ел-т, що дає таке віднош. беремо за ведучий.
Зауваження 1. Якщо в процесі пошуку допуст. плану виявл., що у рядку, де є від’ємн. вільний член немає додатн. ел-ів, то задача допустим. плану не має. Економ. зміст: для викон. обсягу робіь не вистачає ресурсів.
Зауваження 2. Якщо в процесі пошуку оптим. плану виявл., що у стовпчику з від’ємн. оцінкою немає дод. елем, то задача не має оптим. плану. ЦФ не обмежена.
Елементи теорії двоїстості
Кожній ЗЛП можна поставити у відповідність іншу здачу ЛП, яку називають двоїстою до даної.
Початкова задача - пряма або вихідна.
Пряма та двоїста задачі тісно пов’язані між собою. З розв’язку однієї можна отримати розв’язок іншої.
Розглянемо загальну ЗЛП:
F(x)
=
 (1)
(1)
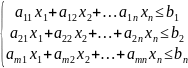 (2)
(2)
 ,
i=
,
i= (3)
(3)
Ф(z)
=
 (4)
(4)
 (5)
(5)
 ,
,
 (6)
(6)
Задача(4)-(6) називається двоїстою до задачі (1)-(3)
Правила побудови взаємодвоїстих задач:
Одна задача повинна бути спрямованою на пошук найбільшого, а інша - найменшого значення цільової функції.
Обмеження задачі на мінімум повинні бути записані за допомогою ≥ і =; а в задачі на максимум – за допомогою ≤ і =.
Кількість змінних однієї задачі повинна бути такою самою як загальна кількість рівнянь та обмежень в системі іншої.
В кожній нерівності системи обмежень однієї задачі повинна відповідати невід’ємна змінна іншої задачі, а кожному рівнянню – змінна на знак якої обмежень не накладено.
Коефіцієнти цільової функції однієї задачі повинні бути вільними членами системи обмежень іншої.
Матриця коефіцієнтів системи обмежень однієї задачі повинна бути транспонованою матрицею коефіцієнтів системи обмежень іншої задачі.
Теорема(основна нерівність теорії двоїстості)
Для будь-яких
допустимих розв’язків прямої задачі
 ={
={
 } та двоїстої
} та двоїстої

справедлива нерівність:
 (7)
(7)
Теорема
Якщо
 та
та
 допустимі плани взаємодвоїстих задач
та значення F(
)
= Ф(
)
(8)
допустимі плани взаємодвоїстих задач
та значення F(
)
= Ф(
)
(8)
то та – оптимальні плани цих задач.
Мала теорема теорії двоїстості
Якщо одна із задач двоїстої пари має оптимальний розв’язок, то його має й інша задача, при чому екстремальні значення цільових функцій збігаються.
Якщо ж цільова функція однієї з задач – необмежена, то інша задача не має допустимого плану.
Економічне значення теореми
В оптимальному для обох задач розв’язку сума виручки дорівнює (F(x)) сумі виручки від продажу ресурсів (Ф(z))
Якщо цільова функція прямої задачі не обмежена, то не знайдеться таких цін, які б скомпенсували нескінченне значення (F(x)).
Двоїстий симплекс метод
Для
розв’язання пари двоїстих задач,
достатньо розв’язати одну з них: якщо
розв’язана перша задача і вона має
оптимальний розв’язок, то оптимальне
значення змінних прямої задачі шукаємо
в стовпчику вільних членів, а оптимальне
значення двоїстої задачі шукають в
рядку оцінок в оптимальному плані
прямої задачі з врахуванням відповідностей
 ;
;
 (9)
(9)
Якщо розв’язали двоїсту задачу, то її розв’язки є вільними членами останньої таблиці, а розв’язки прямої задачі є оцінками змінних відповідно співвідношенню (9)
Якщо змінна двоїстої задачі залишилася у базисі, то відповідна їй змінна прямої задачі є вільною і дорівнює 0.
