2. Вариация коэффициентов цф
Пусть R(c) – задача ЛП, ограничения совпадают с ограничениями задачи P , ЦФ имеет вид f (c;x) = c · x.
Определение: Множество всех векторов c таких, что является решением задачи R(c), назовем областью постоянства оптимального решения (ОПОР).
Графически для прямой задачи – решение остается неизменным при изменении коэффициентов ЦФ, когда изменяется ее градиент (происходит поворот целевой функции вокруг оптимальной точки).
Определение:
Пусть β
– произвольный базис матрицы A0,
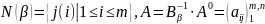 .
Для любого
.
Для любого
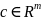 положим
положим
 .
.
Утверждение:
Вектор
принадлежит ОПОР, если и только если
существует оптимальный в задаче R(c)
базис β
матрицы A0,
для которого
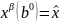 .
.
Определение:
Множество
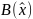 – это множество всех базисов β
матрицы A0
таких, что
.
– это множество всех базисов β
матрицы A0
таких, что
.
Для
каждого
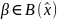 положим
положим
 .
.
Следствие
(общее описание ОПОР):
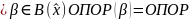 .
.
Зафиксируем .
Зная
базисную матрицу
,
найдем матрицу
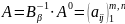 .
.
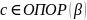 эквивалентно
эквивалентно
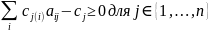 (**).
(**).
После
приведения задачи R(c)
(или P)
к базису
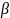 условия (**) для базисной части полностью
выполнены. Достаточно рассмотреть эти
условия для небазисной компоненты
условия (**) для базисной части полностью
выполнены. Достаточно рассмотреть эти
условия для небазисной компоненты
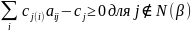
Пусть
вектор
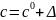 ,
где
,
где
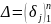 .
Тогда условие (**) запишется следующим
образом:
.
Тогда условие (**) запишется следующим
образом:
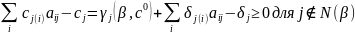
Эту
систему чаще всего рассматривают для
найденного оптимального базиса
,
описывая таким образом
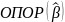 .
.
Утверждение: Если – невырожденное решение задачи P,
то
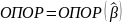 .
.
Обозначим
для разрешимой задачи R(c)
через
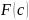 – оптимальное значение ЦФ. Кроме того,
для всякого базиса β
матрицы A0
и любого вектора
положим
– оптимальное значение ЦФ. Кроме того,
для всякого базиса β
матрицы A0
и любого вектора
положим
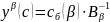 .
.
Свойства векторов ОПОР:
Если
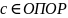 ,
то
является решением задачи R(c);
,
то
является решением задачи R(c);Если , то
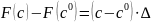 ;
;Если , то
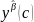 есть вектор двойственных оценок для
задачи R(c).
есть вектор двойственных оценок для
задачи R(c).
Прогноз максимального значения ЦФ
Пусть , где .
Вычислим
матрицу
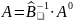 и
и
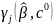 для всех j.
для всех j.
Если неравенства
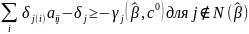
выполняются,
то
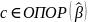 и вектор
оптимален в обеих задачах P
и R(c),
поэтому
и вектор
оптимален в обеих задачах P
и R(c),
поэтому
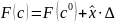 .
.
Если неравенства не выполняются, то исследователю проще решить новую задачу.
Прогноз двойственных оценок
Двойственные оценки отражают относительную полезность ингредиентов.
Утверждение:
Если
и
,
то вектор
 является решением задачи R*(c).
В частности, при
является решением задачи R*(c).
В частности, при
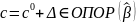 решением задачи является вектор
решением задачи является вектор
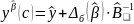 .
.
Частный случай: вариация одного коэффициента ЦФ
Пусть изменяется только одна компонента вектора (с номером k):
и .
Тогда неравенства перепишутся следующим образом
.
Рассмотрим 2 случая.
1)
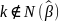 .
Тогда
.
Тогда
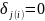 для всех базисных компонент.
для всех базисных компонент.
Для
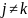 и
неравенство принимает вид
и
неравенство принимает вид
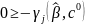 и оно всегда выполняется, так как все
неотрицательны.
и оно всегда выполняется, так как все
неотрицательны.
При
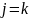 получаем
получаем
 или
или
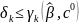 .
.
Следовательно,
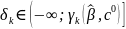 .
.
2)
 .
Пусть
.
Пусть
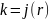 .
Тогда
.
Тогда
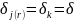 и
и
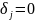 для всех
.
Поэтому неравенства перепишутся в виде
для всех
.
Поэтому неравенства перепишутся в виде
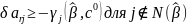 .
.
Это система линейных неравенств относительно одной переменной .
Если
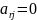 ,
то соответствующее неравенство
выполняется при любом
.
Если
,
то соответствующее неравенство
выполняется при любом
.
Если
 ,
то, разделив неравенства на него, получим
нижнюю неположительную границу для
.
,
то, разделив неравенства на него, получим
нижнюю неположительную границу для
.
Если , то аналогичным образом получим верхнюю неотрицательную границу.
Вектор двойственных оценок вычислим следующим образом
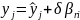 ,
,
где
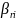 – элементы матрицы
– элементы матрицы